「Maxima」を活用して数学の学習ロードを駆け抜けよう!
(注) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
| ■ 数式処理ソフト「Maxima」を活用した数学学習 [Map] |
|
| ||||
|
| ||||
| [御案内] 「Maxima」(マキシマ)は,フリーの数式処理ソフトです. 有料の Mathematica や Maple に劣らないレベルの数式処理が可能であり, Linux,Windows,MacOSのみならず,Android版もあります. ここでは,数学学習での Maxima の活用法について解説します. | ||||
|
[お知らせ] スマホ(Android)版Maximaの解説本を出版しました. 計算問題やグラフの確認をするときに非常に重宝します. フリーソフトなので一度試してみてください. PC版のコマンドレファランスとしても利用できます。
| ||||
|
| ||||
| ■数学学習での活用 |
|
|
以下では,「TeXmacs」+「Maxima」の画面で基本的な使い方を解説します. |
| 確率・統計 |
| 統計に特化したソフトウェアとしては,SPSS,SAS,Rなどが有名ですが, Maximaにも統計向けのパッケージが備わっています. |
|
|
|
■いろいろな確率分布 |
いろいろな統計解析を行うには,
特定の統計量がどのような分布をするのかが重要です.
Maximaは下記のように多様な分布を扱うことができます.
世の中の多くのことは、
「正規分布」ではなく「ベキ分布」に従っているようです。
「ベキ分布:リンク集」も参照してください。
確率分布に関するパッケージ「distrib」を読み込むと, 確率密度関数,分布関数,分布関数の逆関数,平均,分散,標準偏差,歪度係数, 尖度係数,乱数などを個々の確率分布ごとに求めることができます. 詳細は,マニュアルの「52.distrib」を参照してください. |
|
安定分布 確率分布の分類の中で, 正規分布やコーシー分布を含む「安定分布」というものがあります. この確率分布を説明するにはフーリエ変換の知識を必要とするので 通常の教科書で触れられることは少ないのですが, 現実の世界では正規分布以上に重要な確率分布であるようです. ここでは,私の理解の範囲内での解説を試みたいと思います. 計算違いや認識違いがあるときはご指摘いただけるとありがたいです. |
|
安定分布の定義 同一の確率分布(平均 \(\small \mu\),分散 \(\small \sigma^2\)) にしたがう互いに独立な確率変数を \(\small X_1,X_2,\ldots,X_n\) として 標本平均を \(\small \bar{X}\) とすると, 中心極限定理は, \(\small n\to\infty\) のとき \(\small (\bar{X}-\mu)/(\sigma/\sqrt{n})\) は標準正規分布に収束する ことを述べています. これは,標準正規分布 \(\small N(0,1)\) にしたがう確率変数を \(\small Z\) として, \(\small n\to \infty\) のとき分布が一致することを 「\(\small \overset{d}{=}\)」で表すことにすると, \[\small \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\overset{d}{=} Z\] ということです.この式は \(\small \bar{X}=\frac1{n}(X_1+X_2+\cdots+X_n)\) であることから \[\begin{align*}\small \bar{X}&\small -\mu\overset{d}{=}\frac{\sigma}{\sqrt{n}}Z\\ \small X_1+X_2+&\small \cdots+X_n\\ &\small \quad \overset{d}{=}\sqrt{n}\sigma Z+n\mu\end{align*}\] と表すことができます. さらに,\(\small X\) も \(\small X_i\) と同じ確率分布にしたがう確率変数とすると,それを標準化した \[\small Z=\frac{X-\mu}{\sigma}\] は標準正規分布にしたがいます.この式は \[\small X=\sigma Z+\mu\] と表されるので, \[\begin{align*} \small \sqrt{n}\sigma Z+n\mu &\small =\sqrt{n}(X-\mu)+n\mu\\ &\small =\sqrt{n}X+(n-\sqrt{n})\mu \end{align*}\] となり,\(\small X_i\) の和は \[\begin{align*} \small X_1+X_2+ &\small \cdots+X_n\\ &\small \overset{d}{=}\sqrt{n}X+(n-\sqrt{n})\mu \end{align*}\] と表されます. これは,同一の確率分布にしたがう独立な確率変数の和が 同じ分布にしたがう確率変数の1次式で表される分布に近づくことを 示しています.右辺には分散が含まれず,平均と標本数だけを 含む式になっています. 平均が存在しないような確率分布の一つの範疇に「 安定分布」というものがあります. ある確率分布にしたがう確率変数 \(\small X\) の独立なコピーを \(\small X_1, X_2, \ldots\) とします. \[\begin{align*} \small X_1+X_2&\small +\cdots+X_n\\ &\small \quad \overset{d}{=}c_nX+d_n \end{align*}\] となる定数 \(\small c_n, d_n\) が存在するとき, 確率変数 \(\small X\) は安定であるといいます. \(\small d_n=0\) のときは「厳密に安定である」といわれます. 安定分布では,同じ分布にしたがう独立な確率変数の和の分布が, 同じ分布にしたがう確率変数の1次式の分布と一致するということです. 安定であれば,これから述べる 特性関数 のパラメーターの一つである \(\small \alpha\) を用いて \(\small c_n=n^{\frac1{\alpha}}\) と表されます. そこでは,平均や分散の存在は仮定されません. 正規分布もコーシー分布も安定分布であることが知られています. つまり,「安定分布」は,平均や分散が存在する正規分布や, それらがいずれも存在しないコーシー分布をも含む, より広い範疇の確率分布といえます. |
|
|
|
特性関数 安定分布は,その 確率密度関数をフーリエ変換した関数で 特徴付けられます.その関数を特性関数といいます。 通常,関数 \(\small f(x)\) のフーリエ変換は,Maximaでは \[\small \hat{f}(t)=\frac1{\pi}\int_{-\infty}^{\infty}f(x)e^{-itx}\,dx\] で定義され,その逆変換は \[\small f(x)=\frac12\int_{-\infty}^{\infty}\hat{f}(t)e^{itx}\,dt\] としていますが,確率論ではこれを逆にして, フーリエ変換を \[\small \hat{f}(t)=\int_{-\infty}^{\infty}f(x)e^{itx}\,dx\] で定義し,逆変換は \[\small f(x)=\frac1{2\pi}\int_{-\infty}^{\infty}\hat{f}(t)e^{-itx}\,dt\] で考えるようです.積分範囲が \(\small (-\infty,\infty)\) なので 符号の違いは本質的ではありません. 逆にして考えるのは, 確率密度関数を \(\small f(x)\) としたとき, \(\small \hat{f}(t)\) は \(\small e^{itx}\) の 平均とみることができるからと思われます. 安定分布の特性関数 \(\small \varphi(t)\) は,ちょっと複雑ですが 次の式で表されます. つまり,分布が安定分布であるための必要十分条件は, その特性関数が次の式で表されることです. \[\small \exp\left\{ i\delta t-\gamma^{\alpha}|t|^{\alpha}\left\{1+i\beta {\rm sgn}(t) \omega(t,\alpha)\right\}\right\}\] ここで,それぞれのパラメーターは,次のような意味を持ちます. 特に,\(\small \alpha\) を特性指数といいます. \(\small i\) は虚数単位, \(\small 0\lt \alpha\leq 2\),\(\small -1\leq\beta\leq 1\), \(\small 0\lt\gamma\lt \infty\), \(\small -\infty\lt\delta\lt\infty\), \(\small {\rm sgn}\,(t)\) は符号関数, \(\small \omega(t,\alpha)\) は次式で定義される. \[\small \omega(t,\alpha)=\begin{cases}\tan\frac{\pi\alpha}{2} &(\alpha\neq 1)\\ \frac2{\pi}\log(|t|)&(\alpha=1)\end{cases}\]
ただし,安定分布の特性関数にはいろいろな定義の仕方があるようです.
私自身も参照先で異なる式が書かれていて,どちらが正しいのだろうかと
悩んでしまいました.10種類以上の定義の仕方があるようです.
上記の定義は文献等で最もよく利用されている定義のようです.
一方では数値計算で利用しやすいタイプの式もあり,
「複数の定義が混在するのは避けられない」ようです.
[参照(p.2)].
|
|
|
|
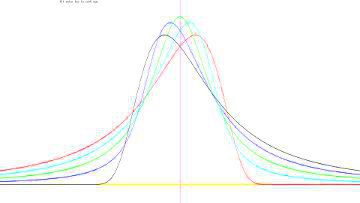
グラフの比較 以下の分布は, 安定分布の中で確率密度関数を具体的な式で表すことのできる例として重要です. 安定分布で確率密度関数を式で表すことができるのは, この3種類の分布だけのようです. \(\small \alpha\) の値の違いに留意して下さい.
(%i13)のべき分布(パレート分布)は, グラフに合わせて左に平行移動する形で求めています. Maximaにはレビ分布は登録されていないので,(%i14)では 累積分布関数を定義しています.広義積分になるので 「ldefint」で定義しました. (%i18)と(%o18)の間には,実際には小数をどのような有理数に 置きかえたかのメッセージが表示されます. その部分は省略しました. 下図は,結果をグラフ化したものです. |
|
|
|
確率密度関数 安定分布 \(\small S(\alpha,\beta,\delta,\gamma)\) は 特性関数のパラメーターの値で定義されます. 特に,\(\small \alpha\) の値が重要であり,安定分布になるのは \(\small 0\lt \alpha\leq 2\) であるときに限ります. 特性関数をフーリエ逆変換すれば確率密度関数が求められるはずですが, きちんと式で表現できるのは正規分布,コーシー分布,そしてレビ分布の 場合だけであるようです. ここで,特性関数を フーリエ逆変換すると確率密度関数が得られることを, 実際の計算で確認してみましょう. 1.標準正規分布N(0,1)は,安定分布 \(\small S(2,0,\frac1{\sqrt{2}},0)\) と対応するので,特性関数は下記の関数です. \[\small \varphi(t)=e^{-\frac{t^2}{2}}\] 確率密度関数は,次の式を計算することで得られます. \[\begin{align*} \small \frac1{2\pi}\int_{-\infty}^{\infty} &\small \varphi(t)e^{-itx}\,dt\\ &\small =\frac1{2\pi}\int_{-\infty}^{\infty}e^{-\frac{t^2}{2}}e^{-itx}\,dt\\ &\small =\frac1{2\pi}\int_{-\infty}^{\infty}\left(e^{-\frac{t^2}{2}}\cos{tx}\right.\\ &\small \qquad \left.-ie^{-\frac{t^2}{2}}\sin{tx}\right)\,dt\\ &\small =\frac1{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \end{align*}\] ここで,実際の積分計算はMaximaを利用しました. 2.コーシー分布 Cauchy(1,0) の場合は, 安定分布 \(\small S(1,0,1,0)\) に対応します. 特性関数は \[\small \varphi(t)=\exp(-|t|)\] となるので,確率密度関数は次により計算されます. \[\begin{align*} \small \frac1{2\pi}\int_{-\infty}^{\infty} &\small e^{-|t|}e^{-itx}\,dt\\ &\small =\frac1{2\pi}\int_{-\infty}^{\infty}\left(e^{-|t|}\cos{tx}\right.\\ &\small \qquad \left.-ie^{-|t|}\sin{tx}\right)\,dt\\ &\small =\frac1{\pi(1+x^2)} \end{align*}\] ここでも,積分計算にはMaximaを利用しました. |
|
|
|
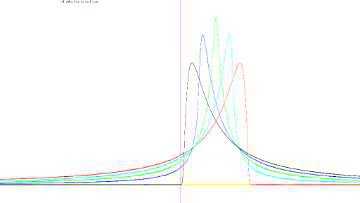
平均の分布 分散が存在する確率分布では, 中心極限定理により標本平均は正規分布に近づいていきます. 安定分布ではどのようになっているかを確認してみましょう. 安定分布の定義によれば,元の分布と同じような分布に近づいていくはずです.
■正規分布の場合 以上のもとで,(%i43)では「Lnor」の区間 \(\small [-5,5]\) を 50等分したときの度数分布を作成しています. 5個の標本平均を取ると標本平均は原点の回りに集まってくるので, この範囲を超えるものは無くエラーは生じませんでした. (%i44)は,グラフを描く場合の対応する \(\small x\) 軸の分点リストです. (%i45)では,N(0,1)の確率密度関数も表示しています. |
|
|
|
■コーシー分布の場合 この場合もすでに表示済みですが, ここではヒストグラムを折れ線グラフ として作成してみましょう. 以下では,wxMaximaを使用します. 「distrib」と「descriptive」は読み込み済みです. 次に,10個の標本平均の場合も同様にして作成し, 下記の(%i33)によりグラフを描画します. |
|
|
|
■べき分布の場合 ベキ分布(パレート分布)の場合に,同様のことを確かめてみましょう. |
|
|
|
■レビ分布の場合 レビ分布についての平均の比較は, 「レビ分布」を参照してください. |
|
|
|
安定分布の性質 安定分布は,正規分布やコーシー分布・レビ分布を含む 広い範疇の確率分布であり,確率密度関数を フーリエ変換した特性関数で特徴づけられます. 世の中のいろいろな事象が「べき乗則」に従っていることが明らかになるにつれ, この「安定分布」の重要性が高まっています. しかしながら,この分布について詳しく解説している和書は, Web検索しても見つけることができませんでした. 英文検索すると, リンク集にも収録した下記のサイトが比較的分かりやすいように思います.
■定義
■基本的性質 [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15], [16], [17], [18], [19], [20], [21], [22] |
|
|
|
[2] 安定分布 \(\small X\) が平均 \(\small \mu\) と
分散 \(\small \sigma^2\) を持てば,
\(\small a_n=(n-\sqrt{n})\mu, b_n=\sqrt{n}\) である.
(証明) \(\small X_i~(1\leq i\leq n)\) は互いに独立なので, \(\small X_1+X_2+\cdots+X_n\) の平均は \(\small n\mu\) , 分散は \(\small n\sigma^2\) である.また,\(\small a_n+b_nX \) の 平均は \(\small a_n+b_n\mu\),分散は \(\small b_n^2\sigma^2\) である. \(\small X\) は安定分布で両者の平均と分散は一致するから \[\small n\sigma^2=b_n^2\sigma^2\quad \therefore\quad b_n=\sqrt{n}\] \[\small n\mu=a_n+b_n\mu\quad \therefore\quad a_n=(n-\sqrt{n})\mu\] したがって,この場合は \[\begin{align*} \small X_1+X_n&+\small \cdots+X_n\\ &\small \overset{d}{=}(n-\sqrt{n})\mu+\sqrt{n} X \end{align*}\] \[\begin{gather*}\small (X_1+\cdots+X_n)-n\mu\overset{d}{=}\sqrt{n}(X-\mu)\\ \small \bar{X}-\mu\overset{d}{=}\frac{X-\mu}{\sqrt{n}}\\ \small \therefore\quad \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\overset{d}{=}\frac{X-\mu}{\sigma} \end{gather*}\] となります. この式から, 平均と分散が存在するような安定分布にしたがう標本平均の標準化は, もとの安定分布の標準化と同じ分布にしたがうことが分かります.
[3] \(\small X\) が安定であれば,
\(\small Y=c+dX\) も安定で,
\(\small Y\) の中心化定数は \(\small da_n+(n-b_n)c\),
規格化定数は \(\small b_n\) である.
ただし,\(\small c\) は実数,\(\small d\) は正の実数とする.
[4] \(\small X\) が安定であれば,\(\small -X\) も安定で,
中心化定数は \(\small -c_n\),規格化定数は \(\small b_n\)
である.
[5] \(\small X, Y\) が安定で,
\(\small Y\) は \(\small X\) と同じ規格化定数\(\small b_n\)を持ち、
中心化定数は \(\small c_n\) とする. このとき,
\(\small Z=X+Y\) は安定で,
中心化定数 \(\small a_n+c_n\), 規格化定数 \(\small b_n\) を持つ.
|
|
|
|
[6] \(\small X\) が安定であるための必要十分条件は,
\(\small X_1, X_2\) を同じ分布にしたがう独立な確率変数とするとき,
正の実数 \(\small d_1, d_2\) に対して \(\small d_1X_1+d_2X_2\) が
\(\small a+bX\) と同じ分布にしたがうことである.
ただし,\(\small a\) は実数,\(\small b\) は正の実数である.
(証明) \(\small n (\geq 2)\) に関する数学的帰納法で考えます. (i) \(\small n=2\) のとき, \(\small X\) が安定であれば, つまり [1] が成り立てば,[3]より \(\small d_1X_1, d_2X_2\) も 規格化定数が \(\small X\) と同じ安定分布です. すると,[5]より \(\small d_1X_1+d_2X_2\) も規格化定数が \(\small X\) と 同じ安定分布になるので,\(\small d_1X_1+d_2X_2\) は \(\small a+bX\) と同じ分布にしたがいます. 逆に,\(\small d_1X_1+d_2X_2\) が \(\small a+bX\) と同じ分布にしたがえば,それは [1] の定義で \(\small d_1=d_2=1\) の場合が成り立つことになるので, \(\small X\) は安定です. (ii) \(\small n\) のとき成り立ったと仮定して, \(\small X_1+X_2+\cdots+X_{n+1}\) の分布を考えます. \(\small Y_n=X_1+\cdots+X_n\) とおくと, 帰納法の仮定により \(\small Y_n\) は \(\small a_n+b_nX_1\) と 同じ分布にしたがうので, \(\small Y_n+X_{n+1}\) は \(\small a_n+b_nX_1+X_{n+1}\) と 同じ分布にしたがいます.[3]より \(\small b_nX_1\) は \(\small X\) と 同じ分布にしたがうので,[5]により \(\small b_nX_1+X_{n+1}\) も \(\small X\) と同じ分布にしたがい, \(\small b_nX_1+X_{n+1}\overset{d}{=}c+b_{n+1}X\) の形で表せます. したがって, \[\small X_1+\cdots+X_{n+1}\overset{d}{=}(a_n+c)+b_{n+1}X\] となり,\(\small n+1\) のときも安定になります.
[7] \(\small X, Y\) が同じ安定分布にしたがい互いに独立であれば,
\(\small X-Y\) は厳密に安定で同じ規格化定数を持つ.
[8] \(\small X\) が安定であれば,規格化定数は
\(\small 0\lt \alpha \leq 2\) となる\(\small \alpha\) に対して
\(\small b_n=n^{\frac1{\alpha}}\) と表せる.
\(\small \alpha\) を特性指数という.
[9] すべての安定分布は連続分布である.
[10] \(\small X_1,X_2,\ldots\) を同一の確率分布にしたがう
独立な確率変数とし,\(\small Y_n=\sum_{i=1}^{n}X_i\) とする.
\(\small n\to\infty\) のとき
\[\small \frac{Y_n-a_n}{b_n}\]
が収束するような定数 \(\small a_n, b_n~(b_n>0)\) が存在すれば,
収束先の分布は安定分布である.
|
|
|
|
[11] 確率変数 \(\small X\) は安定であるとすると,
\(\small X\) の特性関数 \(\small E(e^{itX})\) は
\(\small 0\lt \alpha\leq 2\),\(\small -1\leq \beta\leq 1\),
\(\small 0\lt \gamma \lt \infty\),\(\small -\infty\lt \delta\lt \infty\) とするとき,
次の式で表される.
\[\small
\exp\left(i\delta t-\gamma^{\alpha}|t|^{\alpha}\left\{1+i\beta
{\rm sgn} (t)\omega(t,\alpha)\right\}\right)\]
ここで,\(\small {\rm sgn}\) は符号関数で,
\(\small \omega(t,\alpha)\) は次の式で定義されます.
\[\small
\omega(t,\alpha)=\begin{cases}\tan\left(\frac{\pi\alpha}{2}\right)
&(\alpha\neq 1)\\ \frac2{\pi}\log(|t|)&(\alpha=1)\end{cases}\]
\(\small \alpha\) は特性指数で,
\(\small \beta\) は歪度,
\(\small \gamma\) は分布のスケール,
そして \(\small \delta\) は分布の位置を定める定数である.
特に,\(\small \gamma=1, \delta=0\) のときの特性関数は次のようになる. これを,安定分布の標準形という. \[\small \exp(-|t|^{\alpha}\left\{1+i\beta {\rm sgn}(t) \omega(t,\alpha)\right\})\] なお,文献「2」では \(\small \gamma, \delta\) が \(\small d, c\) を用いて 表されているが,ここでは特性関数の 箇所の式に合わせて \(\small \gamma,\delta\) を使用した式で示した.
[12] 確率変数 \(\small X_1, X_2\) は互いに独立で,
同じ特性指数 \(\small \alpha\) をもつ安定分布にしたがうものとし,
[11]の他の定数をそれぞれ \(\small \beta_i, \gamma_i, \delta_i (i=1,2)\) とする.
このとき,\(\small X_1+X_2\) は特性指数 \(\small \alpha\)
を持つ安定分布で,[11]の他の定数は
\(\small \delta=\delta_1+\delta_2\),
\(\small \gamma=(\gamma_1^{\alpha}+\gamma_2^{\alpha})^{\frac1{\alpha}}\),
そして
\[\small \beta=\frac{\beta_1\gamma_1^{\alpha}+\beta_2\gamma_2^{\alpha}}
{\gamma_1^{\alpha}+\gamma_2^{\alpha}}\]
である.
[13] 標準正規分布 N(0,1) は,
特性指数が \(\small \alpha=2, \gamma=1/\sqrt{2}\) の安定分布である.
[14] コーシー分布 Cauchy(0,1) は安定分布で,特性指数は \(\small \alpha=1\) で \(\small \beta=0\) である. [15] レビ分布 Levy(0,1) は安定分布で, 特性指数は \(\small \alpha=\frac12\) で \(\small \beta=1\) である. |
|
|
|
[16] 安定分布の確率密度曲線には単峰性(unimodal)がある.
つまり,「グラフに一つの盛り上がりがある」ということです.
実際,正規分布・コーシー分布・レビ分布とも,一つの山ができています.
[17] 安定分布 \(\small S(\alpha,-\beta,\gamma,\delta)\) の確率密度曲線は,\(\small S(\alpha,\beta,\gamma,\delta)\) の確率密度曲線を 反転させたものである. [18] 安定分布 \(\small S(\alpha,\beta,\gamma,\delta)\) において, \(\small \alpha\) が小さいと歪度が大きく, 大きいと歪度が小さい(p4).実際, 正規分布・コーシー分布・レビ分布では \(\alpha=2,1,0.5\) ですが,グラフはこの順番で歪度が大きくなっています. [19] 安定分布 \(\small S(\alpha,\beta,\gamma,\delta)\) の確率密度関数の定義域は実数全体か半直線であり, 半直線になるのは \(\small 0\lt \alpha\lt 1, \beta=\pm1\) の ときに限る.具体的には, \(\small \beta=1\) のときは \(\small [\delta,\infty)]\), \(\small \beta=-1\) のときは \(\small (-\infty,\delta]\).
[20] 安定分布 \(\small S(\alpha,\beta,\gamma,\delta)\) は,
\(\small \alpha=2\) の正規分布のときは裾が軽く(light tail),
全てのモーメントが存在する.しかし,
それ以外では裾が重く(heavy tail),漸近的にべき乗で減少する.
\(\small \alpha\lt 2\) のときは,正規分布と区別するため
「安定パレート分布」という.
[21] 安定分布 \(\small S(\alpha,\beta,\gamma,\delta)\) において, \(\small \alpha\lt 2\) であれば分散は存在しない. さらに,\(\small \alpha\leq 1\) であれば平均が存在しない. 分数モーメントを使用するとき,\(\small E(|X|^p)\) は \(\small 0\lt{p}\lt\alpha\) であるときに限り存在する. [22] それぞれの特性指数 \(\small \alpha\) が異なる安定分布にしたがう 確率変数を \(\small X, Y\) とすると, \(\small X+Y\) は安定ではない. |
|
|
|
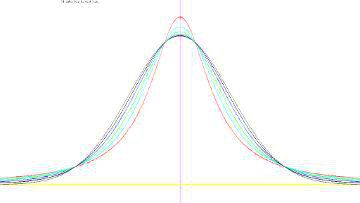
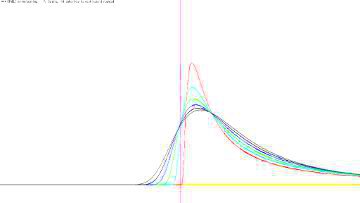
4つのパラメーター 安定分布 \(\small S(\alpha,\beta,\gamma,\delta)\) は, 次の特性関数を表す4つのパラメーターで規定されます. \[\small \exp\left\{ i\delta t-\gamma^{\alpha}|t|^{\alpha}\left\{1+i\beta {\rm sgn}(t) \omega(t,\alpha)\right\}\right\}\] ここで,\(\small i\) は虚数単位, \(\small 0\lt \alpha\leq 2\),\(\small -1\leq\beta\leq 1\), \(\small 0\lt\gamma\lt \infty\), \(\small -\infty\lt\delta\lt\infty\), \(\small {\rm sgn}\,(t)\) は符号関数, \(\small \omega(t,\alpha)\) は次式で定義される. \[\small \omega(t,\alpha)=\begin{cases}\tan\frac{\pi\alpha}{2} &(\alpha\neq 1)\\ \frac2{\pi}\log(|t|)&(\alpha=1)\end{cases}\] この関数をフーリエ逆変換すると確率密度関数が得られますが, それを具体的な式で表すことができるのは正規分布・コーシー分布・レビ分布の 3つの場合に限られます.それらの特性指数は, それぞれ \(\small \alpha=2, 1, 0.5\) です. 4つのパラメーターの意味を把握するには, これ以外の分布の確率密度関数がどのようなグラフになるかを知りたいところです. 確率密度関数を式で表すことができる3つの分布の式をみると, \(\small \gamma\) は分布の大きさ(要するに縦方向の変化)を定め, \(\small \delta\) は分布の位置(要するに平行移動)を定めるパラメータに なっていることが分かります.したがって, \(\small \alpha, \beta\) の値によりグラフがどのように違ってくるかを 知りたいところです. 実は,\(\small \alpha=\frac23, \frac32\) の場合は, その確率密度関数を超幾何関数を用いて表すことができるようです. 詳しくは「こちら」 (「R」での解説)を参照してください.
ここに,安定分布の性質の箇所で参照した
文献2の著者
John P. Nolan 教授 (ワシントン州,アメリカン大学) による
安定分布をシミュレートできる「stable.exe」というプログラムがあります.
パラメーターを指定することで,確率密度曲線(pdf),累積分布曲線(cdf),
累積分布関数の逆関数(quantile),乱数の生成などを行うことができます.
■ \(\small S(2,\beta,1,0)\) の場合
■ \(\small S(1,\beta,1,0)\) の場合
■ \(\small S(0.5,\beta,1,1)\) の場合
■ \(\small S(\alpha,0,1,0)\) の場合
■ \(\small S(\alpha,1,1,1)\) の場合
|
|
|
|
リンク集 「べき分布」「安定分布」「レビ分布」の項目を作成するにおいては, 下記のサイトを参照させていただきました. |
|
■べき分布・パレートの法則・ジップの法則 |
| ■ベキ分布に関する解説 |
|
| ■ベキ分布が利用されている論文 |
|
|
|
| ■Tsallis統計力学 |
| ■安定分布・レビ分布・コーシー分布 |
|
| ■中心極限定理 |
| ■複雑系ネットワーク |
|
|
■ネットワーク描画ソフト「Pajek」 ネットワークを描画するフリーソフトです. 下記の最初のサイトからファイルをダウンロードできます. |
|
| ■英文サイト |
|
|
|