gnuplotを利用してグラフの作成ロードを駆け抜けよう!
(注) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
| ■ 「gnuplot」によるグラフの作成 [Map] |
|
| ||
|
| ||
|
[御案内] TeXを利用した数学プリントの作成では,
関数のグラフをどのように作成するかは大きな問題です.
ここでは,フリーのグラフ描画ソフト「gnuplot」を用いた
グラフの描画方法とTeXへの取り入れ方について解説します.gnuplotは,
数式処理ソフトMaximaにも組み込まれているソフトです.
離散的な実験データのグラフ化や2変数関数のグラフも描画することができ,
理工系の研究論文の図の作成にも利用されています.
C言語で作成された関数ライブラリーGSLを利用することもできます.
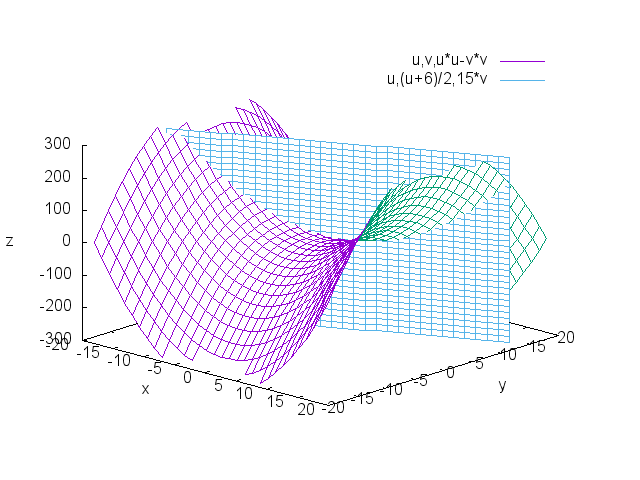
なお,関数のグラフ描画ソフトとしては,gnuplotの他に下記のようなソフトもあります. WinTpic, Ngraph, GRAPES, FunctionView, GeoGebra, Cinderella ★gnuplotを利用しなくても、TeXの中でMetaPostを利用して 立体図形や曲面描画を可能にする「MePoTeX」というマクロパッケージがあります。 その解説ページを作成したので、 TeXを利用している方は参照してください。たとえば、 下記のような図をTeXのソースコードの中に簡単に記述でき、 パラパラ漫画まで作成することができます[概要1、概要2]。最後のグラフは、球面調和関数のグラフです [概要]。 ★このページには数学絡みで訪れる方が多いと思われますが、
| ||
|
[お知らせ] 下記を出版しました。 PCやスマホで使える数式処理ソフト Maximaの解説書です。 計算問題やグラフ問題の解答を作るときに非常に重宝します。 フリーソフトなので一度試してみてください。 なお、Maximaでのグラフ描画ではgnuplotが利用されています。 PC版Maximaでグラフを描いてeps保存すれば、 数学のプリント作成の際にも利用することができます。
| ||
|
|
| ■「gnuplot」とは? |
|
|
| 「gnuplot」とは? |
|
gnuplotは
1変数や2変数の関数のグラフを描画するフリーのアプリケーションで,
Unix, Windows, MacOS, Androidなど多数のOS上で動作します.
「グニュープロット」と呼ばれることもありますが,
本来は「ニュープロット」と呼ぶようです.
「gnu」がついていますが,
「GNUプロジェクト」とは関係しないフリーソフトです.
描画されたグラフをファイル保存(eps, pdf, jpeg等)すると,
TeXのファイルとして取り入れることができます.
このページでは,gnuplotによる基本的なグラフの描画方法と, TeXのファイルとしての取り入れ方について解説します. 細かい使い方は,他の解説サイトを参照してください. とりあえず,どのようなグラフが表示できるかは下記のサイトを参照してください. gnuplotによる多数の出力例が紹介されています.
|
| ダウンロード |
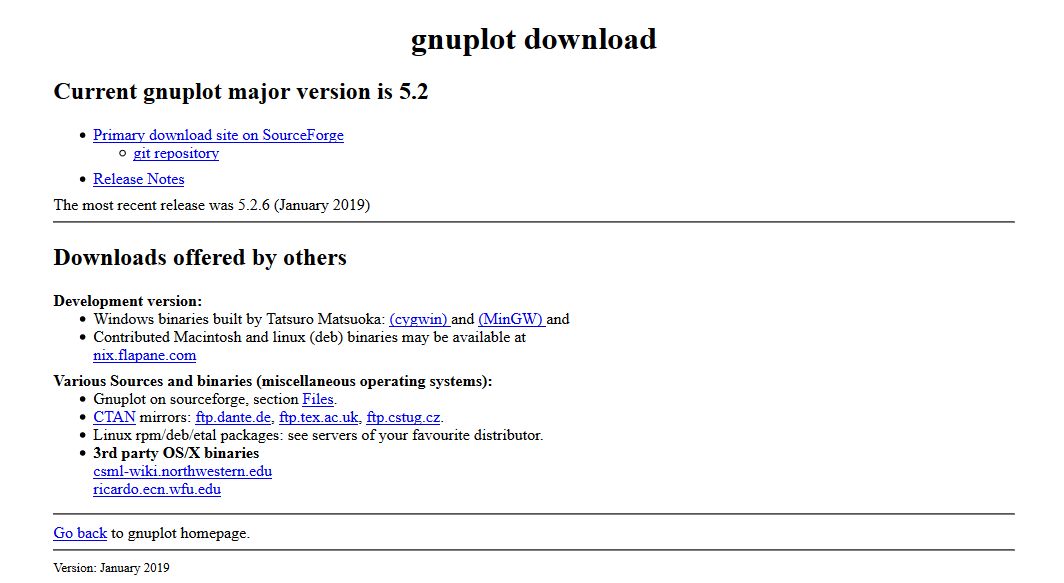
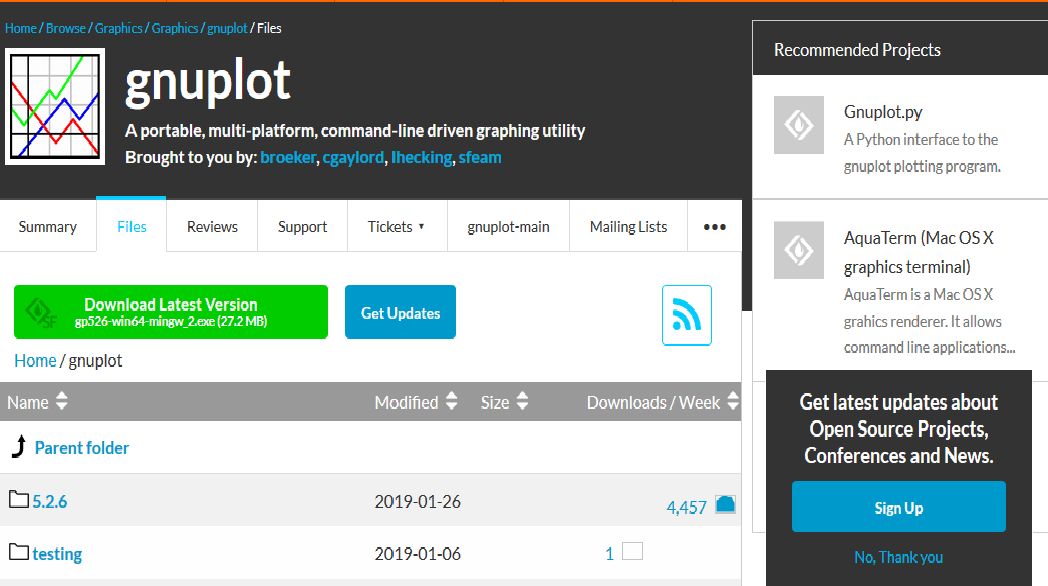
最初に,次の手順でgnuplotの最新版をダウンロードします.
以下は,ダウンロードの主な画面を示したものです.
Android版は「Google Play」で検索してください.
|
|
|
| インストール |
|
ダウンロードしたEXEファイルをダブルクリックすると,
ファイルは自動解凍されます.
解凍途中では,以下の事について確認が求められます.
特にこだわりが無ければ,「Ok」や「次に」を押し続けていればよいでしょう.
途中で確認を求められる主な事項は,下記の通りです.
以上の個々の画面を表示しながら ダウンロード・インストール手順を説明している サイトもあります.ただし, 古いバージョンで説明されているので, このページでの説明と若干違う部分もあるので注意してください. |
| gnuplotの起動 |
|
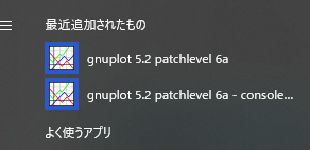
インストール後にスタートボタンを押すと,
「最近追加されたもの」として,
上部に「gnuplot」の名称のついた2種類のアイコンが表示されます.
「console-version」ではない方のアイコン,
つまり一番上に表示されるアイコンをクリックします.
誤って「console-version」を選択すると, 下図のようなDOSモードのgnuplotが立ち上がります.
|
| ■グラフ画面の諸設定 |
|
|
| 画面のフォント調整 | |||||||||||||||||||||||||||||||||||||||
|
gnuplotの初期画面では,
画面に表示されるフォントが小さすぎると感じるかもしれません.
そのフォントの大きさは自由に変更することができます.
カーソルを画面上において右クリックすると表示されるメニューから,
「Choose Font...」を選択します.
フォントの選択画面が表示されるので,
希望するフォントとサイズを指定します.
最新版をダウンロードするとデフォルトで日本語が使用可能になっているので,
サイズの箇所だけ指定すればよいでしょう.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 平面グラフの描画 | |||||||||||||||||||||||||||||||||||||||
gnuplotを利用すると,どのようなグラフが描画されるのかを
さっそく試してみましょう.
平面グラフの描画コマンドは「plot」です.
簡単な2次関数 \(\small y=x^2-2x\) のグラフ描画は,
次のように打ち込みます.
(注意) 分数係数を掛けるときは注意してください.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 座標軸の設定 | |||||||||||||||||||||||||||||||||||||||
gnuplot に対するいろいろな設定は「set」コマンドを利用します.
たとえば,座標軸を描画して,軸の名前(ラベル)を表示し,
軸の範囲を \(\small -2\le x\le 4, -2\le y\le 6\) に指定するには次のようにします.
■軸のラベル 軸に日本語を含めて入力しようとすると, 入力中の日本語がきちんと表示されないかもしれません. 入力が正しくできていればエラー表示はでません. 「replot」すれば,グラフ画面に日本語が表示されているはずです. 例えば,次のように入力してみます.
gnuplotが入力や出力で利用するフォルダーは, デフォルトでは「My Documents」です. そのフォルダーにファイルを置いているときは, ドラッグしないで「load 'test.plt'」とすることでもかまいません. gnuplotで利用するフォルダーを変更する方法は, 「履歴とグラフのファイル保存」の箇所を参照してください. 座標軸のラベルのフォントのタイプや大きさを指定することもできます. たとえば,\(\small x\) 軸であれば,「set xlabel font "FontType, FontSize"」 の形で指定し,「MS明朝」であれば 「set xlabel font "MS明朝, 14"」とします(図は略).
■矢印としての座標軸
目盛りやラベルを消すには,「unset xtics」「unset xlabel」などとします. その上で,座標軸を矢印で書き込みます. 矢印は,「set arrow A from 点1 to 点2」の書式です. 「A」には,その矢印に付すラベルです.適当な番号で指定します. 点1と点2は,たとえば (a,b) であれば,「a,b」で指定します. 矢印には,それぞれ異なる番号を付します. それにより,たとえば y軸方向の矢印に「2」を付したとき, それを消すには「unset arrow 2」とします. 矢印を引いただけでは目盛りは表示されません. 目盛りを表示させるには, たとえば x軸の場合は「set xtics axis」とします. デフォルトは「set xtics border」に設定されています.
★なお,グラフ画面を消去するコマンドは「clear」, 入力した各種の指定をすべて初期化するコマンドは「reset」です. 矢印の太さや矢尻の大きさなどを調整したいときは, 下記を参照してください. | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 座標軸の範囲と目盛り | |||||||||||||||||||||||||||||||||||||||
|
軸の範囲は「xrange」「yrange」で指定します.
簡略化して,それぞれ「xr」「yr」だけでもかまいません.
\(x\) 座標と \(y\) 座標はコロン(:)で区切ることに注意してください.
範囲指定を自動設定に戻すには「set autoscale」とします.
「replot」は,定義済みの関数のグラフを「再描画」させるコマンドです. 改めて関数の式を入力する必要はありません. 関数を描画後に範囲を指定するのではなく, 最初から範囲を与えて描画することもできます. その場合は,下記のように,関数の前で \(\small x\) 軸の範囲と \(\small y\) 軸の範囲を指定します.
座標軸の目盛りは自動的に付されますが, その間隔を自分で指定することもできます. たとえば,\(\small y\) 軸の目盛りを2刻みにするには 「set ytics 2」とします(図は省略). \(x\) 軸は「xtics」を利用します. 目盛りのフォントを指定するには, 「set tics font "FontType, FontSize"」のように指定します. たとえば,「set tics font "Times New Romman,14"」などとします(図は略). 目盛りの指定を削除するには「unset」を利用します. たとえば,\(\small y\) 軸の目盛りを削除するには「unset ytics」とします. \(y\) 軸の目盛りを削除して「replot」すると, 縦軸の目盛りが消えて単なる縦線になります(図は略). 「unset yrange」として「replot」すると, \(\small x\) 軸に指定した範囲のグラフが表示されるように \(\small y\) 軸の範囲が自動設定されます(図は略). なお,座標軸の範囲や目盛りの調整を試してみた場合は, この後の説明の都合上,下記の設定にしておいてください.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 色と線種の指定 | |||||||||||||||||||||||||||||||||||||||
|
グラフの色は関数が変わるごとに変わり,
8種類の色が順繰りに変化していきます.
どのような色が登録されているかは,「show linetype」により表示されます(図は略).
色に名前がついていないものはrgbコードで表示されます.
ただし,コードだけでは色のイメージが沸かないので,
私の感覚(イメージ)で名前をつけました.右列のイメージの箇所は,
一部を除いて正式な色の名前ではありません.
グラフの線種はデフォルトでは実線になりますが, 点線や破線で描画させることもできます. その指定は「plot f(x) dashtype N」として,Nの番号で指定します. Nの値により,次のような線種を指定することができます. 「dashtype」は「dt」と簡略指定することができます.
以下では,\(\small f(x)=x^2-2x\) として, 線種を変えながら\(\small y\) 軸方向に平行移動しています. 色はgnuplotが自動的に変えています. 指定には簡略化した記法を使っています.
個々の関数ごとに指定しながら「replot」するのが面倒なときは, 個別に指定しながら「,」で区切って次のように指定しても同じグラフが描画されます.
曲線の太さを変えるには, 「plot f(x) linewidth N」として, Nには具体的な整数を入れます.デフォルトのNの値は1です. このコマンドは,「plot f(x) lw N」と略記することもできます. また,曲線の色,線種,太さを続けて指定することもできます. 下記では,定義済みの関数 \(f(x)\) に対して, 赤色の点線で太さを5倍にしたものです. コマンドは略記しています. 関数ごとに同じような指定をしながら 「,」で区切って指定していくと, 複数の関数のグラフを一気に描画することができます.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 格子線(グリッド)の表示 | |||||||||||||||||||||||||||||||||||||||
グラフが分かりやすいように,格子線(グリッド)を表示させることもできます.
「set grid」により,グリッドが表示されます.
グリッドを非表示にするには,「unset grid」とします.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| グラフ画面のサイズ | |||||||||||||||||||||||||||||||||||||||
gnuplotのグラフ画面は,\(\small x\) 軸や \(\small y\) 軸の範囲を同じにした場合でも
横長の画面に表示されます.
外枠の縦横の長さを同じにするには「set size square」とします.
これによりグラフを描画する画面が正方形になりますが,
それぞれの範囲指定の仕方により目盛りの幅は異なります.
「set size ratio a」として,
\(\small a\) には縦\(\small /\)横の値を入れることでも画面枠のサイズを
調整することができます.
「set size x, y」とすると \(\small 横:縦=x:y \) になります.
下図は,
なお,正方形状にした画面を元に戻すには, 「set size nosquare」または「set size noratio」とします. 以後の説明は,デフォルトの画面幅で行います. | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 凡例の調整 | |||||||||||||||||||||||||||||||||||||||
グラフを描画すると,画面の右上に関数の式とグラフの色が表示されます.
その部分を「凡例」といいます.
この凡例の表示方法は,下記のように変更することができます.
下図は,凡例に関して次の指定をしたものです. タイトル部分ではべき乗記号が使用できるようです.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| メニューの利用 | |||||||||||||||||||||||||||||||||||||||
|
以上の設定は,メニューから行うこともできます.
軸に関する諸設定は「軸(A)」の箇所に,
再描画は「プロット(P)」の箇所に登録されています.
下図は「軸(A)」のメニューです.メニューを利用して指定しても,
gnuplotの画面には自分で入力したものと同じ内容が書き込まれます.
自己入力とメニュー利用のいずれが簡単かの判断は,
それぞれのPCの利用スタイルによると思うので一概には言えません.
メニュー利用の場合は,個々のコマンドを覚える必要はありません.
コマンドを忘れたときはメニューを利用するとよいでしょう.
| |||||||||||||||||||||||||||||||||||||||
| コメントの挿入 | |||||||||||||||||||||||||||||||||||||||
|
個々のコマンドの概要を把握できるように,コメントをつけることもできます.
「#」をつけると,それ以降の部分はコメント文として扱われます.
行頭につけると,その行全体がコメント行になります.
下記では行頭につけています.
コマンドの履歴を保存して後で再利用したいときは,
コメントをつけて保存しておくとよいでしょう.
ただし,コメント部分に日本語を入力することはできません.
履歴の保存方法は後述します.
|
| ■定数と関数の定義 |
|
|
| 定数の定義 |
|
gnuplotでは,定数として円周率 \(\small \pi\) は「pi」として定義されていますが,
ネイピア数 \(\small e\) は定義されていません.
その値を使用するには「exp(1)」として利用します.
あるいは,「e=exp(1)」として文字「e」に定義しておけば,
「exp(x)」は「e\(\small **\) x」として利用することができます.
係数が複雑な式のときに,
いちいちそれを打ち込むも大変です.
その式を定義する前に,
たとえば「a=sqrt(2/pi)」などと定義しておいて「a」を利用するととよいでしょう.
定義済みの定数は「print 定数」により確認することができます.
「show variables」とすると,gnuplotが認識している定数が表示されます.
定義した定数を削除するには「undefine 定数」とします.
個別に削除するのが面倒なときは「reset session」とします.
すべての設定が削除され,gnuplotの初期状態に戻ります.
上図では,e, aを定義して,「print」を利用して値を表示させています. また,「show variables」により,その時点で定義されているすべての定数を 表示しています.gnuplotの幾つかの内部定数も表示されますが,気にしないことです. pi, a, e が含まれていることが確認できます. その下では「undefine」を利用して a を削除し, 実際に削除されたことを「print」と「show variables」で確認しています. |
|
|
| 数値計算(複素計算) |
|
gnuplotを電卓代わりに利用することもできます.
計算式を直接打ち込むとコマンドとして理解しようとして
エラーが表示されるので,「print」を利用します.
★このことは、関数を定義するときも注意する必要があります。たとえば、 「plot 2/3*x」とすると、直線「y=0」が描画されます。「plot 2.0/3*x」または 「plot 2/3.0*x」とする必要があります。 複素数を扱うこともできます.\(\small a+bi\) は {a,b} で表します. 虚数単位は {0,1} なので,この値を I としておけば 複素数は「a+b*I」として利用することができます. |
|
|
| 関数の定義 |
|
関数 \(\small f(x)\) を定義するには,
単に,\(\small f(x)=(xの式)\) として定義するだけです.
2変数関数も同様に,\(\small f(x,y)=(x,yの式)\) とするだけです.
12個の引数まで利用できます.
定義した関数を削除するには「undefine GPFUN_関数名」とします.
たとえば,関数として func(x,y) を定義しているのであれば,
「undefine GPFUN_func」とします.
単純な式に留まらず,次の項目にある条件分岐や繰り返し処理などを
利用することで,かなり複雑な関数も定義することができます.
|
| 条件分岐と繰り返し処理 |
条件分岐をする関数を定義するには,
三項演算子が利用できます.
書式は「条件式 ? 処理1 : 処理2」の形で使用します.
条件式が真のときは処理1が実行され,偽のときは処理2が実行されます.
入れ子にして使用することもできます.たとえば,
\[\small f(x)=\begin{cases} -x-2 & (x<-2)\\
x+2 & (-2\leq x<-1)\\ -x & (-1\leq x< 0)\\
x & (0\leq x)\end{cases}\]
を定義するには次のようにします.
繰り返し処理を行うこともできます. 書式は「do for [変数 = 開始:終了:増加数] {処理1;処理2;処理3}」 のようにします.たとえば,単純に1から10までの和の計算は次のようになります. [i=1:10:3]のように指定すると3刻みの和となります. 「while」文も利用できます. 書式は「while (評価式) {処理1;処理2;処理3}」のようにします. 評価式が0ではない間,処理が続行されます.whileを使用する場合は, 「0ではない間で実行される」ような評価式で設定する必要があります. 「if」文は「if (条件式) {処理1;処理2} else {処理3;処理4}」 のような書式で利用することができます. たとえば,下記では,区間 \(\small [0,1]\) の乱数(rand(0))を発生させて, 0.5より小さいか大きいかを判断しています. do for [i=1:10] {a=rand(0); if (a<0.5) {print "small ",i,a} else {print "big ",i,a}} このように入力式が長くなるときは,下記のように改行しながら入力するとよいでしょう.
|
| ■2次元グラフの描画 |
|
|
| 関数の入力と定義 | |||||||||||||||||||||||||||||||||||||||
|
gnuplotでは,いろいろな関数を扱うことができます.
円周率 \(\small \pi\) は,「pi」により参照することができます.
入力するときの書式は,下記の通りです.
自分で関数を定義するときは, 「f(x)=・・・」の形で定義します. そのグラフは「plot f(x)」により描画されます. 下記では,\(\small f(x)=x^2-\pi x\) を定義してグラフを表示させています. 「plot」の後ろで \(\small x\)と\(\small y\) の範囲を最初に指定しています. 前の設定で座標軸の描画とグリッドの指定をしていれば, その指定を引き継いでグラフが描画されます.
適当な文字定数を使用することもできます. 下記のようにしても上図と同じグラフが描画されます. あるいは,「f(a,x)=x\(**\)2\(-\)a\(*\)x」と定義しておいて, 「plot f(pi,x)」のようにすることもできます.
「plot f(x), g(x)」などとすると, 複数の関数のグラフを描画することができます. あるいは,「plot f(x)」の後で「replot g(x)」としてもかまいません. グラフの線種や色等の指定の仕方は「グラフ画面の諸設定」を参照してください. | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 媒介変数表示によるグラフ | |||||||||||||||||||||||||||||||||||||||
gnuplotは,
\(\small x=f(t),\, y=g(t)\) のように \(\small t\) を媒介変数として
表された関数のグラフも描画することができます.
極座標で \(\small r=f(\theta)\) と表されている場合は,
\(\small x=f(t)\cos{t}, y=f(t)\sin{t}\) により\(t\)
を媒介変数として表すことができます.
媒介変数を利用できるようにするには,最初に
xrange, yrange により座標軸の範囲を指定することができますが, 新たに trange により媒介変数の範囲を指定することができます. \(\small x=f(t),\,y=g(t)\) の \(\small a\le t\le b\) の範囲のグラフを描画させるには, 「plot [a:b] f(t), g(t)」とするだけです. 事前に「set trange [a:b]」を実行していれば, 「plot f(t), g(t)」だけでかまいません. デフォルトでは,\(\small -5\le t\le 5\) に設定されています. サイクロイドは,次により描画されます. \(\small t\) の範囲は,trangeを使用しないで関数の組の前で直接指定しています.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 異なる座標系のグラフ | |||||||||||||||||||||||||||||||||||||||
|
前項でみたように,
「set parametric」として媒介変数を利用すると
極座標で表された関数のグラフも描画することができます.
直交座標で \(\small y=f(x)\) と表された関数も,
媒介変数を利用すると \(\small x=t, y=f(t)\) と表すことができます.
つまり,媒介変数のグラフモードにしておくと,
3種類のタイプのグラフを同じ画面に描画することができます.
例えば,単位円,心臓型曲線(カージオイド),そして正弦曲線 を同じ画面に描画するには次のようにします. 画面設定は前項のものを引き継ぎ,\(\small x\) 軸の範囲だけ変更します. 「set parametric」はすでに実行済みで, 媒介変数 \(\small t\) の範囲も前項ですでに定義済みです.
このように,一つの曲線をplotした後は,replotを利用して 次々にグラフを重ねがきすることができます.ただし,replotすべきところで plotを利用すると,前に描いたグラフは消えてしまうので注意してください. その場合は,最初からやり直すしかありません. | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 極座標によるグラフ | |||||||||||||||||||||||||||||||||||||||
極座標で表された関数のグラフは,前項により
媒介変数表示に変換して描画することができますが,
「set polar」によりグラフ画面の座標系自体を極座標に直すこともできます.
元に戻すには「unset polar」とします.
さっそく試してみましょう.
前項と同じ三葉線を描画させてみます.
なお,xrange, yrange の指定は \(r\) の値よりも優先されることに留意してください. たとえば,上記の状態で「plot 3\(*\)sin(3\(*\)t)」を実行すると, この画面に納まる部分だけが表示され,三葉線の全体像は表示されません(図は略). | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 点を線で繋ぐ | |||||||||||||||||||||||||||||||||||||||
関数のグラフではなく,指定された点を線分で繋いでいくことで
得られるグラフもあります.
複数の点を線分で繋ぐには,「plot "-" with lines」
とします.そうすると,点の座標を入力することが求められるので,
コンマ区切り(,)ではなく,半角の空白区切りで座標を入力します.
空白行を入力すると,次に入力する点が新たな始点になります.
入力を終えるときは「e」を入力します.
下記では,単純な三角形を,赤の点線で,
ちょっと太めで描画しています.
lw は「line width」,ltは「line type」の略記です.
「with lines」は,「w l」で済ませることもできます.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| 離散データのグラフ | |||||||||||||||||||||||||||||||||||||||
|
実験等で得られる離散的な数値データをグラフ化することもできます.
数値データはデフォルトでは空白で区切られますが,
「set datafile separator ","」とすることでコンマ区切りの
データも読み込むことができます.
試みに, ランキングサイトをもとに, 平成27年の国勢調査による県庁所在地47都市の人口を図示してみましょう. 最初に,このサイトのデータをもとに, コンマ区切りの データ (jinkou.dat) を作成します.各行は「順位, 人口,人口密度」で, 人口の単位は「千人」,人口密度は1平方キロメートルあたりの人数(整数)です. デフォルトでは, データファイルは「My Documents」にあることが想定されているので, 必要に応じてデータファイルを置くフォルダーを変更しておきます. トップメニューの「ファイル(F)」から 「ディレクトリーの移動」を利用してください. データが用意できたら,下記によりグラフが描画されます. 空白区切りのデータでは,最初のコマンドは不要です.
| |||||||||||||||||||||||||||||||||||||||
|
1. プロット記号
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
2. 線で繋いで描画する
記号を付して線で繋ぎたいときは,「with linespoint」とします.
略して「w lp」でもかまいません.例えば,白丸「○」を付して
線で繋ぐには,
「plot "ファイル名" with linespoint pointtype 6」とします.
簡略化して
「plot "ファイル名" w lp pt 6」とすることもできます(図は略).
| |||||||||||||||||||||||||||||||||||||||
|
3. 棒グラフで描画する
| |||||||||||||||||||||||||||||||||||||||
|
4. 複数の列データを描画する 以下では,スマホでの表示の関係で, 「 \」を入れてできるだけ改行しながら入力しています. 実際には,1行で続けて入力してください.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
5. 座標軸を書き入れる
| |||||||||||||||||||||||||||||||||||||||
|
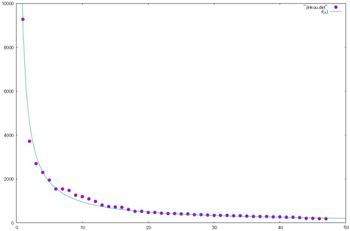
6. 別な曲線を書き入れる
県庁所在地の人口はいろいろなはずですが,順番に並べると \(\small 10000/x\) という分布に従っていることが分かります. これは \(\small (人口)\times(順位)=10000\) という関係にあることを 示しています.このように,順位との積が一定値であるような関係は, 「ジップ(Zipf)の法則」と呼ばれています. また,一般に \(\small C/x^a\) のようなベキ関数で表される分布は「ベキ分布」 と呼ばれ,世の中のマクロからミクロの世界まで, さらには人間のかかわるいろいろな場面で頻繁に現れてきます. 「ベキ分布:リンク集」も参照してください。 | |||||||||||||||||||||||||||||||||||||||
|
7. 凡例を変更する | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
8. 座標軸を対数軸にする 周知のように,常用対数は,いろいろな値(\(\small M\))を \(\small M=10^a\) の形で表して,指数部分の \(\small a\) の値で 考えようとするものです.天文学的な \(\small 10^{20}\) のような大きな値や, ミクロの世界の \(\small 10^{-10}\) のような小さな値も, 対数をとると \(\small -10\sim 20\) の取り扱いやすい値に変換することができます. 座標軸を対数軸にするには「set log」を用います. 解除するには「unset log」です.
対数の値は \(\small 0\) では定義されないので, それを含まない区間を指定しました. \(\small 100=10^2, 1000=10^3, 10000=10^4\) なので, 対数軸の実際の目盛りは \(\small 2\sim 4\) の範囲となります. \(\small y\) 軸の目盛りを \(\small 10^a\) の形で表示させることもできます. 「set format y "10^{%L}"」とします. 元に戻すには「unset format」とします. 目盛りに関する詳細はこちらも参照してください.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
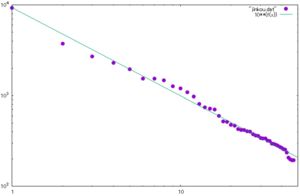
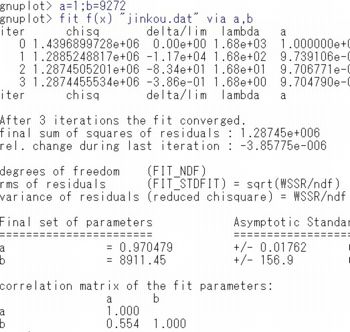
9. 曲線回帰をする 「8」の人口のデータを両対数グラフで描画した場合は, 右下がりの直線で回帰できそうです. 通常データで直線回帰する場合は, 最初に「$\small f(x)=a+b*x$」として関数を定義した上で, 「fit f(x) "データファイル名" via a,b」とすれば, 「plot f(x)」(データと重ねるには「replot f(x)」)とするだけで 回帰直線が描画されます. ただし,ここでは両対数グラフで描画されたデータに対して 直線回帰しようとしています. データファイルに対数の値も追加してそのデータを利用してもよいですが, gnuplotでは使用する列データを「using」を利用して指定できます. その列データを対数に変換して利用することができます. 2列目を常用対数に変換するには,「using 1:(log10($2))」とします. 改めてまとめると,両対数グラフが直線状になるのは,
元のデータが $\small y=C/x^{\alpha}$ の形のときです.
常用対数をとると $\small \log10(y)=\log10(C)-\alpha\log10(x)$ となるので,
回帰式としては「$\small f(x)=a+b*\log10(x)$」を設定します.
得られた回帰直線は,「replot $\small 10**(f(x))$」とすることで
描画されます.
なお,gnuplotでは,常用対数は $\small \log10$,
自然対数は $\small \log$ です.
また,$\small 10^{\log10(x)}=x$です.
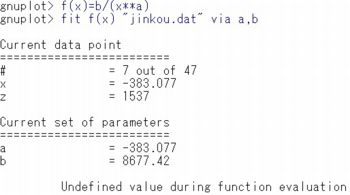
次に,両対数グラフにしないで,元データに対して回帰曲線を求めてみましょう. 「$\small f(x)=b/x^a$」として「fit」を実行すると, 次のようになります.
| |||||||||||||||||||||||||||||||||||||||
|
両対数グラフの場合は,$\small f(x)=a+b\log10(x)$ としたので,
\begin{align*}
\small f(x)&\small =\log10(10^a)+\log10(x^b)\\
&\small =\log10(10^a x^b)\\
&\small =\log10\dfrac{10^a}{x^{-b}}
\end{align*}
としたことになります.この場合の回帰結果は
$\small a=3.96968, b=-0.971938$ であるので,
$\small 10^a=9325.67$ となります.
一方,元データに対して $\small f(x)=b/x^a$ とした場合は $\small a=0.970479, b=8911.45$ となります. $\small b$ の値がかなり違うように見えますが, 9325と8911の差は414であり,僅かに4%程度の違いがあるだけであり, グラフ表示するとほとんど重なって表示されます(図は略). | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
10. データの統計情報を得る
デフォルトでは,データファイルの1列目と2列目について, それぞれの平均や分散等の値が出力されます. 「Skewness」は「歪度」,「Kurtosis」は「尖度」, 「Sample StdDev」は「不偏分散」, 「Quartile」は「四分位数」で上から順に3つの値が示されています. 周知のように,第2四分位数は要するにメディアンです. 特に指示をしなくても,直線回帰までしてくれています. 3列以上あるときは,出力する列を「using」で指定することができます. | |||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
| ヒストグラムの描画 | |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
データファイル 離散データでは,ファイルに書き込まれた順にグラフが描画されていきます. 値が激しく変動するデータファイルから, 度数分布表を作成してヒストグラムを描画させることもできます. ここでは,次のサンプルファイル(random_smp.csv)を利用します. Maximaの確率分布に関するコマンドを利用して, 二項分布,一様分布,正規分布,ベキ分布(パレート分布)にしたがう乱数を, それぞれ1000個ずつ発生させたものです. gnuplotのデータは列データである必要があるので,このファイルは要するに \(\small (1000, 5)\)型の行列データです.
| |||||||||||||||||||||||||||||||||||||||
|
連続データの場合 gnuplotにより,値の大小がばらばらのデータから ヒストグラムを作成して描画する方法を解説しているサイトは, あまりありません.以下の解説は, 下記を参照して作成したものです. では,用意したデータファイルの第4列「正規分布N(50,10)」を利用して, さっそくヒストグラムを描画してみましょう. 最初に,サンプルファイルをダウンロードして, 利用するフォルダーに置いておきます. 現在のフォルダーの確認やフォルダーの変更は, 「ファイル(F)」の箇所で行うことができます.フォルダー間のファイルの移動は, エクスプローラーなどを利用してください. 描画の手順は,下記の通りです.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
度数分布表の作成 ヒストグラムを描画することはできても, 各階級の度数まではグラフに表示されません. gnuplotには,階級ごとの度数分布表を出力させる機能があります.
| |||||||||||||||||||||||||||||||||||||||
|
離散データの場合 離散データの場合も同様です.以下は, 使用しているデータファイルの2列目にある二項分布Bin(10,1/6)を 利用したものです. まず,1行目で階級幅を1に変更します. 2行目では,階級値の計算式を変更して整数値にしています. その上で,3行目で柱(boxes)と折れ線(lines)による描画をしています. 以下の「$」は,実際には半角で入力してください.
| |||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||
|
不均一な階級幅 「binwidth」で階級幅を指定すると, 基本的には指定した階級幅で区分されます. ただし,値が大きく飛んでいて度数の存在しない階級が存在するようなときは, 幾つかの階級が自動的にまとめられて描画されるようです. そのような値が生じる場合として「ベキ分布(パレート分布)」があります. 使用しているデータファイルの5列目は,確率密度関数が \(\small 1/x^2~(x\geq 1)\) で表されるベキ分布にしたがう乱数です.簡単な計算から分かるように, この確率分布は平均も分散も存在しません(参照). そのような確率分布にしたがう乱数を発生させると, 値の変動はすさまじいものになります.
それに対して,ベキ分布にしたがう乱数は,値の飛び幅が半端ではありません. 下図は,縦軸を対数軸に取って描画したものです.大部分は10以内になっていますが, 100を超える場合がかなりあり,1000に近い値になることもあります. 何度か乱数を発生させると,1000を超える値が発生する場合もあります.
| |||||||||||||||||||||||||||||||||||||||