�u�ׂ����z�v�����߂āC���̐��E�����낤�I
(��) MathJax���g�p���Ă���̂ŁA �X�}�z�ł͕\���Ɏ��Ԃ������邱�Ƃ�����܂��B
���o�C�����p(Android)�ł̃��j���[�I���́A SiteMap�𗘗p���邩�A �u�������v����u�V�����^�u���J���v��I�����Ă��������B
| �� �u�ׂ����z�v�F�����N�W �@[Map] |
|
|
|
|
|
[��ē�] �m�����v�̎��Ƃ́u���K���z�v�����\�ł��邩�̂悤��
���ƍ\���ɂȂ��Ă��܂����C
���̒��͕��ς╪�U�����݂���Ƃ͌���Ȃ��u�ׂ����z(�p���[�g���z)�v�� �x�z����Ă���悤�ł��D �����ł́C�u�ׂ����z�v��u�ׂ��摥�v�ɂ��ĉ�����Ă���Web�T�C�g�� �_�������܂Ƃ߂܂����D �@�Ȃ��CMaxima�𗘗p��������� �u�������v���C �uR�v�𗘗p��������́u�������v���Q�Ƃ��ĉ������D |
| �͂��߂�(�T��) | ||||||||||||||||||||||||||||
|
�����ł́A�u�ׂ����z�v���V���̂悤�ȃ}�N������_�o��H�̂悤�ȃ~�N���̐��E�܂ŁA
����ɂ͊����ϓ���푈�Ɋւ��邱�Ƃ܂ŁA
���̒��̎���Ƃ���Ɍ���Ă��邱�Ƃ��Љ�܂��B
���̌�ŁA�ȒP�ȊT�v��������܂��B
| ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�Ƃ́H �m�����z�ɂ��Ă�����x�w�l�ł����Ă��C �u�ׂ����z�v�ɂ͓���݂̂Ȃ��ꍇ�������Ǝv����̂ŁC �ŏ��ɋ�̗���Љ�܂��D
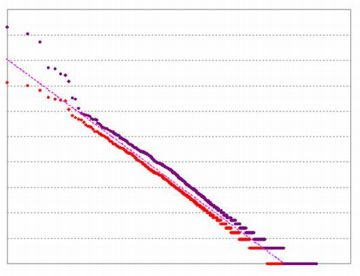
�������ݒn�̐l�� (��) ���̃f�[�^����A���� \(\small y=C/x^{a}\) �ɂ��Ă͂߂�� \(\small C=8911, a=0.97\) �������܂����C ���̐��l���g���Ă��O���t�͏�}�ƂقƂ�Ǐd�Ȃ�܂��D �{���� \(\small y=9272/x\) �Ŏ����ׂ��ł����C�ȒP�̂��ߏ㎮�Œ��܂����D����́C \(\small (�l��)\approx 10000/(����)\) �Ƃ������Ƃ������Ă���C ������� \(\small (�l��)\times (����)\approx 10000\) �C �܂�l���Ə��ʂ̐ς��قڈ��ł���Ƃ������Ƃł��D ���ہC���̂悤�ɂȂ��Ă���u10,000�v�̑O��̒l�ɂȂ��Ă��邱�Ƃ� ������܂��D����́C���̏��ʂŌ��Ă����l�ł��D
��p�ΐ�
�g�߂ɂ���ΐ� | ||||||||||||||||||||||||||||
|
���ΐ��O���t �ȏ�̏����̂��ƂŁC�������ݒn�̐l���̃O���t�� �ΐ��𗘗p���ĕ`�悵�Ă݂܂��傤�D 5�ʂ܂ł̓s�s�̐l���̏�p�ΐ��̒l�́C���̂悤�ɂȂ�܂��D ��p�ΐ��̋�̓I�Ȓl�́C���Ƃ��� �ukeisan�v �𗘗p����Ƌ��߂��܂��D
�ׂ����z�̓���
�W�b�v(Zipf)�̖@�� | ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�̋�̗�
�y��1�z2�̕ϗ� \(\small x, y\) �̊Ԃ� \(\small y=Cx^{\gamma}\) �̂悤��
�ׂ���̊W������Ƃ��A2�̕ϗʂ̊Ԃɂ́u�ׂ��摥�v�����藧�ƌ����܂��B
�u�ׂ����z�v�� \(\small y=C/x^{a}=Cx^{-a}\) �ƕ\����̂�
�ׂ��摥�����Ă��܂��B
�ȉ��ɏЉ��啔���̗�́u�ׂ����z�v�Ɋւ�����e�ł����A
����u�ׂ����z�v�ł͂Ȃ����u�ׂ��摥�v�����Ⴊ�܂܂�Ă��܂��B
�܂��A�u�ׂ����z�v���u�ׂ��摥�v�ƌĂ�ł���ꍇ������܂��B
(1) �ΐ��Ɩؐ��̊Ԃɂ��鏬�f����
(2)
�n�k�̋K��(�}�O�j�`���[�h)�ƕp�x
(3)�X�e�����X��̐��H�̌�
(4)���z�[�Ŋz�Ə���
(5)�~�h���בփ��[�g�̕ϓ�
(6)�푈�̐펀�҂Ɛ푈�̐�
(7)�����L�[���[�h�ʂ̃A�N�Z�X��
(8)�זE����Ӄl�b�g���[�N
(9)�^���p�N�����ݍ�p�l�b�g���[�N | ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�̒�` ���̊m�����z�̖��x���́A���m�ɂ� \(\small a,b>0, C=ab^a\) �Ƃ���Ƃ��A ���̊��Œ�`����܂��B \[\small f(x)=\frac{C}{x^{a+1}}\quad (x\geq b)\] �v����ɁC�x�����z��q�X�g�O�������ׂ���Ō������Ă����悤�ȕ��z�ł��B �����҂̖��O�Łu�p���[�g���z�v�ƌĂ�邱�Ƃ�����܂��B �����āA2�ϗʂ����̂悤�Ȃׂ���̊W�ɂ���Ƃ��́u�ׂ��摥�v �����藧���Ă���Ƃ����܂��B ���ӂ̏�p�ΐ������� \[\small \log{f(x)}=\log{C}-(a+1)\log{x}\] �ƂȂ�̂ŁA\(\small Y=\log{f(x)}, X=\log{x}\) �Ƃ����� \[\small Y=\log{C}-(a+1)X\] �ƂȂ�A�w���������X���ɂ��E������̒����ɂȂ�܂��B �܂�A���ΐ��O���t ( [1] [2] ) �������ɂȂ�悤�ȕ��z���ׂ����z�ł��B ����ɁA�ׂ����z�̗ݐϕ��z�����l����ƁA �܂� \(\small P(X\leq x)=F(x)\) �Ƃ����� \[\small F(x)=\int_{b}^{x}f(t)\,dt=1-\frac{b^a}{x^a}\] �ƂȂ�̂ŁA\(\small P(X\geq x)=1-P(X\leq x)\) �ł��邱�Ƃ���A \(\small X\geq x\) �ƂȂ�m���� \[\small P(X\geq x)=\frac{b^a}{x^a}\] �ƂȂ�ׂ�����ŕ\����܂��B���̊��́u����ݐϕ��z���v�ƌĂ�܂��B ���̊��̗��ΐ��O���t���E������̒����ɂȂ�܂��B �ŏ��ɏЉ����ł́A(6)(7)������ݐϕ��z���ł��B �ׂ����z�̑傫�ȓ����Ƃ��āu���ȑ������v������܂��B \(\small x\) �� \(\small c~(c\gt 0)\) �{����ƁA \[\small f(cx)=\frac1{c^{a+1}}f(x)\propto f(x)\] �ƂȂ�A���Ƃ̊��Ɣ�Ⴕ�܂��B ������ \(\small c\) �{����ƁA �c���� \(\small 1/c^{a+1}\) �{�ɂȂ�܂��B �O���t�ł����ƁA�c���ł��� \(\small y\) ���� \(\small c^{a+1}\) �{����� ���Ƃ̃O���t�Əd�Ȃ��Ă��܂����ƂɂȂ�܂��B ���̂悤�Ȑ����������� \(\small Cx^{\gamma}\) �̌`�ׂ̂����������݂��܂���[�Q��]�B | ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�̃O���t ���}�́A�ȒP�̂��� \(\small b=1\) �Ƃ��� \(\small f(x)=a/x^{a+1}~(x\geq 1)\) �̃O���t��`�悵�����̂ł��B �Q�l�܂łɁA�W�����K���z N(0,1) ���E����1�������s�ړ������O���t N(1,1) ���`�悵�Ă��܂��B�����̎d�����A�w�����ŕ\����鐳�K���z�����x�����Ƃ�������܂��B �܂�A�w�����̂悤�ɋ}���Ɍ������邱�ƂȂ��A �u�_���_���Ɓv�ǂ��܂ł������������Ă����̂��ׂ����z�ł��B �܂�A���K���z�ƈႢ�A�傫�Ȓl�̔����m�����ł��Ȃ��̂ł��B ���̂��Ƃ́A�ׂ����z�ɏ]��������������ƁA ���܂Ƃ�ł��Ȃ��傫�Ȓl���������邱�ƂɌq����܂��B ���̃O���t�́A ���������\�t�g�uMaxima�v�ŗ��p����Ă��� �O���t�`��\�t�g�ugnuplot�v�ɂ����̂ł��B ��\(\small P(X\geq x)=b^a/x^a\) �̏ꍇ���A �ׂ��w����1����邾���Ȃ̂ŏ�L��2�̃O���t�Ɠ��l�̃O���t�ɂȂ�܂��B �ŏ��ɋ�̗�Ƃ��ă��X�g�A�b�v�����l�X�ȏ�ʂł́A �m�����x����q�X�g�O�����𗼑ΐ��O���t�ŕ\���Ă���ꍇ�ƁA \(\small P(X\geq x)\) (����ݐϕ��z���Ƃ����܂�)�̃O���t�� �\���Ă���ꍇ�Ƃ����݂��Ă���̂ŗ��ӂ��ĉ������B | ||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�ɂ������������̕W�{���ς̕��z ����ϗʂ��ׂ����z�ɏ]���Ă����Ƃ���ƁA ��̓I�ɂ͂ǂ̂悤�ȕ��z�ɂȂ�̂��� �ׂ����z�ɏ]�������𗘗p���ăV�~�����[�g���Ă݂܂��傤�B �ȒP�̂��߁A\(\small a=1, b=1\) �̏ꍇ���l���āA �m�����x���� \[\small f(x)=\frac1{x^{2}}\quad (x\geq 1)\] �̏ꍇ���l���Ă݂܂��B ���̏ꍇ�́A���ς����U�����݂��܂���B ���Ƃ��C���ς� \[\small \int_{1}^{\infty}xf(x)\,dx =\int_{1}^{\infty}\frac1{x}\,dx =\infty\] �ƂȂ薳����ɂȂ�܂��B ���ς����݂��Ȃ��̂ŕ��U�����݂��܂���B
���āA
���������\�t�g�uMaxima�v�𗘗p����ƁA
���낢��Ȋm�����z�ɂ������������������邱�Ƃ��ł��܂��B
���̋@�\�𗘗p���āA�ׂ����z�ɏ]��������������10�̕W�{���ς����߂Ă݂܂��B
���}�́A10�̕W�{���ς�1���߂ăO���t�\���������̂ł��B
�����͉���ڂɋ��߂��l�ł��邩���A
�c���͂��̂Ƃ��̕W�{���ς̒l�ł��B
�W�{���ς����߂邽�тɁA10���ς̒l���傫���ϓ����Ă���̂�������܂��B
�W�{���ς�1000����ꍇ�����x���o�Ă��܂��B
������A�m�����z�Ƃ��Ă̕��ς����U�����݂��Ȃ��̂ł��B
��̓I�ɂǂ̂悤�Ȓl�ɂȂ��Ă��邩���݂�ƁA
���Ƃ��ΕW�{���ς� \(\small 1253.14\) �̂Ƃ��̌X�̒l��
\[\small 1, 2, 12503, 2, 1, 3, 1, 10, 1, 2\]
�Ƃ����l�ł����B���������݂̂������Ă��܂��B
�啔���͏����Ȑ��̒��ɁA5���̐�
\(\small 12503\) ��1�܂܂�Ă������߂�
�W�{���ς�1000�������Ƃ�������܂��B
���̂悤�ɁA�ׂ����z�ł͒l���_���_���ƌ������Ă����̂ŁA
�傫�Ȓl�̔����m���𐳋K���z�̂悤�ɖ������邱�Ƃ��ł��܂���B
���s�������Ă����ƁA���܂Ƃ�ł��Ȃ��傫�Ȓl���������邱�Ƃ�����̂ł��B
�Ȃ��A���̂Ƃ��̕W������ \(\small 3750\) �ł��B
���}�́A���̕W�{���ς̒l�ׂ̗ǂ����̍��̐�Βl�����߂����̂ł��B�܂�A \(\small k\) ��ڂɋ��߂�10�̕��ς� \(\small M(k)\) �Ƃ���ƁA \(\small |M(k+1)-M(k)|\) �̒l�̕ω��ł��B �l���傫������̂ŁA�c���͑ΐ����ɂ��܂����B �������U�����Ă���̂�������܂��B �Ȃ��A��i�̃O���t�Ƃ͈قȂ闐���ɂ����̂ł��B �������Ȃ���A ���ׂ̗ǂ����̍��̐�Βl�̒l����0.2���݂̓x�����z�����߂āA ���̃q�X�g�O������܂���O���t�ŕ`�悷��Ƃׂ����z�̌`����Ă��܂��B ���i�́A���ΐ��O���t�ɂ������̂ł��B�r������͒�����ɂȂ�A �ϓ��̐�Βl��������x�ȏ�傫�������ׂ͂����z�ɏ]���Ă��邱�Ƃ�������܂��B �܂�A���`���N�`���ɕϓ����Ă���悤�Ɍ����Ă��A ���̕ϓ��ׂ͂����z�Ƃ������̊m�����z�ɏ]���ĕϓ����Ă���Ƃ��� ���ƂɂȂ�܂��B | ||||||||||||||||||||||||||||
|
���u�ׂ����z�v�Ɋւ��鐔�w�I�ȉ�� �����ł́A�t���[�̐��������\�t�g�uMaxima�v��p�����V�~�����[�V�����������Ȃ���A �ׂ����z�́u���ςƕ��U�v�u���ȑ������v�u\(\small 80:20\) �̖@���v �u�W�b�v�̖@���v�u���z�̑������v�u���ς̕��z�v�Ȃǂɂ��ďڂ��� �������Ă��܂��B���v�����\�t�g�uR�v�𗘗p��������� �u�������v���Q�Ƃ��Ă��������B ���L�́C��v�ȓ��������܂Ƃ߂Ĕ��\�������̂ł��D
| ||||||||||||||||||||||||||||
|
|
| �u�ׂ����z�v�̉�� |
| �����ł́C�ׂ����z(�p���[�g���z)�ɂ��āA ��ʌ����ɉ�����Ă���T�C�g���Ƃ�܂Ƃ߂܂����D |
|
Wikipedia:�p���[�g���z Wikipedia�̋L���ł��D�ݐϕ��z���C�c�x�C��x�C���[�����g����ȂǁC ���̕��z�Ɋւ��铝�v�I�Ȓl���܂Ƃ߂Čf�ڂ���Ă��܂��D |
|
�ׂ��摥 Hatena Keyword�̋L���ł��D�ׂ��摥�ɂ��āA ���]�ځA�l�b�g���[�N�A�X�P�[���t���[�Ȃǂɂ��ĉ������Ă��܂��B |
|
�ׂ����z�Ɛ��K���z �ׂ����z�̎d�g�݂ɂ��āC���K���z�ƑΔ䂳���Ȃ��番����₷���������Ă��܂��D |
|
�ׂ����z(�ׂ��摥) ���K���z�ƑΔ䂳���Ȃ���C �ׂ����z�������낢��ȓ����ɂ��Ă܂Ƃ߂��Ă��܂��D |
|
�Ȃ��݂̐��K���z�ɗ��Ƃ����A
�Ƃ��ɂ́u�u���b�N�E�X�����v�̊T�O�ő����邱�Ƃ��K�v �ߋ��ɗ�̂Ȃ����ۂ��Љ�ɑ傫�ȏՌ���^���錻�ۂ́A �u�u���b�N�E�X�����v�ƌĂ�܂��B �u�ׂ����z�v�������Ă���u�u���b�N�E�X�����v�̍l�����ɂ��� �Љ��Ă��܂��B |
|
|
|
�����L���O�f�[�^�̖@���� ���낢��ȃ����L���O�f�[�^���ׂ��摥�ɏ]���Ă��邱�� (���ꂪ�u�W�b�v�̖@���v�ł�)���Љ����ŁC ���̗��ΐ��O���t�������ɂȂ邱�ƁC �����Ē����̌X���̈Ӗ��ɂ��ĉ������Ă��܂��D |
|
�p���[�g�̖@���ƃ����O�e�[���̖@�� �ׂ����z�����ƂɌ��������ꂽ�u�p���[�g�̖@���v�ƁA ���̕��z�̓����ł���u�����O�e�[���v�ɂ��ĉ������Ă��܂��D |
|
�^���̊�{�����`��B�x�̖@���w�ׂ��摥�x�` �u�ׂ��摥�v���ǂ̂悤�Ȃ��̂�������������ƂŁA ���낢��Ȋw�K�̏�B�x���ׂ��摥�ɏ]�����Ƃ��q�ׂ��Ă��܂��B |
|
�ׂ��摥�̉\�� �l�u���O�ł��B �l�b�g���[�N�̎������z���ׂ����z�ƂȂ�BA���f�����l�Ă��� �A���o�[�g�E���Y���E�o���o�V�ɂ�钘���u�o�[�X�g�v�̓��e���A �������ďЉ��Ă��܂��B |
|
|
| �u�ׂ����z�v�̋�̗� |
| �����ł́A�u�ׂ����z�v��u�ׂ��摥�v�̎���ɂ��āA ��ʌ����ɂ܂Ƃ߂Ă���Web�T�C�g�����܂Ƃ߂܂����B |
|
���H�E���H�ɂ݂�ׂ��摥 ����j���Ƃ��A���̔j�Ђ̑傫���ƌ��Ƃ̊W�ׂ͂����z�� �����������Ƃ��m���Ă��܂��B ���H�̑傫���ƓH���̊W�ɁA ���̂��Ƃ����藧���ǂ����������I�ɒ��ׂ��Ă��܂��B |
|
��w�Ԋi���ׂ͂��摥�ɂ������� ������w�̉^�c��t���⋣���I�����̔z�����ׂ��摥�ɂ��������Ă��邱�Ƃ� �Љ��Ă��܂��B |
|
�����L�[���[�h���ׂ����z�������I Web�T�C�g�̌����G���W���o�R�̗����L�[���[�h�ʂ̃A�N�Z�X���� �ׂ����z�ɏ]���Ă��邱�Ƃ�������Ă��܂��B |
|
�u�͂Ăȃu�b�N�}�[�N�v�ׂ͂��摥�ɂ��������Ă���̂����ׂĂ݂� �u�͂Ăȃu�b�N�}�[�N�v�ƋL���̐��̊W�ɂ��āA �ׂ��摥�ɏ]���Ă��邩�ǂ��������ׂ��Ă��܂��B |
|
AKB48��2014�N�I�����I���ƃW�b�v�̖@�� AKB48��2014�N���I�����A���Ȃ肫�ꂢ�ȃW�b�v�̖@���ɓ��Ă͂܂��Ă���悤�ł��B |
|
TeX����ł�Zipf�̖@���͐��藧���H �W�b�v�̖@���͕p�x�Ə��ʂ̊W���ׂ��摥�ɏ]���Ă���Ƃ������̂ł����A ���̂��Ƃ�TeX�̃R�}���h�ɂ��Đ��藧���ǂ��������ׂ��Ă��܂��B |
|
�V���̋O���Ɋւ���"�ׂ��摥"�ɂ��� ���z�̘f���̋O�������a�Ƙf���ԍ��A ���邢�͖ؐ���y���̉q���̋O�������a�Ɖq���ԍ��̊Ԃ� �u�ׂ��摥�v�����藧���Ă��邱�Ƃ�����Ă��܂��B (�����́u�ׂ����z�v�ł͂���܂���B) |
|
|
| �u�ׂ����z�v�Ǝ��R���� |
| �����ł́A���R���ۂ̒��Ɍ�����u�ׂ����z�v��������Ă���A ������x���I�ȉ����_�������܂Ƃ߂܂����B |
|
���O���X�Ίp���C���x���g���f����Ώ̂Ƃ���L��T�[�x�C�ϑ� �ΐ��Ɩؐ��̊Ԃ̗̈�ɂ��鏬�f���тɂ��āA ���f���̒��a�Ɨݐό����ׂ����z�ɂ��������Ă��邱�Ƃ�������Ă��܂��B |
|
�N���[�^�T�C�Y�p�x���z���炳���錎�f���\�ʂ̒n���i�� ���{�f���Ȋw��Ɍf�ڂ��ꂽ���̂ł�(2015�N)�B ���̃N���[�^�[�̒��a(D)�ƁA���̃T�C�Y�̃N���[�^�[�̐����x�̗ݐϕp�x���z N(\(\small \geq D\))�̊W���ׂ����z�ɂ��������Ă��邱�Ƃ�������Ă��܂��B �N���[�^�[�͎��ԂƂƂ��ɑ������邪�o�N�ω��ŏ��ł�����̂�����A ���郌�x���ɒB����ƕ��t��ԂɂȂ��ăN���[�^�[�̐����x���������Ȃ��Ȃ�悤�ł��B �n���̔N��ƃN���[�^�[�̃T�C�Y�A�Ȃ�тɂׂ��w���̊W�ɂ��ďq�ׂ��Ă��܂��B |
|
���z�^���̃X�[�p�[�t���A �����V���䉪�R�V�̕����ϑ����̌����҂��A�P�v���[�]�����̊ϑ��f�[�^�����ƂɁA ���z�^�t���A�̃G�l���M�[�Ɣ����p�x�𗼑ΐ��O���t�ŕ`�悷��� �����ɂȂ邱�Ƃ��A�X���C�h�ʼn������Ă��܂�(2017�N)�B |
|
�n�k���ۂ̐V�������� �u�n�k�v�Ɍf�ڂ��ꂽ���̂ł�(1991�N)�B �J�I�X��t���N�^���Ȃ����G�����Ɋւ��Ė��炩�ɂȂ��Ă������Ƃ����ƂɁA �n�k���u�S�̂̕��G���������̕��G���v�ł���t���N�^���Ȍ��ۂƂ��āA ���ȑg�D���ՊE���ۂƂ݂錩���ɂ��ĉ������Ă��܂��B ����1990�N�����ɔ������Ă��邱�ƑS�ʂɓn����������Ă���̂ŁA ���]�ځE�ՊE���ۂ��܂ޕ��G�n�̑S�̑���c������Ƃ��L�v�Ǝv���܂��B |
|
�ΎR�Ɋւ���T�C�Y�̘b �_�ˑ�̃T�C�G���X�Z�~�i�[�ł̍u���L�^�ł�(2007�N)�B �ΎR�ł̕��o���╬�̋K�͂Ȃǂ��ׂ����z�ɏ]�����Ƃ��������Ă��܂��B |
|
�ΎR�����w��(VEI)���猩�����̋K���� �u�ΎR�v�Ɍf�ڂ��ꂽ���̂ł�(2015�N)�B �n�k�̋K�͂ƕp�x�ׂ͂��摥�ɏ]���Ă��邱�Ƃ� �O�[�e���x���O�E���q�^�[���Ƃ��Ēm���Ă��܂����A �ΎR�̕��̋K�͂ƕp�x�ɂ����Ă����l�ׂ̂��摥��������悤�ł��B �X�̉ΎR�݂̂Ȃ炸�A�ΎR�n���ΎR�ʂɂ����Ă����l�ׂ̂��摥�� �����邱�Ƃ�������Ă��܂��B |
|
�J�ƍ��R�����[�J�̍~����ɐ��ޖ@���� �u�V�C�v�́u�C�ےk�b���v�Ɍf�ڂ��ꂽ�L���ł�(2018�N)�B �A���_�X�̃f�[�^�����Ƃɓ����s�̉J�̍~����ׂ�ƁA �~���ʂƍ~���ׂ͂����z�ɏ]���Ă��邱�Ƃ�������Ă��܂��B |
|
�Ռ��j��̓��v�� ���k��w�̐搶�̃T�C�g�ł��B �j�ۂɂׂ����z������邱�Ƃɂ��ĉ������Ă��܂��B ���郂�f���ɂ��V�~�����[�V�����ŁA �ׂ��w�� \(\small 2/3\) ������ꂽ���Ƃ��q�ׂ��Ă��܂��B |
|
|
| �u�ׂ����z�v�Ɛ������� |
| �����ł́A�����E�̌��ۂ̒��Ɍ�����u�ׂ����z�v��������Ă��� ���I�Ș_�������܂Ƃ߂܂����B |
|
���̐����n���w��Zipf�̖@�� ���ɏZ�ގ�̐�(S)�́A���̖ʐ�(A)�ׂ̂���ɔ�Ⴗ��W \(\small S\propto A^z\)�ɂ���悤�ł��B �܂��A�ő̂̐�(x)�ƌ̐�x�ȏ�̎퐔�̕p�xP(\(\small \gt x\))�� �W�ׂ͂���̊W�ɂ���P(\(\small \gt x)\propto x^{-\alpha}\) �� ���藧���Ă���悤�ł���A�ׂ��w���ł���z��\(\small \alpha\)�̊W�� ������Ă��܂��B���̓��Ǝ�̊T�O���A ���Ƃ���1���̖{�̒P��̑����ƒP��̎�ނ̊W�ɓǂݑւ��邱�ƂŁA ���낢��ȏ�ʂœK�p�\�ł��邱�Ƃ��q�ׂ��܂��B �ȏ�̂��ƂŁA\(\small y=\ln(S+1), \mu=\ln A, \gamma=(1-\alpha)/\alpha\)�� ������ \[\small z=\frac{dy}{d\mu}=\frac{e^{\gamma y}-1}{(1+\gamma)e^{\gamma y}-1}\] \[\small a=\frac{dz}{d\mu}=\frac{\gamma^2e^{\gamma y}} {\left\{(1+\gamma)e^{\gamma y}-1\right\}^2}\] ��������A\(\small a\)��\(\small \alpha\approx 1\)�̂Ƃ��ɍő�ɂȂ�̂ŁA �ΐ��퐔(y)�̉����x���ő�ɂȂ�悤�ȃ��J�j�Y�����������Ƃ��� �W�b�v�̖@�������藧���Ƃ�������Ă��܂��B |
|
������ӂ̃X�P�[���A�b�v�F�̂��琶�Ԍn�� ���{���Ԋw��Ɍf�ڂ��ꂽ���̂ł�(2013�N)�B �����������^�����܂ŁA�����̑̃T�C�Y�Ƒ�ӑ��x�̊Ԃɂ� 3/4��ׂ̂��摥�̊W�����邱�Ƃ��m���Ă��܂��B ���̃��J�j�Y���ɂ��Č�������Ă��܂��B |
|
��`�q�����̊m�����F����̓����E�w�i�E�@�\�Ƃ̊W �A���Ȋw�őO���Ɍf�ڂ��ꂽ���̂ł�(2019�N)�B ��`�q�����ʂ̂�����ɂ͂��낢��ȃ^�C�v������A ���K���z�A���z�A�ׂ����z�ɂ��������ꍇ������悤�ł��B ��`�q�̔�������Ƀt�B�[�h�o�b�N���ʂ̉e���������Ȃ��Ƃ��͐��K���z�ɁA �t�B�[�h�o�b�N���ʂ̉e���������Ă���Ƃ��ׂ͂����z�ɂ����������Ƃ� ��������邱�Ƃ���A�����ʂ̕��z�̎d�����݂邱�Ƃ� ��������̗l���𐄑��ł���̂ł͂Ȃ����A�Ƃ������Ƃ��q�ׂ��Ă��܂��B |
|
�g�̊������n��ɂ݂铮���s���̑g�D���Ƃ��̐����@�� �u�v���Ɛ���v�̘_���ł�(2010�N)�B �l�Ԃ̊�����r���v�^�̉����x�v�ŁA �쐶�}�E�X�̊��������d�V�[�g�Z���T�[�ő��肵�āA ���ꂼ��̋x�����Ԃ̎��Ԃ̓x�����z�ׂ�ƁA �����������ׂ̂����z�ɏ]�����Ƃ��q�ׂ��Ă��܂��B |
|
�������ۂƃl�b�g���[�N �����ł́A �������ۂ��l�b�g���[�N�Ƃ��đ������ꍇ��Web�T�C�g��_���� �܂Ƃ߂��Ă��܂��B |
|
|
| �u�ׂ����z�v�ƎЉ�� |
| �����ł́A�Љ�ۂ�l�Ԃ̍s���̒��Ɍ�����u�ׂ����z�v��������Ă��� Web�T�C�g��_�������܂Ƃ߂܂����B |
|
���{�����̐��ڐG�l�b�g���[�N�ɂ̓X�P�[���t���[�������݂��� ���ەی��w�̌����Ƃ��āA �C���^�[�l�b�g�����œ��{�ݏZ�̒j�����ꂼ��2,500�l(�v5,000�l)���� �u�l���ł���܂ł̗v�̐��ڐG�l���v�Ɓu���ߎO�����Ԃ̗v�̐��ڐG�l���v �ɂ��Ē��������Ƃ���A �ǂ�������ʂɂ�炸�X�P�[���t���[���������Ƃ����������悤�ł��B ���̂��Ƃ̓��[���b�p�ł̒����ł͒m���Ă��܂������A �A�W�A���ł����l�ł��邱�Ƃ������ꂽ�悤�ł��B |
|
�T�b�J�[�̎i�ߓ����������ɍł��p�X�ɗ���ł��邱�Ƃ��Ȋw�I�ɏؖ� �T�b�J�[�I���_�Ƃ��đI��Ԃ̃p�X���}�Ƃ݂邱�Ƃɂ��A �T�b�J�[�̎�������̃l�b�g���[�N�ƌ��Ȃ��Č�������ƁA �����ɂׂ����z������邱�Ƃ�������Ă��܂�(2012�N)�B |
|
�}�N�����x���ɂ�����푈�̓��� �푈�E�����ɂ�����펀�҂̐��Ɛ푈�̕p�x���ׂ����z�ɂ��������Ă��܂��B ���̂��Ƃ����ۂ̃f�[�^�Ŋm�F������ŁA ���̃f�[�^���q�ׂɌ������邱�Ƃɂ��A �u���l���̒��̖@�����v�Ɓu�@�����̒��̑��l���v�Ƃ������_���яオ�点�A ����̉���̂��ƂɃ��f�������ăV�~�����[�V�������ʂ���������Ă��܂�(2010�N)�B |
|
���Д̔��s��ɂ�����B�ꂽ�@���� ���{�S���̏��Д̔��̎��f�[�^�����ƂɁA���낢��ȕ���̏��Ђ� �̔������Ə��ʂ̊W���ׂ��摥(�����ł́A�W�b�v�̖@��) �ɏ]���Ă��邱�Ƃ�������Ă��܂��B |
|
�ׂ��摥���m�����f���Ɖf��̓��v�f�[�^�ւ̓K�p ���i������Ă����l�q��P���������m���ߒ�����Ă���A ���Ȃׂ����z��������邱�Ƃ��Љ��Ă��܂��B ����ɁA��Ă������f�������ۂ̕��z���悭�������邱�Ƃ��A �A�����J�̉f��̋��s�����̃f�[�^��p���Č�����Ă��܂��B |
|
�l�����z�̐��ʕ��� �n���o�Ϙ_�W�Ɍf�ڂ��ꂽ���̂ł�(2017�N)�B �s�s�̐l���Ə��ʂ����ΐ��O���t�ł͌X��\(\small -1\)�̒����ɂȂ邱�ƁA �܂�W�b�v�̖@���ɂ��������Ă��邱�Ƃ� �m���ߒ��̊ϓ_���猟������Ă��܂��B |
|
���[���ɂ����{����͂̌�b�̕�Ɋւ��錤�� �d�C�ʐM���y���c��������������(No.32)�Ɍf�ڂ��ꂽ���̂ł�(2017�N)�B LINE�ŗ\���ϊ����@�\�����ĉ�b�����Ƃ��A �\���ϊ����@�\�����Ȃ��ʼn�b�����Ƃ��A ������LINE���g�p�����ɒ��ډ�b(�M�k)�����Ƃ���3�̏ꍇ�ɂ����āA ���ۂɎg�p���ꂽ�P��Ɓu�I�v�̂悤�ȋL���̏o���p�x�Ə��ʂׂāA ������̏ꍇ���W�b�v�̖@���ɏ]���Ă��邱�Ƃ�����Ă��܂��B ��b���Ԃ́A�������15���ł��B |
|
����f�[�^�ɓ��݂�����I�����ɂ��� ����ɓ��݂��鐔���I�ȕ��Ր���s�ϐ��������̂Ƃ��āA ����̃G���g���s�[�Ⓑ���ւɂ��ĉ������Ă��܂��B |
|
�W�b�v�̏��ʋK�͂̉����𐫂ɂ��� �W�b�v�̖@���̒莮���A�����@�\�A�K�p�\���A�����ē����ɂ��� �܂Ƃ߂��Ă��܂��B |
|
|
| �u�ׂ����z�v�ƌo�ό��� |
| �����ł́C�u�ׂ����z�v�ƌo�ό��ۂƂ̊ւ���������Ă���T�C�g�� �Ƃ�܂Ƃ߂܂����D |
|
���_�ƌ����̌덷�ɂ��čl����`���K���z�Ƃׂ����z�` �����̋��Z�H�w�ł͐��K���z��O��Ƃ����d�g�݂ōl���Ă������Ƃɂ��A �߂����ɂ����N���Ȃ����Z��ϓ��ɑΉ��ł��Ȃ��������Ƃ��q�ׂ��Ă��܂�(2014�N)�B |
|
���{�̍��z�[�Ŋz�ׂ̂��摥�ɂ��� �u���_�ƕ��@�v�Ɍf�ڂ��ꂽ���̂ł�(2001�N)�B ���z�[�Ŏ҂̔[�Ŋz�Ə��ʂ̊Ԃɂׂ��摥�����藧���Ă��邱�Ƃ�������Ă��܂��B |
|
���v�����w�Ō���o�ό��ۂƗՊE�h�炬 ���p�����Ɍf�ڂ��ꂽ���̂ł�(2006�N)�B �����G�����ɂ��A�o�ό��ۂ����]�ڌ��ۂ̗ՊE�h�炬�Ɠ����悤�� �����������Ă��邱�Ƃ��Љ��Ă��܂��B |
|
����̕ϓ��͐��K���z�ƈقȂ� ���o���ϊ����̕ϓ����t�[���G��͂���ƁA �u1/f�h�炬�v�ŕϓ����Ă��邱�Ƃ�������Ă��܂�(2008�N)�B |
|
�ב֎s��̓� �T���u�_�C�������h�v�Ɍf�ڂ��ꂽ�L���ł�(2009�N)�B �����H��̍��������q���ɂ��A �ב֎s��̉��i���胁�J�j�Y���ɂ��āA ���v�����w�̎�@�Ŗ��炩�ɂ���Ă������Ƃ��Љ��Ă��܂��B |
|
�o�ϕ����w�̔��� �����G�����́u�o�ϕ����w�̔����v����C 13�N�Ԃɂ킽��1�����݂̉~�h���בփ��[�g�̕ψʂ��ׂ����z�� �]���Ă��邱�Ƃ���������Ă��܂��D |
|
�o�σo�u���̐������f�����O �����Ȋw�Ɍf�ڂ��ꂽ���̂ł�(2019)�B 1986�`2015�N�Ɏ�s���Ŏ�����ꂽ���Ã}���V�����̔����f�[�^(��100����)�� �f�[�^�����Ƃɉ��i�ƕ������̊W���݂�ƁA �ׂ����z�ɏ]���Ă��邱�Ƃ�������Ă��܂��B |
|
�o�ϕ����w�̌��� �o�ϕ����w�̑n�n�҂Ƃ������ׂ������G�����̍u���ł��B |
|
���f�B�A�~�b�N�X�ɂ�����Power Law �ׂ����z�Ɍ���郍���O�e�[�������͂��ē���ꂽ�A �}�[�P�e�B���O�Ɋւ����̒m��������Ă��܂�(2009�N)�B |
|
�u���Љ�w�����v�ɂ݂�s��Љ�́u�ׂ����z�v �����r�����ɂ��u���Љ�w�����v�̘_�|���Љ��Ă��܂�(2005�N)�B ���낢��Ȃ��Ƃ��u�ׂ����z�v�ɂ��������Ă��邱�Ƃ��A ���ꂩ��̏��Љ�͂ǂ̂悤�Ɏ~�߂�ׂ����ɂ��� �_�����Ă���悤�ł��B |
|
|
|
�o�ό��ۂɂ����镪�z �s���v�ʊw�Ɍf�ڂ��ꂽ���̂ł�(1975�N)�B �S���ю����͕K�������ׂ����z�ɂ��������Ă��Ȃ����A ��Ƃ̎��Y�K�͂�]�ƈ��K�͂̕��z�ɂ͂悭���Ă͂܂邱�Ƃ��q�ׂ���ŁA �K�w�Ԃ̈ړ������ł���Ƃ���Ƃׂ����z������Ă��邱�Ƃ��Љ��Ă��܂��B |
|
��Ǝ��Y�E�����ɂ�����W�b�v�̖@�� ������w�H�w�����Ɍf�ڂ��ꂽ���̂ł�(2004�N)�B ���ۂ̊�ƃf�[�^�����ƂɊe�Ǝ�ɂ������Ǝ��Y�ɂ��� �W�b�v�̖@�������藧���Ă��邱�Ƃ��m�F������ŁA ���ȑg�D���̎��_�������ꂽJAVA�ɂ��V�~�����[�V�������s���A �W�b�v�̖@�����Č�����邱�Ƃ��m���߂��Ă��܂��B |
|
���z���ɂ��o�σ��J�j�Y���̉� ���f�^��Ȋw�Z�p�����c�̘A���̉�u �����v�Ɍf�ڂ��ꂽ���̂ł�(2013�N)�B ���Z�s��A�s���Y�s��A�Ɠd�I�����C���s��A�����s��Ȃǂ� �l�X�Ȏs��ŋ��ʂ��Ăׂ����z���ϑ�����邱�Ƃ��Љ��A ���̂悤�Ȃׂ����z������郁�J�j�Y���ɂ��Č�������Ă��܂��B |
|
��Ə����������f���Ɠ����헪 TOPIX(���؊����w��)�̉��i�ϓ��ɂ��ăt���N�^���������邱�Ƃ� ���J�ɉ������Ă��܂�(2006�N)�B �����n�łׂ����z��������̂͑��]�ڂ̂�����ՊE�_�t�߂ł��邱�Ƃ���A �o�ό��ۂłׂ����z�������͎̂��v�Ƌ����̋ύt�_�t�߂Ƃ��ė����ł��邱�Ƃ� �q�ׂ��A���낢��ȕϓ���������郂�f���Ƃ��� ����̊m���������������Љ��Ă��܂��B |
|
���{�̒n���ϓ����J�j�Y���Ɋւ���o�ϕ����w�I���� �n���̃o�u���̔������J�j�Y���Ɋւ��钲�������ŁA �����i�т̒n�����z�����ǂ낭�قǁu�ׂ����z�v�ŋߎ��ł��邱�Ƃ�����Ă��܂��B |
|
|
| �u�ׂ����z�v�ƃl�b�g���[�N |
| �����ł́A�u�ׂ����z�v���l�b�g���[�N�̕��͂Ō���邱�Ƃ�������� Web�T�C�g��_�������܂Ƃ߂܂����B |
|
�l�b�g���[�N�Ȋw �A���o�[�g�E���Y���E�o���o�V���ɂ�� 2019�N2���ɖ|��o�ł��ꂽ�l�b�g���[�N�Ȋw�̌���œI�ȋ��ȏ�(496��)�ł��B |
|
�F�B�̗F�B�݂͂ȗF�B���[���G�l�b�g���[�N�Ȋw �u���Y�����v�Ɍf�ڂ��ꂽ���̂ł�(2016�N)�B �u���G�l�b�g���[�N�v�ɂ��Ă̍u�����܂Ƃ߂����̂ł��B �l�b�g���[�N�̊�{�����ɂ��ĉ������Ă��܂��B |
|
���G�Ȋw�ƃl�b�g���[�N�`�Ȃ�����̉Ȋw�` NII�s���u���Řb���ꂽ���e�ł�(2007�N)�B �l�b�g���[�N�̊T�v�A���낢��ȕ���̂��Ƃ��l�b�g���[�N�Ƃ��đ������邱�ƁA ���̓�����\���w�W�A���̃��f�����Ȃǂɂ��ĉ������Ă��܂��B |
|
���G�l�b�g���[�N�F���v�����w�̎��_ ���������Ɍf�ڂ��ꂽ�u�`�m�[�g�ł�(2013�N)�B ���v�����w�̎��_����̕��G�l�b�g���[�N�ɂ��ĊȌ��ɂ܂Ƃ߂��Ă��܂��B |
|
���G�l�b�g���[�N�̕��� ��51�����Ă̊w�Z�ł̍u���ł�(2006�N)�B �����̎�茤���҂�ΏۂɁA���G�l�b�g���[�N�̓����ƊT�ς��q�ׂ�ꂽ��ŁA ����̃��f���ɂ��ďڂ����������Ă��܂��B |
|
�u�X���[�����[���h�v�l�b�g���[�N�̏W���I�_�C�i�~�N�X �u�X���[�����[���h�v��������b�c�E�X�g���K�b�c�_���� �O��ƂȂ�m���̉�����܂߂Ȃ���A���̘_�������ǂ������ʂ��ڍׂ� ����Ă��܂��B |
|
�X�P�[���t���[�E�l�b�g���[�N�̒� �A���o�[�g�E���Y���E�o���o�V���u�V�l�b�g���[�N�v�l�[���E�̂����݂�ǂ݉����v �̏��ǂ���l�ōs���āA���̊T�v�����Ȃ�ڂ�������Ă��܂��B �l�b�g���[�N�ɂ����āu�ׂ����z�v���ǂ̂悤�Ȍ`�Ō���Ă���̂��A �Ȃ��u�ׂ����z�v�ɂȂ�̂��̊T�v��c�����邱�Ƃ��ł���Ǝv���܂��B |
|
�X�P�[���t���[�E�l�b�g���[�N�̗��� �l�b�g���[�N�̎������z���u�ׂ����z�v�ɂȂ邱�Ƃ����� Mathematica�̃A�v���ɁC�uBarabasiAlbertGraphDistribution�v�Ƃ������̂� ����悤�ł��B���̃A�v���𗘗p�����V�~�����[�V�������A ��̓I�Ȏ菇�ƂƂ��ɏЉ��Ă��܂��B |
|
|
|
�l�b�g���[�N�̍\�� �l�b�g���[�N�̎����̕��z���ׂ����z�ɂȂ邱�Ƃ�A�ׂ����z�̓����Ȃǂɂ��� �X���C�h�ʼn������Ă��܂��B |
|
�ϑJ�𑱂���l�b�g���[�N�n�̊挒���ɂ��� ������Ɛ�含�������ł����A �����̌n�͂Ȃ����G�ȍ\�����ێ��E�����ł���̂��ɂ��āA ���G�l�b�g���[�N�̍ŐV(2018.12)�̌��ʂɊ�Â��ăX���C�h�ʼn������Ă��܂��B |
|
�l�b�g���[�N�Ȋw�ɂ�����t���N�^������ �u�l�b�g���[�N�v�Ɋւ����{�p���������x����������œǂނƁA �l�b�g���[�N���ǂ̂悤�Ȃ��̂ŁA���œ����Â����A�������ł���̂��� �̑S�̑��ɂ��ĊȌ��ɂ܂Ƃ߂��Ă��܂��B |
|
�ׂ��w����p�����C���^�[�l�b�g�o�b�N�{�[���̃l�b�g���[�N�\������ IIJ�̃o�b�N�{�[������ɂ��āA���̔N���Ƃ̔��W�ߒ�����������Ă���A ������e�ʂƏ��ʂ̊W���ǂ̔N�x�����ΐ��O���t�œ����悤�ȌX���� �ׂ����z�ɂȂ��Ă��邱�Ƃ�������Ă��܂�(2003�N)�B |
|
�X���[�����[���h�ƃ`�����X���� �l���m�\�w��_�����Ɍf�ڂ��ꂽ���̂ł��B �X���[�����[���h�Ƃ����O���t�\���ɂ��ďڂ����������Ă��܂�(2003�N)�B |
|
�_���̈��p�E�����W���牽�������邩 �d�q���ʐM�w��̐M�w�Z�@�Ɍf�ڂ��ꂽ���̂ł��B �_���̈��p�W�⋤���W���l�b�g���[�N�Ƃ��ĂƂ炦�鎖�ɂ��A �����̕��z���ׂ��摥�ɂ��������Ă��邱�Ƃ�������Ă��܂��B |
|
��ԏ�̃l�b�g���[�N�v�@�[���ȑg�D���̎l�{���𒆐S�Ɂ[ ��11��l�b�g���[�N���Ԋw�V���|�W�E���ł̍u��PPT�ł�(2014�N)�B �u�D��I�I���v�u�����N�̓����v�u�ċA�I�����v�u�����R�s�[�v�Ƃ����A ��ԏ�̃l�b�g���[�N���ȑg�D���̎l�{���𒆐S�ɉ������Ă��܂��B |
|
�������ւ������G�l�b�g���[�N�ɂ�����Z����� �R���s���[�^�\�t�g�E�F�A�Ɍf�ڂ��ꂽ���̂ł�(2011�N)�B �l�b�g���[�N�̃m�[�h�Ԃ̎������ւ��l�������ꍇ�ɁA �l�X�ȃ^�C�v�̃m�[�h�����ɂ��ăl�b�g���[�N��̋���A�������� �ǂ̂悤�ɕ��Ă������ɂ��Č�������A �X�P�[���t���[�l�b�g���[�N�ɂ�����I��I�m�[�h�����̐Ǝ㐫�� ���P�ł���\������������Ă��܂��B |
|
�W��ǂ݉�����i�Ƃ��Ẵl�b�g���[�N�̍\����� �\�t�g�E�F�A�Ɍf�ڂ��ꂽ���̂ł�(2007�N)�B ���݂ɊW�̂��镡���̗v�f����V�X�e���� �l�b�g���[�N�Ƃ��ĂƂ炦�č\������͂���ƁA �X�̕���Ɍ��肳��Ȃ����ՓI�Ȑ��������������邱�Ƃ���A ���̎��_�ŕ������Ă��邱�Ƃ��T�����āA ����𗘗p��������̖������̗Ⴊ�Љ��Ă��܂��B |
|
�V�l�b�g���[�N���_�̉\������� ���ۑ�w�O���[�o���E�R�~���j�P�[�V�����E�Z���^�[�̋@�֎��u�q��(�����傤)�v�� �f�ڂ��ꂽ�����r�����Ɗۓc�ꎁ�ɂ��Βk�����J����Ă��܂�(2003�N)�B |
|
�l�b�g���[�N���n������m�\ �R���s���[�^�\�t�g�E�F�A�Ɍf�ڂ��ꂽ2007�N�̑Βk�ł��B �l�b�g���[�N�A���ȑg�D��(�n��)�A�X�P�[���t���[�A�X���[�����[���h�A ���ݍ�p�ȂǁA���̕���̖��_����ՓI�ɗ�������Ƃ��Q�l�ɂȂ�� �v���܂�(2006�N)�B |
|
|
|
���G�l�b�g���[�N�T���[���Ԋw�ւ̉��p���������� ���{���Ԋw��Ɍf�ڂ��ꂽ���̂ł�(2006�N)�B ���G�l�b�g���[�N�ɂ��ĊT���� �H���Ԃ�`���ߒ��̗Ⴊ�Љ�ꂽ��ŁA ���Ԋw�ւ̉��p�̉\���ɂ��ċc�_����Ă��܂��B |
|
�������l�b�g���[�N�̍\����� �����n�ɂ�����l�b�g���[�N�����̊T�v�ɂ��ăX���C�h(PPT)�ʼn������Ă��܂��B �X���[�����[���h�A�X�P�[���t���[�l�b�g���[�N�A�D��I�I���^�������f���A �K�w�I�l�b�g���[�N�Ȃǂ̉��������܂��B |
|
���̓��l�b�g���[�N�\���̐������f���Ə���� ���������Ɍf�ڂ��ꂽ���̂ł�(2007�N)�B �������V�X�e���Ƃ��ė��������Ńl�b�g���[�N�Ƃ��Ă̂Ƃ炦���ɂ��� ���������ŁA�^���p�N�����ݍ�p�l�b�g���[�N�̃��f������Ă���A ���ۂ̃f�[�^�x�[�X�Ƃ����Ă͂܂��Ă��邱�Ƃ��m�F���Ă��܂��B |
|
���̕��q�l�b�g���[�N�̃g�|���W�[��� ���������Ɍf�ڂ��ꂽ���̂ł�(2006�N)�B ��`�q��^���p�N���Ȃǂ̑��ݍ�p���l�b�g���[�N�Ƃ��đ�����ƁA ���̃l�b�g���[�N�̎������z���ׂ����ɂ��������Ă��邱�ƁA �������z����ł͂Ȃ� ���ʂ┭���ʂ����l�̌X���������Ă��邱�Ƃ�����Ă��܂��B |
|
�_�o��H�Ԃɂ�����"�����Ȑ��E"�̈Ӗ� ���{�_�o��H�w��Ɍf�ڂ��ꂽ���̂ł�(2007�N)�B ������u�X���[�����[���h�v�̓������A�_�o�זE�̍זE�Ԃ̑��ݍ�p�A ���邢�͔]�̗̖�Ԃ̑��ݍ�p�̂ǂ���̊K�w�ł�������悤�ł��B |
|
�l�b�g���[�N�\���������炷���o�X�g�i�ՊE�� ���{�_�o��H�w��Ɍf�ڂ��ꂽ���̂ł�(2014�N)�B �X���[�����[���h�������l�b�g���[�N�Ɍ�����ՊE���ɂ��čl�@����Ă��܂��B |
|
�]�Ə��l�b�g���[�N�̉��f�I���� ���{�_�o��H�w��Ɍf�ڂ��ꂽ���̂ł�(2014�N)�B �]�@�\�̃l�b�g���[�N���A�O���t���_��͂𒆐S�ɉ������Ă��܂��B |
|
��Ӄl�b�g���[�N�̓X�P�[���t���[�����W���[����������
�K�w�I�l�b�g���[�N �����ɂ������Ӄl�b�g���[�N�ɂ��ẮA �o���o�V�����҂ɓ����Ă���_�������ǂ������ʂ��ڂ����܂Ƃ߂��Ă��܂��B |
|
�זE����Ӄp�X�E�F�C�̓X�P�[���t���[�E�l�b�g���[�N�ł��� 43��ނ̐����̍זE����Ӄl�b�g���[�N���A �y�f�����̊�_�A�������}�Ƃ����l�b�g���[�N�͂���ƁA ������ɂ�炸�X�P�[���t���[�E�l�b�g���[�N�̓��������������ƁA ��Ӄl�b�g���[�N�̕��ϋ����͐�����ɂ�炸�قڈ��ł��邱�Ƃ� �����_���̓��e���Љ��Ă��܂��B |
|
|
| �u�ׂ����z�v�̃��J�j�Y�� |
| �����ł́A �ׂ����z�̃��J�j�Y���ɂ��čl�@���������Ă���T�C�g�����܂Ƃ߂܂����B |
|
�ׂ����z�̃��J�j�Y�� �ׂ����z���ǂ̂悤�ȏꍇ�Ɍ���邩�ɂ��āA �l�b�g���[�N�ł̃����N�̎d�������Ƃɉ������Ă���A �����_���Ƀ����N���Ă����ꍇ�ƁA �����N���̑����Ƃ���Ƀ����N���Ă����ꍇ�Ƃ̈Ⴂ�ɂ��� Flash�Ō��邱�Ƃ��ł��܂��B �ׂ����z�͌�҂̏ꍇ�Ɍ���܂��B |
|
Barabasi-Albert���f������ׂ��w���o �l�b�g���[�N�̎������z���ׂ����z�ɂȂ邱�Ƃ����f�������� �o���o�V�E�A���o�[�g���f��(BA���f��)�ɂ��Đ��w�I�ȑ��ʂ��������Ă��܂��B �_(�m�[�h)���A�����N�������_�ƗD��I�Ƀ����N�����Ȃ��瑝���Ă����ƁA �������z���ׂ����z�ɂȂ��Ă����悤�ł��B |
|
�m�[�h���ʂɂ��I����p�����X�P�[���t���[�E�l�b�g���[�N���f�� �\�t�g�E�F�A�Ɍf�ڂ��ꂽ���̂ł�(2007�N)�B �l�b�g���[�N�̎������z���X�P�[���t���[�ɂȂ郂�f���Ƃ���BA���f�����L���ł����A �����ł͓_�𑝂₷���ƂȂ�����K���Ɋ�Â��ă����N���Ă����ƁA �������z���ׂ����z�ɂȂ郂�f������Ă���A���̃��f���Ƃ̔�r���Ȃ���Ă��܂��B |
|
�v�f�̑I�������Ɋ�Â��ׂ��摥�������f�� �K���̂Ȃ����R��Ԃł̓G���g���s�[�����債�Ă����Ƃ����z��̂��ƂɁA ���S�Ɍ��藝�͕��U�����̂��ƂŃG���g���s�[���ő�ɂȂ�̂ɑ��āA �ΐ��̊��Ғl�����̂��ƂŃG���g���s�[���ő�ɂȂ�ׂ̂͂��摥�����藧�Ƃ��� ���邱�Ƃ�������Ă��܂��B |
|
���R�⍻�u�`���ɂ�����u�ׂ��摥�v�̏o�� ���Ƙ_���Ƃ��Ă̓��e�ł�(2016�N)�B �����𗎂Ƃ������Ă����Ǝ��R�ɍ��R���`������A �X�������Ȃ�Ɛ�����������܂����A �R���s���[�^�V�~�����[�V�����ɂ�� ����̑傫���ƕp�x���ׂ����z�ɂ����������Ƃ��A ���낢��ȏꍇ�Ɋm���߂��Ă��܂��B |
|
���R�̉����f�� �u���{�����w��v�̘_���ł�(2000�N)�B ���ȑg�D���ՊE���ۂ̃��f�����ł���BTW���f�����A ���w�ʼn�͓I�ɍl�@�ł���悤�Ɉ�ʉ������f�B�[�p�b�N�E�_�[���̃��f���ɂ��� �������Ă��܂��B |
|
���Ԋw�̃X�P�[�����O���_�[�N���C�o�[�̖@���ƃt���N�^�������[ ���{���Ԋw��Ɍf�ڂ��ꂽ���̂ł�(2013�N)�B �ő̂̌ċz���x����������x�Ȃǂ̑�ӑ��x�Ƒ̃T�C�Y�Ƃ̊W�� �ׂ��摥�ɂ��������Ă��邱�Ƃ������̗�Ŏ�����Ă��܂��B ���ɁA�����̓����Ōő̂̌ċz���x���̏d��3/4��ɔ�Ⴗ��悤�� �N���C�o�[�̖@���ƌĂ�Ă��܂��B �ő̂����ȑ�������ۂ悤�Ȑ��������邱�ƁA �ő̓����̐������̎����A���l�b�g���[�N�Ƀt���N�^���������邱�ƂȂǂ� ���肵�āA���_�I�ȍl�@���Ȃ���Ă��܂��B |
|
���́A���z�����̃����L���O�ׂ͂���������̂� ���{���p�����w��N��Ŕ��\���ꂽ���̂ł�(2002�N)�B ���z�����̃����L���O���ׂ���������ȒP�����f������Ă���A ���̃��f�����ׂ���������̂̓t���N�^�����ɂ����̂ł���A �������J�j�Y���ɓ���q�\�����`������邱�Ƃɂ�邱�Ƃ�������Ă��܂��B |
|
��Ƃ̏������z�̃W�b�v�� ���ƌ����Ƃ��Ă̓��e�ł��B ��ƊԎ������Ɉ��̏��������ăV�~�����[�g����ƁA ����������Ȃ�قNJ�Ǝ��Y���W�b�v�̖@���ɋ߂Â��Ă������Ƃ� ������Ă��܂�(2001�N)�B |
|
�������f���Ƃ��̗��_�I��� ���������Ɍf�ڂ��ꂽ���̂ł�(1997�N)�B ���ϊ����̉��i�ϓ����ׂ����z�ɂ����������Ƃ��������Ă��܂����A ���̂��Ƃ����f�������āA�ׂ����z������郁�J�j�Y���ɂ��Č�������Ă��܂��B |
|
��Ə������z�ɂ�����Power-Law�������J�j�Y�� ���������Ɍf�ڂ��ꂽ���̂ł�(2004�N)�B ���ۂ̖c��Ȋ�ƃf�[�^�[��p������͂��s���Ă��܂��B �������z�ׂ̂��w����30�N�O�ƌ��݂ŕς��Ȃ��悤�ł���A �o�ό��ۂ́u���ȕϒ��v���Z�X�v�ɂȂ��Ă���悤�ł��B �����̎��Ԕ��W�ɏ�Z�m�C�Y�������U�����W���o�������������肷�邱�Ƃ� �������z���ׂ����z�ɂȂ邱�Ƃ�������Ă��܂��B |
|
��ƊԎ���l�b�g���[�N�̐������J�j�Y������ ���H��ł̌������ʍL��Ƃ��Ă̓��e�ł��B ���{��Ɩ�100���Ђ̎���l�b�g���[�N�̐������J�j�Y���͂��āA ��ƃl�b�g���[�N�̐����ɂ́A��Ƃ̐V�K�Q����|�Y�̑��ɁA �����┃���Ȃǂ̋ÏW���ʂ��d�v�Ȗ�����S���Ă��邱�Ƃ�A�������f���� �X�P�[���t���[����������ԂɎ����I�Ɏ������邱�Ƃ̏ؖ��� �Ȃ��ꂽ�悤�ł��B |
|
�g�U�����[�W �Î~���Ă���1�̗��qA�ɁAA�̉��Ńu���E���^�������Ă��闱�q���Ԃ���� A�ɂ������ĐÎ~����Ƃ��܂��B �g�U�����[�W(Diffusion-limited aggregation, DLA)�ƌĂ�܂��B ������J��Ԃ��Ă��ƍŏ��̗��qA�Ɏ��X�ɗ��q���������āA �����̌`�`����܂��B�P�Ƀ����_���ɂ������Ă��������Ȃ̂� �����ɂ͎��ȑ����`���Ȃ��t���N�^���}�`���`������A �}�̑傫���Ƃ��̑傫���̎}�̐��ׂ͂����z�ɂ��������Ă��܂��B ���L���Q�Ƃ��Ă��������B |
|
|
Tsallis���v �u�ׂ����z�v���X�̌��ۂɂƂ���Ȃ��ň������߂̐����Ƃ��� �uTsallis���v�v������܂��B ����́A���낢��ȏ�ʂŌ����w���������`���������� \(\small y'=y\) �� ���ł��邱�Ƃ���A����`���������� \(\small y'=y^q\) �̉���p���� �l���悤�Ƃ�����̂ł��B���̉�����A�w���� \(\small \exp{x}\) �� �ΐ��� \(\small \ln{x}\) �̊g���Ƃ��� \(\small q\)-�w����, \(\small q\)-�ΐ�������`����C \(\small q=1\) �̂Ƃ��͒ʏ�̊��ƈ�v���܂��B ����� \(\small q\)-�ςȂ���̂��l����ƁA �ʏ�̎w������ΐ����Ɠ��l�̐����������Ƃ�������܂��B �ڂ����́A���L���Q�Ƃ��Ă��������B |
|
|
| ���]�ځE�ՊE���� |
�ׂ����z��ׂ��摥�́A�C�̂��t�̂ɂȂ����肷��ȂǁA
�����̗l�������I�ɕς���Ă��܂����]�ڂ̋��E�t�߂ł�����Ă��܂��B�����ł́A
���̑��]�ڂ⋫�E�t�߂ł�����ՊE���ۂɂ��ĉ�����Ă���
Web�T�C�g��_�������܂Ƃ߂܂����B
|
|
���]�ړ��� ������w���w�������w�Ȃ̊w���L�u�ɂ��A �u���]�ځv�ɂ��ē���I�ȉ��������Ă���A �ڂ�������ɂ������N���\���Ă��܂��B |
|
���]�ڂƗՊE���ۂ̓��v�����w �w�K�@��w�̓c��搶�ɂ��A���]�ڂƗՊE���ۂɂ��� �ŋ߂̐��ʂ܂ŃX���C�h�ʼn������Ă��܂��B YouTube�ł̉���́u�������v�ł��B |
|
�u���������v�ւ̑��]�ڇ@ ���{�Ȋw�����ق̌������ɂ��A2016�N�m�[�x�������w�܂���܂��� �u�g�|���W�J�����]�ځv�ɂ��ĉ������Ă��܂��B |
|
���]�ڂ̓��v�͊w ��B��w�ł̍u�`�^�ł�(2019�N)�B ���]�ڌ��ہA���Ϗꗝ�_�A�X�P�[�����O�����A�J�荞�Q�Ȃǂɂ��� ���I�ȉ�����Ȃ���Ă��܂��B |
|
�ՊE���ۂƌJ�荞�Q ���{��w��w�@���H�w�����Ȃ̍u�`�^�ł�(2019�N)�D �ՊE���ۂ̕��Ր����J�荞�Q�̊ϓ_����������Ă��܂��B ���I�ȓ��e�ł����A ��1�͂��u���ƂȂ��v���߂�ΑS�̑���c�����邱�Ƃ��ł���ł��傤�B |
|
�X�P�[�����O���_�Ƃ͉����H ���{�_�o��H�w��Ɍf�ڂ��ꂽ���̂ł�(2007�N) �X�P�[�����O���_�ɂ��ĉ������Ă��܂��B |
|
���x�s��J�荞�Q�ɂ��ÓT�X�s���n�̗ՊE���ۂ̉�� �_�ˑ�w�ł̊w�ʘ_���ł�(2008�N)�B ��啪��̘_���ł����A�o������20�Œ��x�ŗՊE���ۂɊւ��� ���̎��_�Ŋ��m�̓��e���܂Ƃ߂��Ă���A �ՊE�w���̊Ԃ̊W��(�X�P�[�����O��)��������Ă��܂��B |
|
�H�i�̕����Ɛ� ���{�H�i�Ȋw�H�w���Ɍf�ڂ��ꂽ���̂ł�(2015�N)�D ���ɒ��a10�`1000nm�̗��q�����U���Ă���n�C�h���R���C�h���A ��������S�������]���̏�Ԃ�A�����q�����ݍ����Ēe�������Q���� ��Ԃɑ��]�ڂ��錻�ۂɂ��ďڏq����Ă��܂��B ���]�ڂ̋ߖT�ł́A�]���̔S�x��Q���̒e�������Z�x���ׂ̂���� ��Ⴗ��W������悤�ł��B |
|
�Q�������_�̐V�������_ �M�d���������Ɍf�ڂ��ꂽ���̂ł�(1982�N)�D �����q���̃Q�����ߒ����A �p�[�R���[�V�������_�����ƂɗՊE���ۂƂ��đ����������������邱�ƁA ���̔w�i�E�T�v�E�ՊE�w���ɂ��āA���̎��_�ł̌��Љ��Ă��܂��B |
|
�����q���̂�炬 �����q�Ɍf�ڂ��ꂽ���̂ł�(1982�N)�D �����q�n�t�ł̗ՊE���ۂɂ��āA ���������L�[���[�h�ɂ��ĉ������Ă��܂��B |
|
���]�� �uNetsu Sokutei�v�Ɍf�ڂ��ꂽ���̂ł�(2002�N)�D ���x��ς����Ƃ��ɋN���鑊�]�ڂɂ��ďڂ����������Ă��܂��B |
|
�t���̗ՊE�M�ُ� �uNetsu Sokutei�v�Ɍf�ڂ��ꂽ���̂ł�(2005�N)�D �t���́A���̕��q�̂���������鉷�x�����ɑ傫���ω�����悤�ł��B ���̑��]�ړ_�̋ߖT�ł̂��낢��Ȍ��ۂɂ��ĉ������Ă��܂��B |
|
�f�B���b�N�d�q�n�ɐ��ޕ��Ր������� �����w�������̌����ł�(2016�N)�B ��K�͂ȃV�~�����[�V�����ŁA ��������≏�̂ւ̑��]�ڂɂ�����ՊE�w�������肵�����Ƃ�����Ă��܂��B |
|
"����"�������̓d�q�����������Ώ̐��w���`�s�ϐ��x�𐢊E�ŏ��߂Ď��� �����w�������ɂ�����2007�N�̃v�������[�X�ł��B 2������Ԃ̋���-�≏�̓]�ڂ𐔒l�V�~�����[�V�����ɂ�茟�����邱�Ƃɂ��A ���]�ړ_�ł͎��ȑ����\�����݂��A�p�x��ς��Ȃ����`�ϊ��ŕs�ςł��邱�Ƃ� ���������Ƃ�����Ă��܂��B |
|
|
| �p�[�R���[�V����(�Z�����_) |
�����ł́A���]�ځE�ՊE���ۂ̃��f�����Ƃ��čl�Ă��ꂽ
�p�[�R���[�V����(�Z�����_)�ɂ��čl�@���������Ă���T�C�g�����܂Ƃ߂܂����B�p�[�R���[�V�����́A���w�ł͊m���_�̖��ł���A
2006�N�E2010�N�E2022�N�̃t�B�[���Y�܂́A
�p�[�R���[�V�����̌����҂ɂ��^�����Ă��܂��B
|
|
�p�[�R���[�V���� �������ȑ�w�̐搶�ɂ��u�p�[�R���[�V�����v�Ɋւ���u�`�m�[�g�ł��B |
|
�p�[�R���[�V������� �M�`���̗��ꂩ��A�p�[�R���[�V�����ɂ��Ă킩��₷���������Ă��܂��B �u�[����[�܂Ōq����N���X�^�[������v���Ƃ̍H�w�I�ȈӖ����c���ł��܂��B |
|
�Z�����_�ƃC�I���`�� �������̃C�I���`���̗��ꂩ��A �p�[�R���[�V�����̊T�O�ɂ��Ă킩��₷���������Ă��܂��B |
|
�͂ꑐ�ۂ��ՊE���ۂ��g���ēd�C�𗬂��b �͑��ۂ̍זE�W�c�́A�p�[�R���[�V�����Ƃ����ՊE���ۂ𗘗p���� �����I�ɓd�C�I�ʐM����Ƃ������Ƃɂ��āA������₷���������Ă��܂��B |
|
�Z�����_�ւ̗U�� �����w��Ɍf�ڂ��ꂽ���̂ł�(1979�N)�B �����w�̂��낢��ȏ�ʂł̐Z�����_�̉��p�ɂ��ĉ������Ă��܂��B |
|
���̐��ߓn�����T�C�R���Œ��ׂĂ݂悤 �u��18���������됔�w�����v�ł̍u���ł�(2013�N)�B �����̓��{���w��������A ���w����ΏۂƂ��āu�p�[�R���[�V�����v�ɂ��ĉ�����Ă��܂��B �Ȃ��A�Q�n�������s�͊֍F�a�̏o���n�ł��B |
|
Percolation �ȒP�ȏꍇ�ɂ��ăp�[�R���[�V�����̉�����Ȃ���A ����̊i�q�ł̐Z��臒l�̒l���܂Ƃ߂��Ă��܂��B�܂��A \(\small d=3\) �̃x�[�e�i�q�̏ꍇ�ɁA �i�q�_��������̃N���X�^�[�Ɋ܂܂��m�����v�Z����Ă��܂��B |
|
�p�[�R���[�V�����̌J�荞�Q�V�~�����[�V���� ���Ƙ_���Ƃ��Ă̓��e�ł��B 2�����̐����i�q�̃T�C�g�p�[�R���[�V������p���āA �J�荞�Q�̑�����R���s���[�^�[��ōČ����āA �ՊE�m����t���N�^�����������߂��Ă��܂��B |
|
�Q�����ƃQ���\�� �����q�Ɍf�ڂ��ꂽ���̂ł�(1988�N)�D �]��-�Q���]�ڂɊւ��āA�p�[�R���[�V�������f���Ƃ̊֘A����������Ă���A �Q���̒e�����̗ՊE�w�������Ր��������Ƃ������I�Ɏ�����Ă��܂��B |
|
�R�Ė��ւ̃p�[�R���[�V�������_�̉��p ���{�R�Ċw��Ɍf�ڂ��ꂽ���̂ł�(2011�N)�D �����R�Ăɂ��ăp�[�R���[�V�������_�̗��ꂩ��l�@����Ă��܂��B |
|
�p�[�R���[�V�������_��p�����s�X�n�̖h�А��]�� �u�I�y���[�V�����Y�E���T�[�`�v�Ɍf�ڂ��ꂽ���̂ł�(2002�N)�D �s�X�n�̉��Ċ댯�̕]�����@�Ƃ��ăp�[�R���[�V�������_���p�����A �����s�̃f�[�^�ʼn�͂��Ȃ���Ă��܂��B |
|
�}�O�}�̃K�X�Z������͂ɂ�����p�[�R���[�V�������_�̖��� ��z���Ȋw�Ɍf�ڂ��ꂽ���̂ł�(2006�N)�B �}�O�}�̃K�X�Z�������p�[�R���[�V�������_�����p���邱�Ƃʼn�͂��悤�Ƃ��Ă���A �ŏ��Ƀp�[�R���[�V�������_�̉�����Ȃ���Ă��܂��B |
|
�p�[�R���[�V�������_�Ƃ��̐��܊J���ւ̐V�W�J �����Ђł̍u���ł�(2012�N)�B ���܊J���ɂ�����p�[�R���[�V�������_�̉��p�Ⴊ�������Ă��܂��B |
|
�p�[�R���[�V�������_�����p�����R�~���j�e�B�̏��`�����f���̍쐬 �l���m�\�w��ł̔��\�\�e�W�ł�(2019�N)�B �l�X�̏��̎�e�Ɣ��M��Z�����ۂƂ��Ċm���I�ɑ����邱�Ƃɂ��A ���̓`���m���ƖY�p�m����ݒ肷�邱�Ƃɂ����`�����f������������Ă��܂��B |
|
|
| ���G�n�E�t���N�^�� |
| �����ł́A���G�n��t���N�^���ɂ��ĉ�����Ă��� Web�T�C�g��_�������܂Ƃ߂܂����B |
|
���G�n���킩�� �u���G�n�v�Ɋւ��ĉ�������p���t���b�g�ł��B �u���ݍ�p�v�u�n���v�u�_�C�i�~�N�X�v�u���ȑg�D���v �u�K���v�u�w�ې��v�u�l�@���@�v�ɂ��ĊȌ��ɉ������Ă��܂��B |
|
�t���N�^���̘b ���X�Ɋg�債�Ă����Ă������}�`������鎩�ȑ����������� �u�t���N�^���}�`�v�ɂ��ďڂ�����������Ă��܂��B |
|
���������ƃt���N�^�� �u�t���N�^���v�Œ����ȍ����G���搶�̘_���ł�(1992�N)�B�����w�Ƃ̊ւ��ɂ��āA �R���p�N�g�ɂ܂Ƃ߂��Ă��܂��B |
|
�t���N�^���̕��� ���������Ɍf�ڂ��ꂽ�����G���搶�̘_���ł�(1985�N)�B �t���N�^���������n�߂����̑����I�ȓ��e(95��)�ɂȂ��Ă��܂��B |
|
�t���N�^���Ƃ� �u�t���N�^���v�Ɋւ��鑍���I�ȃ����N�W�ł��B |
|
�����̐X �l�u���O�ł��B�u���E��3�̃V�X�e���łł��Ă���v�Ƃ��āA �u���ȑg�D���v�u�ׂ��摥�v�u�t���N�^���v�ɂ��ĉ������Ă��܂��B �����̂��Ƃɂ��Ă�����x�̒m������ŁA ���Ԃɓǂ�ł����Ɨǂ��ł��傤�B |
|
|
| ���ȑg�D���ՊE���� |
| ���R�E�Ɍ����t���N�^���Ȍ��ۂ́A �Ȃ������]�ڂ̗ՊE�����̋߂��Ɏ��R�ɗ��������Ă����悤�ł��B�����ł́A ���̂悤�ȁu���ȑg�D���ՊE���ہv�ɂ��ĐG��Ă���Web�T�C�g�� �_�������܂Ƃ߂܂����B |
|
���ȑg�D���Ɛi���̘_�� �X�`���A�[�g�E�J�E�t�}���ɂ�铯���̏��Ђɂ��ẮA �ڍׂȓǏ��^�ł��B |
|
���ȑg�D���ՊE���ۂƁu�i���v �k�C����w�̌o�ϊw�����Ɍf�ڂ��ꂽ���̂ł�(2000�N)�B �X�`���A�[�g�E�J�E�t�}���ɂ�鎩�ȑg�D���ՊE���ۂƂ��Ă̑������̗v�_�� ������ꂽ��ŁA�u�o�σV�X�e���v���͂ւ̉��p�\���ɂ��čl�@����Ă��܂��B |
|
���R�������̃��f�� ���ȑg�D���ՊE���ۂ̗�Ƃ��ėL���ȁu���R���������f���v�ɂ��ĉ������Ă��܂��B |
|
���ȑg�D���ՊE���ۂƉ����R�͌^ ������w���H�w���̍��������搶�ɂ��28���̃X���C�h�ʼn������Ă��܂��B |
|
���G�n��̖͂ړI ���É���w�ł̍u�`�X���C�h�̂悤�ł��B �u���G�n�Ƃ́v�u���ȑg�D���v�u�J�I�X�̉��v�u���G�K���n�v�u���G�n�̊�b�����v �Ȃǂɂ��ĉ������Ă��܂��B ���ɁA�u���ȑg�D���v�̎��Ⴊ�����Љ��Ă��܂��B |
|
�n�k�Ǝ��ȑg�D���ՊE���� ���������Ɍf�ڂ��ꂽ���̂ł�(1991�N)�B ���낢��Ȏ������ʂȂǂ𑍍����āA�n�k�Ɍ��炸�A �ΎR�A�n�`�A�C��A�����́A�F���̍\�����A ���R�͈��萫�ƕq���������ˎ��������I�ȑ��]�ړ_�Ɏ��ȑg�D������Ă���Ƃ��� �l����������Ă��܂��B |
|
���I�p�[�R���[�V�����]�ڂƎ��ȑg�D���ՊE���� ���������Ɍf�ڂ��ꂽ���̂ł�(1991�N)�B ���R���������f��(BTW���f��)�̊T�v�ɂ��Đ������ꂽ��ŁA �R���s���[�^�[�V�~�����[�V�����̌��ʂ��������Ă��܂��B 4�u���b�N�ŕ����Ƃ����ꍇ�A���Ԃ��o�ɂ�A �X�̃u���b�N�̍������قڈ��̒���ԂɂȂ��Ă����l�q�Ȃǂɂ��� �������Ă��܂��B |
|
���R�̗ՊE��Ԃ̉𖾂���n�k�̗\���@��T�錤�� ���e��������p��������p���āu���R�������v�̎������s���A �ՊE��Ԃ̗l�q�����e���ʐ^���B�邱�Ƃɂ��A�����̉��͍��̗l�q�̕ω��ɂ��� ��������Ă��܂��B |
|
�A��������p�������G�n�̃V�~�����[�V���� �v����������w��k�x���̌����W��Ŕ��\���ꂽ���̂ł�(2000�N)�B ���^���o�b�^�̑唭���ɂ��ĕϓ��i�q��̊m�����f����p���� �V�~�����[�V�������s���A���Ԃ̌o�߂ƂƂ��ɒ���Ԃ� �������鎩�ȑg�D���ՊE���ۂ����������Ƃ�����Ă��܂��B |
|
|
| �V�~�����[�V���� |
| �����ł́A�l�b�g���[�N�╡�G�n���V�~�����[�g�������̃v���O������ �܂Ƃ߂܂����B |
| �l�b�g���[�N�`��\�t�g�uPajek�v |
| �l�b�g���[�N��`�悷��t���[�\�t�g�Ƃ��āuPajek�v������܂��B ���L�ɁA����Ɋւ���Web�T�C�g�����܂Ƃ߂܂����B |
|
|
���G�n�̃V�~�����[�V����-Swarm ���G�n�̃V�~�����[�V�����\�t�g�Ƃ��āuSwarm�v�Ƃ����\�t�g������悤�ł��B |
|
|
���G�n�̓���̏Љ� ���ȑg�D���ՊE���ۂ̃��f���Ƃ��ėL���ȁu���R�����v(SandPile���f��)�� �V�~�����[�V�����v���O�������_�E�����[�h���邱�Ƃ��ł��܂��B �������A���O�ɁuMicrosoft XNA Framework Redistributable 4.0�v�� �C���X�g�[������K�v������悤�ł�(�Q��)�B |
|
�ȒP�ȃp�[�R���[�V�����̃V�~�����[�V�����v���O���� EXCEL VBA��ŁA10�~10��2�����i�q�ŁA�p�[�R���[�V�������V�~�����[�g�ł��� �v���O���������J����Ă��܂��B�i�q����m����ς���A���낢��ȏꍇ�� �V�~�����[�g���邱�Ƃ��ł��܂��B |
|
|
| �Q�l���� |
�����ł́A�ׂ����z�A���]�ځA�ՊE���ہA�p�[�R���[�V�����A������
���ȑg�D���Ɋւ����ȕ�����N�㏇�Ɋ���Љ�Ă����܂��B
�Ȃ��A�w���T�C�g�ւ̃����N�͒���܂���ł����B
|
|
|