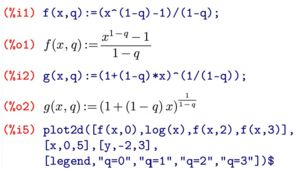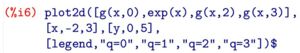「Maxima」を活用して数学の学習ロードを駆け抜けよう!
(注) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
| ■ 数式処理ソフト「Maxima」を活用した数学学習 [Map] |
|
| ||||
|
| ||||
| [御案内] 「Maxima」(マキシマ)は,フリーの数式処理ソフトです. 有料の Mathematica や Maple に劣らないレベルの数式処理が可能であり, Linux,Windows,MacOSのみならず,Android版もあります. ここでは,数学学習での Maxima の活用法について解説します. | ||||
|
[お知らせ] スマホ(Android)版Maximaの解説本を出版しました. 計算問題やグラフの確認をするときに非常に重宝します. フリーソフトなので一度試してみてください. PC版のコマンドレファランスとしても利用できます。
| ||||
|
| ||||
| ■数学学習での活用 |
|
|
| グラフ描画 |
|
冒頭の例示画面で紹介したように,
Maximaでも関数のグラフを描画することができます.
描画ツールにはgnuplotが使われていますが,
コマンドの書式が少し違うので注意してください.
|
[参考1] Maximaのグラフ描画を極めたいときは,「Maximaでお絵かき」を参照してください. ただし,タイトルは易しそうですが,内容は全く初心者向きではありません. Maximaやgnuplotについて,あるレベル以上の方でないと読みこなせないと思います. |
|
■複数のグラフ 複数のグラフを描画するには,\(\small [f(x), g(x)]\) などと 関数を書き並べて指定します. たとえば,\(\small y=x^3-2x+1\) と \(\small y=2x\) のグラフを描画するには 次のようにします.下記では最後は「$」として, グラフ画面を閉じたときにファイルが保存されないようにしています. グラフ画面を閉じると「Busy」の表示は消えます. 色の指定は,デフォルトでは,青(blue),赤(red),緑(green),マジェンタ(magenta), 黒(black),シアン(cyan)の順に色づけがなされます. 色の指定を変更したいときは,次の項目を参照してください. \(\small y\) 座標の範囲は, \(\small x\) 座標に指定した範囲から自動的に計算されます. \(\small y\) 座標の範囲も指定したいときは, 同じ書式で [y, c, d] のように追加指定します. デフォルトでは横軸のラベルとして「\(\small x\)」が付され, 縦軸には何も付されません.下図はラベルの上部を切り出したものです. グラフ画面を消すと「busy」という表示も消えます.グラフ画面を消さないと, 次のコマンドを実行することはできません. |
|
|
|
■グラフ画面の諸設定 |
|
線種 関数 \(\small y=f(x)\) のグラフは,デフォルトでは実線で描画されます. 実際には,\(\small x\) の値を少しずつ変えながら \(\small y\) の値を計算して, 隣り合う点 \(\small (x,y)\) を線で繋いでグラフが描画されています. その描画の仕方を指定するオプション変数が「style」です. デフォルトでは [style,lines] という指定が省略されていることになります. 「lines」の箇所を「dots」にすると点線で描画されます. 複数のグラフを実線と点線で描画するには次のようにします. 最初の関数のグラフが実線(lines)で,2番目が点線(dots)で描画されます. なお,下記ではコマンドの全体像が分かるように改行して示しています. TexMacs+Maximaでは「Shift+Enter」により, wxMaximaでは「Enter」により改行することができます. それぞれで,実行コマンドと改行コマンドが逆になっているので注意してください. この図では,点線の点の大きさが気になるかもしれません. その点の大きさを指定したいときは「dots」を「points」にすると, 点の大きさを指定することができます.たとえば,次のように指定すると, 点の大きさが少し大きくなります.数値は,点の大きさの半径です. 実線の太さを調整するには,lines の後で太さの数値を指定します. 下図では,線を少しずつ太くしています.数値を大きくするほど太くなります. |
|
|
|
色 色の指定は,オプション変数の「color」を利用します. デフォルトでは,青(1:blue),赤(2:red),緑(3:green),マジェンタ(4:magenta), 黒(5:black),シアン(6:cyan)の順に色づけがなされ,この順に循環します. たとえば,最初のグラフは黒で,次は緑で描画するには 次のようにします. |
|
凡例 関数が1つだけの場合は関数の式が縦軸の外側に表示されますが, 2つ以上のグラフの場合は右上にまとめて表示されます. その部分を「凡例」といいます.その書式を指定するには, オプション変数の「legend」を使用します. 最初に指定した関数の順に,右上に表示させたい語句を " " で 囲んで指定します.TeXmacs+Maximaでは日本語を入力できませんが, wxMaximaでは日本語も入力することができます. 下記は,wxMaximaによるものです. 凡例を表示させないようにするには, [legend, false] とします(図は略). |
|
|
|
軸のラベル 座標軸のラベルは, デフォルトでは横軸に \(\small x\) が付されます. 関数が1つだけの場合は縦軸に関数の式が表示されますが, 複数の関数を描画したときは, 縦軸には何も表示されません. かわりに,凡例の箇所に関数の式と色が表示されます. \(\small x, y\) だけの場合はそれでも良いですが, 具体的な内容を持つグラフの場合は,その内容も表示しておきたいところです. それらは,「xlabel」「ylabel」により指定することができます. |
|
|
|
座標軸 デフォルトのグラフ画面では目盛りが外枠に表示され, 座標軸は点線で表示されるようになっています. 外枠が表示されないようにするには [box,false], 座標軸を実線で表示させるには [axes, solid] を指定します. [box, false] を指定すると座標軸へのラベルは付されないので, 必要であれば 「label」を使用して必要な箇所に配置します. |
|
軸の目盛り 座標軸の目盛りは自動的につけられます. その表示の仕方を指定するには, 「xtics」「ytics」を使用します. xtics の書式は,[xtics, 初期値, 増分, 最終値] です. たとえば,\(\small -2\leq x\leq 2\) を1刻み, \(\small -3\leq y\leq 5\) を2刻みとするには次のように指定します. |
|
|
|
■媒介変数表示 媒介変数で表示された関数のグラフを描画することもできます. 媒介変数で \(\small x=f(t), y=g(t), a\leq t\leq b\) のグラフを 描画するには,plot2でオプション変数「parametric」を 利用して \(\small [{\rm parametric},f(t),g(t),[t,a,b]]\) と指定します.単位円の場合は,次のようになります. 「plot2d([parametric,cos(t),sin(t),[t,0,2\(\small *\)%pi]], same_xy)$」 または,縦幅を横幅の60%程度にすると縦横の比率が揃うので,たとえば「plot2d([parametric,cos(t),sin(t),[t,0,2\(\small *\)%pi]], [x, -2, 2], [y, -1.2, 1.2])$」 として軸の範囲を指定することもできます. 下図は,「same_xy」を指定した場合のグラフです. |
|
|
|
■3次元のグラフ
z=f(x,y)のグラフ 基本的にgnuplotで描画可能なものはMaximaでも描画可能です. さらには,Maximaの数式処理機能を用いることにより, たとえばマンデルブロー集合を表示させるコマンドも用意されています. マニュアルの12.3節に例示されている コマンド「mandelbrot」を実行すると下図が表示されます. 数十年前,BASICプログラムでこの画面を得るには, PCを一晩放置しておく必要がありました.現在は,ほぼ数秒で表示されます. |
|
|
|
媒介変数表示 平面上の曲線は, 媒介変数$t$を用いて \(\small x=f(t), y=g(t)\) の形で表すことができます 空間の曲面でも同様に, 曲面上の点 \(\small (x,y,z)\) が変数 \(\small u, v\) の関数として \[\small x=f(u,v),\quad y=g(u,v),\quad z=h(u,v)\] と表される場合を考えると, 関数 \(\small z=f(x,y)\) のグラフでは表すことのできない 多彩な曲面を表すことができます. \(\small u, v\) を媒介変数といいます. この変数に他の変数を使用することはできません. このような曲面を描画するには,plot3dを利用して 「plot3d ( [f(u,v), g(u,v), h(u,v)], [u, a, b], [v, c, d] )」 とします. たとえば,中心が原点にある丸いドーナツ状の曲面は, 媒介変数 \(\small u, v\) と定数 \(\small r, s\) を用いて \[\small \begin{cases} x=(r+s\cos{v})\cos{u}\\ y=(r+s\cos{v})\sin{u}\\ z=s\sin{v} \end{cases}\] により表されます.このような曲面は「トーラス」と呼ばれます. 下図は,\(\small r=3, s=1\) のときのドーナツ状曲面です. 式が長いので,あらかじめリストで式を定義しています. また,3つの軸のスケールを同じにするために「same_xyz」を追加しています. [legened, false]は,右上に式が表示されるのを抑制するためのオプション変数です. |
|
|
|
球座標 平面上における極座標と同じ考え方をすることにより, 空間内の点も原点からの距離と半直線からの角度を利用して表すことができます. 各点を下図のように定め, 点Pと原点との距離を \(\small r\) , OPと \(\small z\) 軸の正の側からの角を \(\small \theta\),そしてOP\(\small '\)と \(\small x\) 軸の正の側からの角を \(\small \varphi\) とすると,点Pの座標 \(\small (x, y, z)\) は次の式で表すことができます.ここで,\(\small r\) は \(\small r\ge 0\) , \(\small \theta\) は \(\small 0\le \theta\le \pi\), そして \(\small \varphi\) は \(\small 0\le \varphi\lt 2\pi\) とします. \(\small \begin{align*} x&={\rm OA}={\rm OP}'\cos\varphi\\ &=r\sin\theta\cos\varphi\\ y&={\rm OB}={\rm AP}'={\rm OP}'\sin\varphi\\ &=r\sin\theta\sin\varphi\\ z&={\rm OC}=r\cos\theta \end{align*}\) \(\small \begin{cases} x=r\sin\theta\cos\varphi\\ y=r\sin\theta\sin\varphi\\ z=r\cos\theta \end{cases}\\ \small \begin{cases} r=\sqrt{x^2+y^2+z^2}\\ \tan\theta=\frac{\sqrt{x^2+y^2}}{z}\\ \tan\varphi=\frac{y}{x} \end{cases} \) 球座標を利用して曲面が \(\small r=f(\theta, \varphi)\) の形で表されるとき, そのグラフをplot3により描くには, 「plot3d ( f(theta, phi), [theta, 0, \%pi], [phi, 0, 2$*$\%pi], [transform_xy, spherical_to_xyz], same_xyz )$」 とします. ただし,\(\small r\lt 0\) のときは点 \(\small (|r|, \theta+\pi, \varphi)\) を 表すものとします. オプション変数「transform_xy」の値は,標準では「false」になっています. この変数の値を「sherical_to_xyz」に指定することにより, 球座標を直交座標に直して曲面が描画されます. 「same_xyz」を指定することにより,3つの座標軸のスケールが同じになります. 下図では,球座標で \(\small r=\sin\theta\) と表される曲面が描画されています. [legend, false] とすることで,右上に表示される凡例の表示を省略しました. 「xtics」などを指定することにより, 座標軸の目盛りを0.5刻みにしています. この式を平面の極座標で考えると \(\small x\) 軸に接する円ですが, 空間の極座標では \(\small z\) 軸に接する円を回転したグラフになります. |
|
|
|
陰関数 原点を中心とする半径 \(\small a\) の球上の点 \(\small (x,y,z)\) は, 原点からの距離が常に一定であるので \(\small x^2+y^2+z^2=a^2\) を満たします. これが,直交座標による球の方程式です. この式を変形すると \(\small z=\pm\sqrt{a^2-x^2-y^2}\) となるので, \(\small z=f(x,y)\) の形の式が2つ含まれています. 一般に,変数の間の関数関係を表す式が \(\small F(x,y,z)=0\) の形の式で表されるとき,そのような関数を陰関数といいます. 陰関数(2変数関数)のグラフを描画するには専用のパッケージを読み込む必要があり, 最初に「load(draw)」を実行します. 描画コマンドは「draw3d」です. 「draw3d」により \(\small F(x,y,z)=0\) の \(\small a\le x\le b, c\le y\le d, e\le z\le f\) におけるグラフを描画するには 「draw3d ( implicit ( F(x,y,z)=0, x, a, b, y, c, d, z, e, f ) )」 と指定します.「plot3d」の書式と違うので気をつけてください. 「draw3d」では,変域を[ ]で囲う必要はありません. 下図は球 \(\small x^2+y^2+z^2=1\) を描画しています. 同様にして,下図は \(\small x^2+y^2-z^2=1\) と \(\small x^2+y^2+z^3=1\) のグラフです. |
|
|
|
■ファイル保存 Maximaで描画したグラフを保存して別な箇所でも利用したいときがあります.
ファイル保存 コマンドの末尾を「;」で終えると, 以前のバージョンでは 「c:/users/ログイン名/」のフォルダーに 「maxout12345.gnuplot」のようなgnuplotで読み込み可能なファイルで 自動保存されましたが, 最近のバージョンでは隠しフォルダーである 「c:/users/ログイン名/AppData/Local/Temp」に 保存されるようです. フォルダーの変更は「保存フォルダー」 を参照して下さい.また, 媒介変数の箇所も参照してください. |
|
|
|
ファイル形式 Maximaでのグラフ表示はgnuplotを利用しているので, デフォルトのファイル形式はgnuplotで読み込み可能な 「maxout****.gnuplot」という形のファイルになっています. その他の保存できるファイル形式には, PNG, PDF, PSの3種類の形式があります. それぞれ,[png_file,"ファイル名.png"],[pdf_file,"ファイル名.pdf"], [ps_file,"ファイル名.ps"] という形で指定します. 下記では,PDFファイルとして保存しています. 外部ファイルへの出力を指定しているので画像は表示されませんが, 古いバージョンでは「c:/users/ログイン名/」に, 最新版では「c:/users/ログイン名/AppData/Local/Temp」(隠しフォルダー)に, 拡張子が「.gnuplot」のファイルとともに保存されます. 保存フォルダーの変更の仕方は,次の項目を参照して下さい. |
|
保存フォルダー 画像ファイルのような一時的なファイルの保存フォルダーは 「maxima_tempdir」に記録されています. デフォルトの保存先は, 古いバージョンでは「c:/users/ログイン名」に, 最新版では「c:/users/ログイン名/AppData/Local/Temp」に設定されています. 「AppData」は隠しフォルダーなので,フォルダーの扱いに慣れていないと 悩んでしまうかもしれません.保存先がどこになっているかは, 「maxima_tempdir;」を実行してみるとよいでしょう. その内容を書き換えれば自分の希望するフォルダーに保存することができます. 下記では,「documents」フォルダーに変更して,さらに ファイル形式をPNGにしています. フォルダー名の最後に「/」をつける必要はありません. 変更後は,指定したフォルダーに拡張子がPNGのファイルと,gnuplotのファイルが 保存されます.PNGの方は指定したファイル名で保存されますが, gnuplotの方はmaxoutで始まるmaximaにより自動的につけられたファイル名で 「maxout****.gnuplot」のようなファイル名になります. このファイルは,gnuplotで読み取ることが可能です. |
|
TeXでの利用 TeXで利用可能なファイルとして出力するには, 旧来方式ではPS形式で保存してghostscriptを利用することになりますが, 近年は直接pdfで出力した方が良いようです. 出力の仕方は,前述のとおり, PDF形式で保存する場合は [pdf_file,"ファイル名.pdf"] を, PS形式で保存する場合は [ps_file,"ファイル名.ps"], または [ps_file,"ファイル名.eps"] とします. 得られたPDFまたはPS,EPSファイルは, TeXのソースファイルのプリアンブルで 「\usepackage[dvipdfmx]{graphicx}」の指定をして, 本文で 「\includegraphics{sanji.eps}」 などとすれば図が得られます. DVIOUTでは図が表示されませんが, dvipdfmxを利用してPDFに変換するときちんと表示されます. |
|
|
| いろいろな関数 |
|
|
|
連続ではない点や微分可能ではない点を含む関数を扱う必要が
あるときもあります.たとえば,フーリエ解析では,
そのような関数が頻出します.
■単位ステップ関数 \[\small {\rm signum}\,(x)= \begin{cases} -1 & (x\lt 0)\\ 0 & (x=0) \\ 1 & (x\gt 0) \end{cases}\] 下図は,「plot2d(signum(x),[x,-3,3],[y,-2,2])$」によるものです. 単位ステップ関数を利用すると, 適当な関数のグラフから指定した部分を切り出すことができます. たとえば,関数 \(\small f(x)\) のグラフから \(\small [a, b]\) の 部分を切り出すには,\(\small f(x)\) に次のような関数を掛けることになります. \[\small \begin{cases} 0 & (x\leq a)\\ 1 & (a\lt x\leq b)\\ 0 & (b\lt x) \end{cases}\] この関数は,単位ステップ関数を利用すると \(\small a\lt b\) として 「unit_step(x-a)-unit_step(x-b)」により表されます. 下図では,その関数を「cut(x,a,b)」と定義して, 「cut(x,-1,1)」のグラフを描画しています. |
|
|
|
■ガンマ関数 ガンマ関数 \(\small \Gamma(x)\) は, 統計学や工学で頻出する重要な関数で,次の広義積分で定義されます. \[\small \Gamma(x)=\int_0^{\infty}t^{x-1}e^{-t}\,dt\] 一般論では \(\small x\) は複素数ですが, ここでは実数で考えます. ガンマ関数には次の性質があります. \[\small \Gamma(1)=1,~ \Gamma(x+1)=x\Gamma(x)\] この性質から,自然数 \(\small n\) に対して, \[\small \begin{align*} \Gamma(n+1)&=n\Gamma(n)\\ &=n(n-1)\Gamma(n-1)\\ &=n(n-1)\cdots 2\Gamma(1)\\ &=n! \end{align*}\] となり,ガンマ関数は自然数の階乗を実数にまで 拡張した関数であることが分かります. もともとは,階乗を複素数にまで拡張しようとして オイラーにより考案された関数のようです. 上記の性質は,部分積分を行うと簡単に確認できます. \[\small \begin{align*} \Gamma(x+1)&=\int_0^{\infty}t^{x}e^{-t}\,dt\\ &=\int_0^{\infty}t^x(-e^{-t})'\,dt\\ &=\big[-t^xe^{-t}\big]_0^{\infty}\\ &\qquad +x\int_0^{\infty}t^{x-1}e^{-t}\,dt\\ &=0+x\Gamma(x)=x\Gamma(x) \end{align*}\] さらに,\(\small \int_0^{\infty}e^{-x^2}\,dx=\frac{\sqrt{\pi}}{2}\) であることを利用すると, \(\small \Gamma\left(\frac12\right)=\sqrt{\pi}\) が得られます. 実際,\(\small x=\sqrt{t}\) と置換すると, \(\small 2dx=\frac{1}{\sqrt{t}}\,dt\) であることから 次のようになります. \[\small\begin{align*} \Gamma\left(\frac12\right) &=\int_0^{\infty}t^{-1/2}e^{-t}\,dt\\ &=\int_0^{\infty}e^{-x^2}\,2dx\\ &=\frac{\sqrt{\pi}}{2}\cdot 2=\sqrt{\pi} \end{align*}\] さらに,\(\small \Gamma(x+1)=x\Gamma(x)\) という関係を 利用すると,\(\small n\) が自然数のときは次のことも分かります. \[\small \begin{align*} &\Gamma\left(n+\frac12\right)\\ &=\left(n-\frac12\right)\Gamma\left(n-\frac12\right)\\ &=\left(n-\frac12\right)\left(n-\frac32\right)\Gamma\left(n-\frac32\right)\\ &=\left(n-\frac12\right)\left(n-\frac32\right)\cdots\frac12\Gamma\left(\frac12\right)\\ &=\frac{2n-1}{2}\cdot\frac{2n-3}{2}\cdots\frac12\sqrt{\pi} \end{align*}\] ここで,分子は 1 から \(\small 2n-1\) までの奇数の積になります. これを \(\small (2n-1)!!\) と表す場合があります. その記法を用いると,\(\small n\) が自然数のとき次の式が得られます. \[\small \Gamma\left(n+\frac12\right) =\frac{(2n-1)!!}{2^n}\sqrt{\pi}\] グラフも確認しておきましょう. 階乗の一般化ということで大きな値を取るので, 常用対数をとって \(\small \log_{10}\Gamma(x)\) の変化をみてみましょう. ガンマ関数は,いろいろな確率分布 を定義するときに頻出する重要な関数です. |
|
|
|
■デルタ関数 通常の関数の範疇には含まれないのですが, 衝撃を表すときに利用されるデルタ関数 \(\small \delta(x)\) も重要です. デルタ関数は, \[\small \delta(x)=\begin{cases} \infty & (x=0)\\ 0 & (x\ne 0)\end{cases}\] \[\small \int_{-\infty}^{\infty}\delta(x)\,dx=1\] という性質を持ち,任意の連続関数 \(\small f(x)\) に対して \[\small \displaystyle \int_{-\infty}^{\infty}f(x)\delta(x)\,dx=f(0)\] を満たします. デルタ関数は関数列 \(\small \left\{f_n(x)\right\}\) の 極限として \(\small \displaystyle \delta(x)=\lim_{n\to\infty}f_n(x)\) により定義されます.そのような関数列として, 次のような関数があります. \[\small \begin{align*} &\frac{\sin nx}{\pi x}\\ &\sqrt{\frac{n}{\pi}}e^{-nx^2},\quad \frac{n}{\sqrt{2\pi}}e^{-\frac{n^2x^2}{2}}\\ &\frac1{n\pi}\cdot\frac1{x^2+1/n^2}\\ &\begin{cases} n& \left(|x|\leq \frac1{2n}\right)\\ 0& \left(|x|>\frac1{2n}\right) \end{cases} \end{align*}\] 下図は \(\small \frac{\sin{nx}}{\pi x}\) の場合のグラフです. |
|
|
|
■高木関数 学校の教科書で出てくる関数は,大体の箇所では連続で微分可能です. そうではない点があったとしても,せいぜい数カ所ある程度の関数しか扱いませんが, 関数の中には,連続ではあるが至るところ微分可能ではない関数があります. 三角級数で表されるワイエルシュトラス関数が有名です. 次の式で定義されます. \[\small f(x)=\sum_{n=0}^{\infty}b^n\cos(a^n\pi x)\] ここで,\(\small a\) は奇数,\(\small b\) は \(\small 0\lt b\lt 1\) となる実数です.下図は,\(\small a=3, b=\frac12\) の場合に, \(\small n=1, n=5\) までの和のグラフです. 無限大まで加えたときの極限関数は, いたるところギザギザで微分可能ではありません (参照). これらの関数の詳細は,下記を参照してください. |
|
|
|
■q-対数関数とq-指数関数 これらの関数は,統計力学などの分野で必要になってきます. 要するに,通常の対数関数や指数関数をべき関数 \(\small x^a\) と結びつける関数です.
q-対数関数
q-指数関数
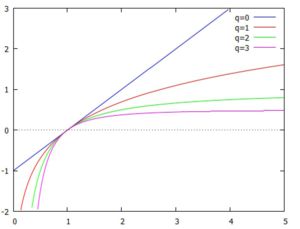
q-対数関数とq-指数関数のグラフ 下記はq-対数関数です.
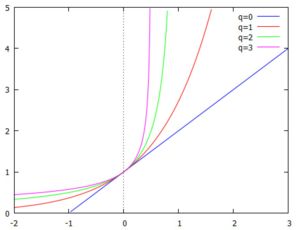
下記はq-指数関数です.
微分方程式のスケール不変性
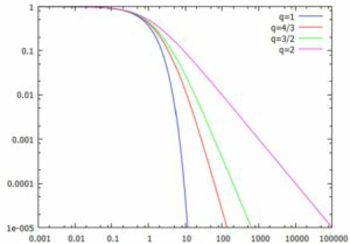
q-指数関数とべき関数 同様にすると,\(\small 0 < q < 1\) のときは, \(\small \exp_q(x)\propto x^{\frac1{1-q}}\) (増加関数)が得られます. 下記は,\(\small \exp_q(-x)\) を両対数グラフで示したものです.
両対数グラフで描画すると右下がりの直線状になる実データは,
この世界には山ほどあります[べき分布].
両対数グラフが直線状になるということは,
\[\small \log{y}=\log{C}-a\log{x}\]
という形になるので,\(\small y=Cx^{-a}\) の形です.
このときの「べき指数」は,概ね \(\small 2 < a < 3\) の値となることが
多いようです.q-指数関数でいえば,
\(\small 2 < \frac1{q-1} < 3\)の場合なので,\(\small \frac43 < q < \frac32\)
の場合になります.
具体的な値をみると,概ね \(\small x>30\) では値がほとんど一致します.
|
|
q-積とq-比 |
|
|
|