福井高専主催の第24回グラフ電卓研究会に参加して、
「べき乗則・相転移・浸透現象」について発表(紹介)してきました。
「べき分布」の重要性に遅まきながら気づいたのは数年前ですが、
そのことが数学教員にあまり認識されていないように思われたので、
自分なりにまとめたものをいろいろと発表してきました
(参照)。
「べき乗則」は確率分布ではなく、
2変量の間の関係がべき関数 \( \small y=kx^a\) で表わされる場合をいいます。
そのような関数で表わされる現象は、至るところで目にすることができます。
簡単な場合では反比例があります。ジップの法則も反比例の関係です。また、
ニュートンの万有引力の法則など、逆2乗に比例する場合もべき乗則の関係です。
特に、確率密度関数がべき関数で表わされるのがべき分布です。
その流れで調べていくと、「相転移」に突き当たります。
相転移は、ある箇所でその物質の性質が劇的に変ってしまう現象です。
相転移には不連続相転移と連続相転移の2種類あるといわれ、
水が氷になったり気体になったりするのは不連続相転移です。
連続相転移としては、たとえば磁石があります。
磁石を熱するとある温度で磁力を失います。
形は変化しなくても、中の性質が大きく変ってしまいます。
超伝導や超流動も、
温度を絶対温度に近い温度にまで下げていくと生じる連続相転移です。
連続相転移する物質は、他にも数え切れないくらいあるようです。
そして、そのような連続相転移の転移点の近傍では、
いろいろな量が転移点との距離に関してべき乗則で変化し、
発散するなどの特異な変化(臨界現象)を示します。
しかも、連続相転移するどの物質で調べても、
転移点の近傍ではべき乗則にしたがい
発散などの特異な変化をすることは同じであるようなのです。
たとえば、磁石(磁性体)の場合でいうと、転移点の温度を \(\small T_c\) として
\( \small t=(T-T_c)/T_c\) とすると、
比熱 \(\small C\) と自発磁化 \(\small m\) は
\( \small |t|\) のべき乗と比例関係にあり、
\(\small C\propto |t|^{-\alpha}\) \(\small (T>T_c)\)、
\(\small C\propto |t|^{-\alpha'}\) \(\small (T<T_c)\)、
\(\small m\propto |t|^{\beta}\) \(\small (T<T_c)\)
が成り立ち、\(\small \alpha=\alpha'\) が予想されています。
下図は、これらのグラフ(模式図)です。
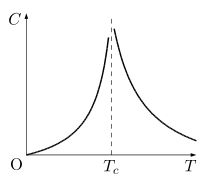

同様の比例関係が、磁石に関する他の量、
磁化率\(\small \chi\)、相関距離\(\small \xi\)、
相関関数\(\small G(r)\) などでも成り立ちます。
さらに、このような特異な変化を示すのは磁石の場合には限りません。
他の連続相転移する物質でも、比熱や自発磁化などに対応する量を考えると、
その転移点の近傍では同じような変化を示し、
その変化はやはりべき乗則で表わされるようなのです。
いろいろな量の変化は様々な関数で表わされますが、
相転移の転移点の近傍の変化は、
何故か、ことごとくべき関数で表わされるのです。
しかも、そのときの \(\small \alpha, \beta\) などのべき指数は、
同じような値をとる幾つかのクラスに分類できるようなのです。
臨界指数が同じような値を取るクラスはユニバーサルクラスと呼ばれています。
相転移という大きな変化を示す箇所の近傍の変化が
同じべき指数で表わされるということは、
そのクラスに属する物質は異なっても、
相転移が引き起こされる仕組みは同じであることが示唆されます。
たとえば、適当な温度で圧力を上げていくと液体と気体の間で相転移が生じますが、
この相転移も磁性体の相転移と同じユニバーサルクラス(イジングモデル)
に属するようです。
また、相転移の数学モデルとされる「パーコレーション」は、
別なユニバーサルクラスであるようです。
以上のことだけでも十分に驚きなのですが、
さらに深い仕組みが存在します。
相転移の転移点の近傍では、いろいろな量がべき乗則にしたがいます。
そのべき指数は臨界指数と呼ばれています。
異なるユニバーサルクラスでは臨界指数も異なりますが、
何と!、どのユニバーサルクラスでも、
臨界指数はある一定の関係式を満たしているようなのです。
たとえば、臨界指数をギリシア文字で表わすとき、
次のような関係式が成り立つようなのです。
\(\small 2-\alpha=\beta(\delta+1)=\gamma+2\beta\)
他にも多数の関係式が知られています。このような関係式は
スケーリング則と呼ばれています。
つまり、まとめると、次のようになっているようです。
- 2変量の関係がべき関数で表わされるとき、
「べき乗則」が成り立つという。
べき乗則で表わされる現象は、比例関係、逆2乗の関係、べき分布など多数に及ぶ。
- 物質の性質が劇的に変化する「相転移」の転移点の近傍では、
いろいろな量がべき乗則にしたがって変化し、発散などの特異な変化をする。
相転移する物質は多数あるが、どの相転移でも、転移点の近傍では
いろいろな量がべき乗則にしたがって変化している。
- そのときのべき指数(臨界指数)を調べると、同じような値をとるクラスに
分類することができる。そのクラスはユニバーサルクラスと呼ばれており、
同じクラスに属する物質の相転移は同じ仕組みで起きていると考えられる。
相転移の数学モデルとされる「パーコレーション」も、ユニバーサルクラスの
1つである。
- どのユニバーサルクラスでも、臨界指数は
\(\small 2-\alpha=\gamma+2\beta\) などの一定の関係式を満たしている。
スケーリング則という。
劇的に変化する連続相転移の転移点の近傍では、
どのような物質の相転移でも臨界指数の間に一定の関係式が成り立つというのは、
ただ事ではありません。その関係式は、
個々の物質の性質には依存しない性質です。
どのユニバーサルクラスでも同じ関係式が成り立つことから、
特定のユニバーサルクラスで臨界指数の間の関係を考察すれば、
そこでの結果は他のユニバーサルクラスにも転用可能と思われます。
特定のクラスとして、磁性体のモデルであるイジングモデルや
確率論のパーコレーションでは、数学を用いた理論的な考察が進められています。
特に、パーコレーションの研究では、2006年、2010年、2022年には
フィールズ賞が与えられており、この分野の研究の重要性が分かります。
ただし、物理・数学のいずれの方面から研究するにおいても、
それぞれの分野のかなり深い専門知識が必要であり、
簡単に手を出せる内容ではありません。そのこともあり、
この相転移・パーコレーションの問題は、
その分野にいない方には重要性があまり認識されていないのではないかと
思われます。
そのようなことも、今回の研究会で発表(紹介)しようと思った理由です。
(注) 以上のことは、関連するWebサイトや文献の「触り」の部分だけを
「眺めて」得られた認識です。chatGPTのお世話にもなりました。
私自身は、いずれの専門家でもありません。
誤りや認識違いがあるときは、ご指摘いただけると幸いです。


