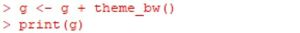|
�uR�v�̊�{����
|
�����ł́C���v�f�[�^����舵�����߂ɕK�v�ȁuR�v�̊�{����ɂ��āC
���Y�^�I�Ɏ��܂Ƃ߂܂����D
�uR�v�̃C���X�g�[�����܂ޑS�ʓI�ȉ���͑�������T�C�g���Q�Ƃ��Ă��������D
�g�p����̂�64bit�ł́uR�v(ver. 4.2.1)�ł��D
|
����{�I�ȉ��Z
�����ł́C�uR�v�Ɋւ����{�I�ȉ��Z�ɂ��Ă܂Ƃ߂܂����D
�ʏ�̎l�����Z�͉��L�̒ʂ�ł��D�~���� \(\small \pi\) �́upi�v�D
�������́usqrt()�v�ł��D�uR�v�ł̑���ɂ́u��-�v(���͔��p)���p�����邪�C
�u=�v�ł����܂��܂���D�l�I�ɂ́u��-�v���u=�v���悢�Ǝv���܂����C
�uR�v�̒ʏ�̏����ŏ����Ă����������悢�Ǝv���܂��D
�������C�u��-�v��p����Ƃ��́C
�s������}�C�i�X�L���Ƃ̍���������邽�ߑO��ɋ���ꂽ�����悢�ł��D
�����̃R�}���h�́u;�v�ŋ���ē��͂ł��܂��D
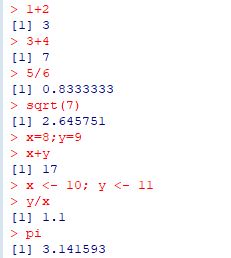
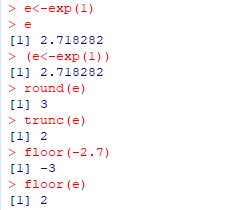
�l�C�s�A���́uexp(1)�v��K���ȕ����Ɋ��蓖�ĂĂ����Ƃ悢�ł��傤�D
�u( )�v�Ŋ���ƁC����Əo�͂������ɂȂ���܂��D
�l�̌ܓ��́uround�v�C��̂Ắutrunc�v�C
���̒l���Ȃ��ő�̐����́ufloor�v�ł��D
�x�N�g���́uc(a,b,c)�v�̂悤�Ȋ����œ��͂��܂��D
����́useq(start,end,step)�v�C
�A�����́urep(start:end)�v�ł���C��������x�N�g���Ƃ��Đ�������܂��D
1���݂̏ꍇ�́ustart:end�v�����ł����܂��܂���D

�x�N�g��������������C���ʕ������Ƃ����肷�邱�Ƃ��ł��܂��D
- �uappend(a,c)�v�ɂ��C�ua�v�̌�Ɂuc�v���lj�����܂��D
- �uappend(a,c,after=2)�v�ɂ��C�ua�v��2�Ԗڂ̗v�f�̌�Ɂuc�v���lj�����܂��D
- �uunion(b,c)�v�ɂ��C�ub�v�Ɓuc�v�̘a�W������������܂��D
- �uintersect(b,c)�v�ɂ��C�ub�v�Ɓuc�v�̋��ʕ�������������܂��D
- �usetdiff(a,c)�v�ɂ��C�ua�v����uc�v�̗v�f���������x�N�g������������܂��D
���}�́C��L�̑�����s�������̂ł��D
�Ȃ��C�v�f�������ɕ��בւ���ɂ́usort(v)�v�C
�~���́usort(v,decreasing=TRUE)�v�Ƃ��܂�(�}�͗�)�D

�����̃x�N�g�����܂Ƃ߂Ĉ�̃f�[�^�Ƃ��邱�Ƃ��ł��܂��D
�����������x�N�g�����ua�v�ub�v�Ƃ���Ƃ��C
�urbind(a,b)�v�ɂ��2�̍s(row)���܂Ƃ߂邱�Ƃ��ł��C
�ucbind(a,b)�v�ɂ��2�̍s���(column)�ɂ��Ă܂Ƃ߂邱�Ƃ��ł��܂��D

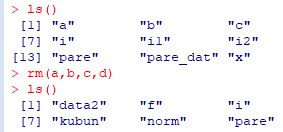
��`�����ϐ��̈ꗗ�́uls()�v�ŕ\������܂��D
�ϐ�����������ɂ́C�uremove(�ϐ�)�C�܂��́urm(�ϐ�)�v�Ƃ��܂��D
���}�́C�\����ʂ̍��������o�������̂ł��D
�ϐ��ua,b,c,d�v���������čēx�uls()�v�����s���܂����D
�ua,b,c,d�v�͕\������Ȃ��̂ō폜���ꂽ���Ƃ�������܂��D
|
|
����ʂ̑���
�uR�v�ł͖͋�������܂����C
�R�}���h�̒Ԃ�͈ꑱ���œ����K�v������܂��D
1�s�ɕ����̃R�}���h�������ɂ́u�G�v�ŋ��܂��D
�R�}���h���I�����Ȃ������ɁuEnter�v�������ƁC
�����̓��͂𑣂��u�{�v���\������܂��D
��ʂ�S����������ɂ́uctrl�v�{�ul�v(�G��)�C�܂��́C
�g�b�v���j���[�́u�ҏW�v����u�R���\�[����ʂ������v��I�����܂��D
�A���t�@�x�b�g�̑啶���Ə������͋�ʂ����̂ŁC
���͂ɂ͒��ӂ��K�v�ł��D

�R���\�[����ʂł�1�s�����͂��Ȃ���Ȃ炸�C�ς킵���Ƃ�������܂��D
���̂悤�ȂƂ��́C�R�}���h�̗�����X�N���v�g�ɏ����Ĉ�C�Ɏ��s������
���Ƃ��ł��܂��D
�V���ȃX�N���v�g�̍쐬�́C
�u�t�@�C���v����u�V�����X�N���v�g�v��I�����܂��D
�쐬�ς݂̃X�N���v�g��lj��E�C������̂ł���C
�u�X�N���v�g���J���v��I�����܂��D
�uR�G�f�B�^�[�v���J���̂ŁC�����ɃR�}���h���L�q���܂��D
���s�́C���s����X�N���v�g��I�����Đn�\���ɂ��Ă���
�uctrl�v�{�ur�v�������܂��D
���l�ɂ��āC�X�N���v�g�̈ꕔ���������s�����邱�Ƃ��ł��܂��D
���}�́C�E��������I�����āuctrl�v�{�ur�v����������Ԃł��D

�X�N���v�g���������t�@�C���́uR�v�̍�ƃt�H���_�[(working directory)
�ɕۑ����Ă����Ƃ悢�ł��傤�D
���݂ǂ̃t�H���_�[����ƃt�H���_�[�ɂȂ��Ă��邩�́ugetwd()�v�Ŋm�F�ł��܂��D
�ύX����Ƃ��́C�\�������t�H���_�[�̏����ɂȂ���āC
�usetwd("�t�H���_�[��")�v�Ŏw�肵�܂��D

�X�N���v�g�ɓ��{����g�p���邱�Ƃ��ł��܂��D
��ŐU��Ԃ�Ƃ��C�R�}���h�̂��낢��ȉ���������Ă����Ƃ悢�ł��傤�D
�s���Ɂu#�v�������ƁC���̍s�̓R�����g�s�ɂȂ�܂��D
|
|
�����̈���
�ʏ�̏��������g�p���邱�Ƃ��ł��܂��D
| sqrt | ������ |
| abs | ��Βl |
| exp | �w���� |
| log | ���R�ΐ� |
| log10 | ��p�ΐ� |
| sin | ������ |
| cos | �]���� |
| tan | ���ڊ� |
| floor | �K�E�X�L�� |
| ceiling | �V��� |
| trunc | ��̂� |
| round | �l�̌ܓ� |
�o�Ȑ����́usinh�v�ucosh�v�utanh�v�C
�t�O�p���́uasin�v�uacos�v�uatan�v�C������
�t�o�Ȑ����́uasinh�v�uacosh�v�uatanh�v�ł��D
�܂��C�K���}���́ugamma�v�ł��D
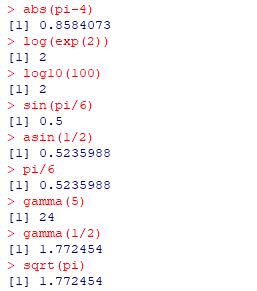
�V�����������ɂ́C
�u(����) ��- function(����){����)}�v(���͔��p)�Ƃ��������ɂȂ�܂��D
�Ō�̏������ʂ́ureturn(����)�v�Ƃ��܂��D
���Ƃ��C\(\small f(x)=2(x-2)^2+1\) ���ׂ��������Ē�`����
�ufun�v�Ƃ���ɂ́C���̂悤�ɂ��܂��D

��`��������Y��Ă��܂����Ƃ��́C���̒�`���ĕ\�������邱�Ƃ��ł��܂��D
�P�Ɋ�����ł����ނ����ł��D

|
|
����������E�J��Ԃ�
��������́uif-else�v�́C�uif (����) {����1} else {����2}�v�Ƃ��܂��D
���Ƃ��C
\[\small f(x)=
\begin{cases} -1 & (x\lt -1)\\ ~~0 & (-1\leq x\lt 1)\\ ~~1 & (1\leq x)\end{cases}\]
���`����ɂ́C���̂悤�ɂ��܂��D

�u��-�v�͑���L���Ȃ̂ŁC
���̑O��ɂ͋������悤�ɏK���Â��������悢�ł��傤�D
�܂��C�r���̃X�y���~�X�����������肷��̂ŁC�R���\�[����ʂł͂Ȃ��C
�X�N���v�g�ɏ����āuctrl�v�{�ur�v�ɂ����s���������悢�ł��傤�D
�v���O�������ŗp�����ϐ��̒l�͊O���ł͕ێ�����܂���D
�����L�q�̂Ƃ��̐^�U����̘_�����Z�q�Ƃ��āC
�u�����v�́u�����v�C�u�s��v�v�́u�I���v�C
�u���v�́u�����v�C�u�܂��́v�́u||�v�ł��D
�P�Ɍ��ʂ�Ԃ������̂Ƃ��́uifelse�v�Ƃ�������������܂��D
�uifelse(�����C�^�̂Ƃ��̌��ʁC�U�̂Ƃ��̌���)�v�Ƃ��܂��D
��������q�ɂ���C��L�Ɠ������͎��̂悤�ɋL�q���邱�Ƃ��ł��܂��D

�J��Ԃ������Ɂufor�v�����p�ł��܂��D������
�ufor (�ϐ� in �͈�) {����}�v�ł��D
���Ƃ��C�K��͎��̂悤�Ɍv�Z����܂��D
�C�ӂ̎��������ł��āC���̏ꍇ��0���C���̏ꍇ�͐��������܂ł̊K���
�l���Ԃ���܂��D�������C\(\small 0!=1\) �Ɋւ��鏈���͍s���Ă��Ȃ��̂ŁC
���p�I�ł͂���܂���D�ureturn( )�v�̈ʒu�ɒ��ӂ��K�v�ł��D

�������^�ł���ԂŌJ��Ԃ��ɂ́uwhile (����) {����}�v�Ƃ��܂��D
��L�̊K��́C���̂悤�ɂ���`�ł��܂��D

�����悤�ȌJ��Ԃ��Ɂurepeat�v�����p�ł��܂��D
�����́urepeat {����}�v�ł��D
������������ČJ��Ԃ����甲����ɂ́ubreak�v��u���܂��D
repeat�𗘗p����ƁC�K��͎��̂悤�ɂ���`�ł��܂��D
�v���O�����̊ȒP�̂��� \(\small 0!=1\) �Ɋւ��鏈���͍s����
���Ȃ��̂Ŏ��p�I�ȃv���O�����ł͂���܂���D
���p�ɕt���ɂ́C���̏ꍇ�̓��ʏ�����lj��L�q����悢�̂ł��D

|
|
���f�[�^�̌^
���͎����̑��ɕ��f���𗘗p���邱�Ƃ��ł��܂��D�����́u" "�v�ň͂��܂��D
�����P�� \(\small i\) �́u1i�v�Ƃ��ė��p�ł���̂ŁC
���f�� \(\small a+bi\) �́ua+b\(\small *\)1i�v�Ƃ��܂��D

���╶�������ɕ��ׂ����̂��x�N�g���ƌĂт܂��D
�R���}�ŋ���������x�N�g���Ƃ��Ĉ����ɂ́uc(a,b,c)�v�𗘗p���܂��D
�K����������������́ustep(start,end,by=step)�v�Ƃ��܂��D
���̂悤�ȃx�N�g���ɑ���l�����Z�́C�Ή�����v�f�ǂ����̉��Z�ɂȂ�܂��D
�Ȃ��C���}�� b/a �̌��ʂ̑O����������������̂ł��D
(�S����\������ƃX�}�z�ł̉�ʂ����Â炭�Ȃ�̂ŁD)

�P���Ɉ�萔�����������茸�����肷�鐔��͊ȒP�ɍ��܂����C
��ʓI�Ȑ���̓v���O������g��ō�邵���Ȃ��Ǝv���܂��D
���Ƃ��C�t�B�{�i�b�`����͎��̂悤�ɂȂ�܂��D

���낢��ȃx�N�g������ɂ܂Ƃ߂����̂̓��X�g�ƌĂ�܂��D
�����ł́C���l�C�����C�_���L���Ȃǂ��܂Ƃ߂Ĉ�̂���(�I�u�W�F�N�g)
�Ƃ��Ĉ������Ƃ��ł��܂��D�x�N�g������ׂčs��(matrix)�Ƃ��邱�Ƃ��ł��܂��D
�s��͍s�Ɨ���2�����ł����C
�z��(array)�𗘗p����Ƒ������̂��̂��l���邱�Ƃ��ł��܂��D����ɂ́C
�e��̗v�f���قȂ�^�̃f�[�^���������Ƃ��ł��܂����C
�����ł͓��v��͂ŕK�v�Ƃ���CSV�f�[�^�̎�舵���Ɍ��肵�čl���܂��D
|
|
���f�[�^�̓��o��
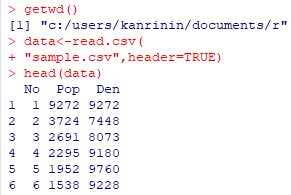
���v�f�[�^�͗Ƃɂ݂܂��D1�s�ڂɗ�̖��O��u�����Ƃ��ł��܂��D
�R���}���̃f�[�^�́ucsv�v�ł��D
���Ƃ��C
���L�̃f�[�^(sample.csv)��ǂݍ��ނ��Ƃɂ��܂��D

csv�t�@�C����ǂݍ��ނɂ�
�uread.csv("filename", header=TRUE)�v
�܂��́uread.table("filename",header=TRUE,
sep=",")�v�Ƃ��܂��D
1�s�ڂɗ��Ȃ��Ƃ��́uheader=FALSE�v�Ƃ��܂��D
���̏ꍇ�́C�e��ɁuV1, V2, V3�v�Ȃǂ̗������I�Ɋ���U���܂��D
�uread.table�v�𗘗p����ƁC
��^�u�ȂǑ��l�ȋ��L�������p�ł��C
���낢��ȓǂݎ����������邱�Ƃ��ł��܂����C
�����ł͏ڍׂ͏ȗ����܂��D
�f�[�^�����udata�v�Ƃ���Ƃ��C
�uhead(data)�v�Ƃ���Əo������6�s���C
�utail(data)�v�Ƃ���ƍŌ��6�s���C
�udata�v�Ɠ��͂���ƑS�f�[�^���\������܂��D
�f�[�^���������Ƃ��͕\���̂������ɂ͒��ӂ���K�v������܂��D
���ɕK�v���Ȃ�����Chead�ł̕\�����K���Â��������悢��������܂���D
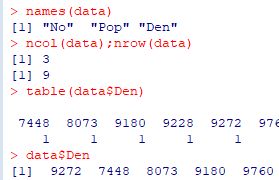
�ǂݍ��f�[�^�̗�����\��������ɂ́unames( )�v�C
�́uncol( )�v�C�s���́unrow( )�v�Ƃ��܂��D
�s���́C������Ƃ��͎��f�[�^�̗ɂȂ�܂��D
�f�[�^�̗���w�肷��ɂ́udataname���v(���͔��p)�Ƃ��܂��D
���̃f�[�^(data)��3��ڂ́uDen�v�Ȃ̂Łudata��Den�v�Ƃ��܂��D
���t����Ă��Ȃ��Ƃ��́udata��V3�v�Ƃ��܂��D
�utable(dataname����)�v�Ƃ���ƁC
���̃f�[�^�����������ɕ��בւ����āC
�����l�����x�����\������܂��D
���U�I�Ȓl�̏ꍇ�͓x�����z�\���\������邱�ƂɂȂ�܂��D
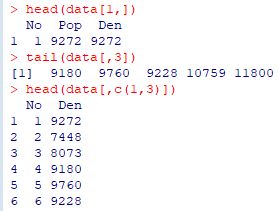
i�s�ڂ�j��ڂ�\��������ɂ́udata[i,]�v��udata[,j]�v�Ƃ��܂��D
i���j���\��������ɂ́udata[,c(i,j)]�v�Ƃ��܂��D
�������C�uhead�v��utail�v�ň͂��ĕ\�������������悢�ł��傤�B
�Ȃ��C���}�ł�(�X�}�z�\���ł̌��₷���̂���)��ʉE���̈ꕔ���ȗ����܂����D
|
|
|
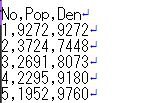
�t�@�C�����R���}���̃t�@�C��(csv)�ŕۑ�����ɂ́C
�uwrite.csv(�f�[�^��, "filename")�v�Ƃ��܂��D
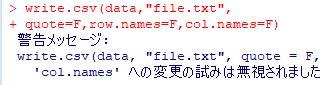
���}�́C�uwrite.csv(data,"file.txt")�v�Ƃ����ꍇ�ł��D
���5�s���������܂����D

���ꂩ�番����悤�ɁC�P���ɕۑ�����ƁC
��s�������p���ň͂�ŕۑ�����܂��D
���p�������Ȃ��悤�ɂ���ɂ́uquote=F�v�C
�����čs�����ȗ�����ɂ́urow.names=F�v��lj��w�肵�܂��D
�������C���ȗ�����ucol.names=F�v�Ƃ����w��́C
�uwrite.csv�v�ł͖�������ė������o�͂���܂��D
����́uR�v�̎d�l�̂悤�ł����C
�uwrite.csv�v�Ƃ����R�}���h���̂����������āucol.names=F�v��
�L���ɂ��邱�Ƃ��ł���悤�ł�(
�Q��)�D
���̗��ȗ����ĒP�Ȃ�f�[�^����ۑ�����ɂ�
�uwrite.table�v�𗘗p���܂��D
���̏ꍇ�́C�R���}���ł��邱�Ƃ��w�肷�邽�߂Ɂusep=","�v��
�lj��w�肷��K�v������܂��D

|
|
����f�[�^�̏���
|
�T���v���f�[�^
���v�\�t�g�ł���̂ŁC
�ǂݍ��f�[�^�ɂ��낢��ȏ������s�����Ƃ��ł��܂��D
�����ł́C
�T���v���f�[�^�Ƃ��āusample2.csv�v���g�p���܂��D
���̃f�[�^�́CMaxima�𗘗p����50�̗��������������̂ŁC
�e��̓��e�͎��̒ʂ�ł��D
| 1��ځF | 1�`6�̐�������Ȃ闐���D |
| 2��ځF | ���zBin(10,1/6)�ɂ�闐���D |
| 3��ځF | ���K���zN(50,10)�ɂ�闐���D |
| 4��ځF | �p���[�g���zPare(1,1)�ɂ�闐���D |
| 5��ځF | ������{A,B,C,D}�̃����_�����o�D |
�Ȃ��C���K���z�͎l�̌ܓ����Đ����Ƃ��܂����D
�p���[�g���z�� \(\small 1/x^2~(x\geq 1)\) �ɂ������������ŁC
������1�ʂ܂ł̒l�Ƃ��܂����D
���}�́C���̃t�@�C����ǂݍ���Ő擪��6�s���o�͂��������̂ł��D
1�s�ڂɗ�����Ƃ��́C
�uheader�v�ɂ��^�U�̎w������Ȃ��Ă����Ɠǂݍ��܂�܂��D

|
��f�[�^�̑���
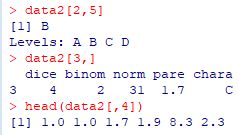
���ꂼ��̃f�[�^�͗�f�[�^�Ȃ̂Łudata2�v�͍s��`���̃f�[�^�ł��D
���������āC\(\small (i, j)\) ������ data2[i,j] �ɂ��Q�Ƃ��邱�Ƃ��ł��܂��D
��i�s�� data2[i, ]�C��j��� data2[ ,j] �ł��D
�s�͗̉��ɂ���f�[�^�s�ł��D
���}�ł́C(2,5)�����C3�s�ځC������4��ڂ��o�͂���Ă��܂��D
1���̏ꍇ�́C�����т̃x�N�g���Ƃ��ďo�͂���܂��D
����̗�(���Ƃ��C3��ڂ�4���)�����o���ɂ́C
��̉ӏ��� c(3,4) ���w�肵�܂��D
�t�ɁC����̗������ɂ� -c(3,4)���w�肵�܂��D
�s�ɂ��Ă����l�̎w�肪�ł��܂�(�}�͗�)�D
��������C
�uhead�v�����Ȃ���50�s�S�����\������܂��D
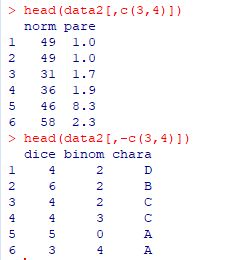
���̎w��ŁCc(3,4) �����Ƃ��� c(4,3) �ɂ���ƁC
4��ڂ��ŏ��ɕ\������܂��D���}�ł́C4��ڂ�2��ڂ���肾���Ă��܂��D

����̗��1�����o���ƃx�N�g���Ƃ��ĕ\������܂����C
��Ƃ��Ď��o���ɂ́udrop=F�v��lj��w�肵�܂��D
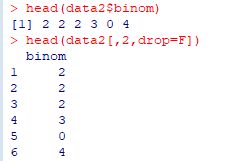
���}�ł�2��ڂ� data2$binom �����o���Ă��܂��D
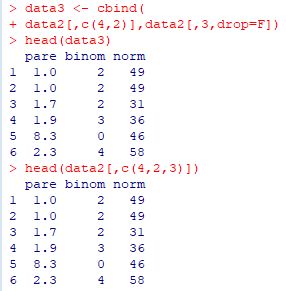
�ȏ�̏�����g�ݍ��킹��ƁC����̗�f�[�^��g�ݍ��킹��
�V�����f�[�^�s������邱�Ƃ��ł��܂��D
������s�����́ucbind�v�ł��D
���}�ł́C4�s�ځC2�s�ځC������3�s�ڂ���Ȃ�f�[�^�s��� data3 �Ƃ���
��`�������̂ł��D
�������C����� data2 �̗�����ւ��Ă��邾���Ȃ̂ŁC
���ۂɂ́Cdata2[,c(4,2,3)] �����ōς݂܂��D
��ł͂Ȃ��s�x�N�g������������ɂ́urbind�v�𗘗p���܂�
�D
|
|
��{���v��
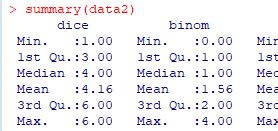
�f�[�^�̓��v�I�����́usuumary�v�ŁC
���ׂĂ̗�ɂ��Ĉ�ʂ�̒l���o�͂���܂��D
���}�́C3��ڂ̓r���܂ł��o�������̂ł��D
�e��ɂ��āC
�ŏ��l�C��1�l���ʐ��C���f�B�A���C���ρC��3�l���ʐ��C�����čő�l�̏���
�\������܂��D
���w�肷��ƁC�w�肵����ɂ��Ă̌��ʂ������܂��D

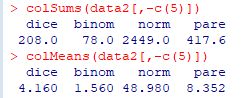
���l�f�[�^�̏ꍇ�C2��ȏ�̑��a�� colSums�C���ς� colMeans
�ɂ�苁�߂邱�Ƃ��ł��܂��D�s�ɂ��Ă� rowSums, rowMeans �ł��D
���}�ł́C�����f�[�^�ł���5������������a�╽�ς����߂Ă��܂��D
���̏����ŕ��U�����߂���͂Ȃ��̂ŁC�K�v�ł���Ύ����ō�邱�ƂɂȂ�܂��D
�ʂ̓��v�ʂƂ��āC���a�́usum�v�C���ς́umean�v�C
�s�Ε��U�́uvar�v�C�W�����́usd�v�C
�ŏ��l�́umin�v�C�ő�l�́umax�v�C���ʐ��́uquantile�v�C
�͈͂́urange�v�C�����ă��f�B�A���́umedian�v�ł��D
�������CcolSums, colMeans �������ƁC
�W���I�ȗ��p�ł͕�����̌��ʂ���x�ɓ��邱�Ƃ͂ł��܂���D
���̂悤�ȏ������K�v�ȂƂ��́C
������o�͂�������������ō�邱�ƂɂȂ�܂��D
�܂��́C���̂悤�Ȋ����o�^����Ă���p�b�P�[�W
(���Ƃ��ufBasics�v)��
�ǂݍ��ޕK�v������܂��D
�܂��C�s�Ε��U�͕W�{���U�ł͂Ȃ��̂Œ��ӂ��K�v�ł��D
�W�{���U���K�v�ȂƂ��͕s�Ε��U�������� \(\small (n-1)/n\) �{���܂��D
���ʐ��́��_�̒l���\������܂��D���}�ł́C��3��ɑ���
���ρC���U�C������80���_�����߂Ă��܂��D

|
|
�x�����z�E�N���X�\
�x�����z�\�́C�utable�v�𗘗p����ƊȒP�ɋ��߂邱�Ƃ��ł��܂��D
���}�́C���U�f�[�^�ł����2��̏ꍇ�ł��D
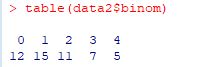
��1���1�`6�̐����������_���ɏo�͂������̂ł��D
���̃f�[�^�ł́u6�v�����ďo�͂���Ă��܂����C
������Ȃ��5��Ƒ�1��Ƃ̃N���X�\���ȒP�ɏo�͂���܂��D
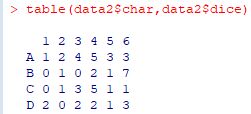
��3��͘A�����z�ł��鐳�K���zN(50,10)�̃f�[�^�ł��D
�����₷���悤�Ɏl�̌ܓ����Đ����l�ɂ��Ă��܂����C
���̃f�[�^���K���ɕ����ēx�����z���쐬���邱�Ƃ��e�Ղł��D
�X�̃f�[�^���ǂ̊K���ɑ����邩�ŋ敪�����邽�߂̊��Ƃ��āucut�v������܂��D
�ucut(�f�[�^, �敪�_�̃x�N�g��)�v�Ƃ���ƁC
�X�̃f�[�^���Y������K�� (a,b] �Œu���������܂��D
���L�ł́C�ŏ��� data2��norm �̏o������6�s���m�F���C
���Ɂuseq�v�𗘗p����[10,90] �͈̔͂�10���݂ɕ����C
���̋敪�_���܂Ƃ߂��x�N�g�����ukubunten�v�Ƃ��Ă��܂��D
�����āC���̋敪�_�� data2��norm �̃f�[�^���敪�����āunorm_kubun�v�Ƃ��܂��D
�X�̃f�[�^���C���̒l��������K�� (a,b] �Œu���������Ă��܂��D
���̊K���f�[�^�ɑ��āutable�v�𗘗p����ƁC
�K�����Ƃ̓x�����z�\�������邱�ƂɂȂ�܂��D
���}�ł͉E�����͏ȗ�����Ă��܂��D

|
�f�[�^�̕W����
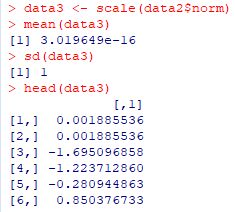
�f�[�^��W����������́uscale�v�ł��D
�f�[�^���w�肷��ƁC((�f�[�^)-(����))/(�W����) �ɂ��C
���ς�0, �W������1�̃f�[�^��ɕϊ�����܂��D
|
|
���f�[�^�̃O���t��
1�ϗʂ̃f�[�^
�f�[�^ x �́C�uplot(x)�v�ɂ��O���t�����邱�Ƃ��ł��܂��D
���̂Ƃ��C�f�[�^�̃^�C�v�ɂ�莟�̂悤�ȃO���t�ɂȂ�܂��D
- x ���x�N�g���^�ŁC�v�f�����ׂĎ����̂Ƃ��́C
�����͉��Ԗڂ���\�����R���C�c���ɂ͗v�f�̒l���v���b�g����܂��D
- x �̗v�f�����f���̂Ƃ��́C�����������C�c���������Ƃ���v���b�g�ɂȂ�܂��D
- x ��2��̍s��^�f�[�^�̂Ƃ��́C1��ڂ������C2��ڂ��c���Ƃ���
�v���b�g����܂��D
���}�́Cdata2��norm �̃f�[�^���v���b�g�������̂ł��D
�P�Ɂuplot�v����ƁC�f�[�^������ł��鏇�ɓ_���ۈ�Ńv���b�g����܂��D
�͈͎͂����Őݒ肳��܂��D
�z�u����_�̎�ނ́u�_�E����E�F�v���Q�Ƃ̂��ƁD

�����͈̔͂� xlim=c(start,end)�C�c���͈̔͂� ylim=c(start,end) �̌`��
�w�肷�邱�Ƃ��ł��܂��D
�ۈ����Ōq���ɂ́utype="o"�v���w�肵�܂��D
���낢��Ȍ��ѕ��́u�_�E����E�F�v���Q�Ƃ̂��ƁD
�ΐ����Ƃ���ɂ́C�ulog="x"�v�ulog="y"�v�ulog="xy"�v�Ȃǂ�lj��w�肵�܂��D
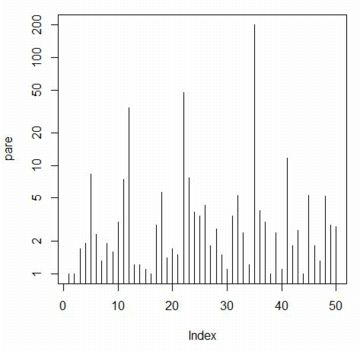
���}�́Cdata2��pare (���͔��p) ��
�c����ΐ����ɂƂ�C����ɉ����܂ł̐��������������̂ł��D
�����́C�utype="h"�v���w�肵�܂��D
|
1�ϐ����̃O���t
�uR�v�ɓo�^����Ă���W�����́C
���̖��̂��w�肷�邾���ŃO���t��`�悷�邱�Ƃ��ł��܂��D
���Ƃ��C������ \(\small \sin(x)\) �̃O���t��`���ɂ́C
���̖��̂Ɣ͈͂��w�肷�邾���ł��D
�������C�usin(x)�v�Ƃ���ƃG���[�ƂȂ�̂Œ��ӂ��K�v�ł��D
�͈͂́uxlim=c(-pi,pi)�v�Ƃ��Ďw�肷�邱�Ƃ��ł��܂��D
\(\small y\)���͈̔͂��w�肷��ꍇ�́C�uylim�v�ɂ��ē��l�ɂ��܂��D
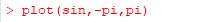
\(\small f(x)\) �̃O���t��`���ɂ́C���̊����`������ŁC
�uf�v�����̖��̂Ƃ��Ďg�p���܂��D�ux^3-3\(\small *\)x�v �̂悤��
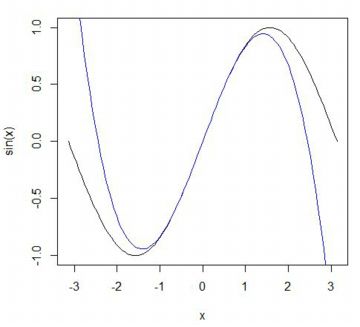
���̎��ړ��͂���ɂ́ucurve�v�𗘗p���܂��D
���Ƃ��C\(\small f(x)=x^3-3x\) �ł���Ύ��̂悤�ɂ��܂��D

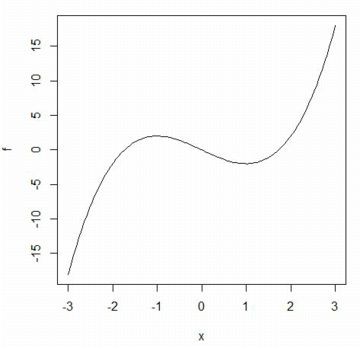
�O���t���d�˕`������ɂ́uadd=TRUE�v(�܂��́uadd=T�v)���w�肵�܂��D
����(line type)�́ulty�v�Ŏw��ł��܂��D�����́ulty=1�v�ł���C
�f�t�H���g�ł͏ȗ�����܂��D�T�C���J�[�u�������ŁC
�R�T�C���J�[�u��j��(lty=2)�ŕ`�悷��ɂ͎��̂悤�ɂ��܂��D
����ׂ̍����w��́u�_�E����E�F�v���Q�Ƃ̂��ƁD

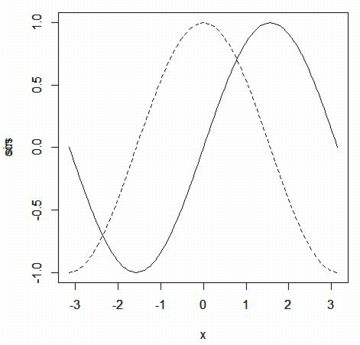
�O���t���d�˂�ƁC\(\small y\) ���̃��x�����d�Ȃ��Ă��܂��܂��D
���̃��x���́C�����́uxlab�v, �c���́uylab�v�ɂ��w��ł��܂��D
���Ƃ��C��L�̃O���t�ŃR�T�C���J�[�u�̃��x����\�����Ȃ��悤��
����ɂ́C�R�T�C���J�[�u�̉ӏ��Łuylab=""�v���w�肵�܂�(�}�͗�)�D
�uR�v�ł́C�O���t�`��Ɋւ��鑽���̊��𗘗p���邱�Ƃ��ł��܂��D
�uplot�v�̑��Ɂucurve�v������܂��D�����́uplot�v�Ɠ��l��
�ucurve(���C���[�C�E�[)�v�ł����C���̎��ړ��͂��邱�Ƃ��ł��܂��D
���}�́C2�̊� \(\small \sin(x), x-\frac{x^3}{6}\) ���d�˕`�����Ă��܂��D
�O���t���d�˕`������ɂ́uadd=TRUE�v�Ƃ��܂��D
�P�Ɂuadd=T�v�����ł����܂��܂���D
�Ȑ��̐F�́ucol�v�Ŏw�肵�܂��D���}�ł�2�Ԗڂ̋Ȑ����(blue)�Ƃ��܂����D
�F�ׂ̍����w��́u�_�E����E�F�v���Q�Ƃ̂��ƁD

|
|
�_�E����E�����E�F��
���U�f�[�^�̏ꍇ�ɔz�u����_�́C�f�t�H���g�ł͊ۈ�ł��D
�z�u�����́upch�v�Ŏw�肷�邱�Ƃ��ł��C�f�t�H���g�̊ۈ�́upch=1�v�ł��D
��Ɏg�p����Ǝv����L���Ƃ��ĉ��L�̂悤�Ȃ��̂�����܂��D
�Ȃ��C7�`14�ɊԂɂ�0�`6�̋L����g�ݍ��킹���L�����o�^����Ă��܂��D
| pch | �L�� |
pch | �L�� |
pch | �L�� |
| 0 | �� |
4 | �~ |
16 | �� |
| 1 | �� |
5 | �� |
17 | �� |
| 2 | �� |
6 | �� |
18 | �� |
| 3 | �{ |
15 | �� |
�f�t�H���g�ł͓_���z�u����邾���ł��D�_�ǂ�������Ō��Ԃ��ǂ�����
�utype�v�Ŏw�肵�܂��D�f�t�H���g�͓_��u�������Ȃ̂Łutype="p"�v
���w�肵�����ƂɂȂ�܂��D
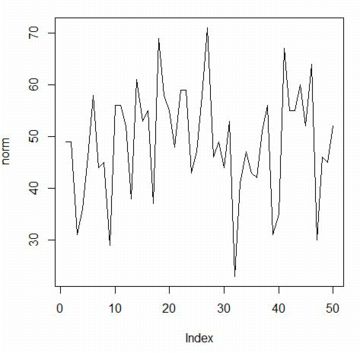
��(line)�Ō��Ԃɂ́uplot(norm,type="l")�v(�G��)�Ƃ��܂��D
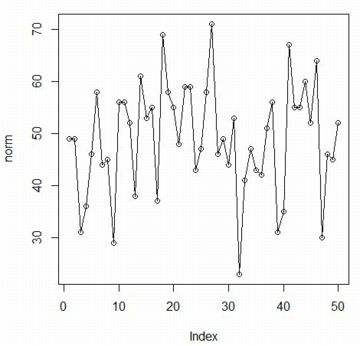
���u���Đ��Ō��Ԃɂ́utype="o"�v(�I�[)�C
�����������ɂ́utype="h"�v�Ƃ��܂��D
���}�́C���̏��ɕ\�������O���t�ł��D
type="l"
type="o"
type="h"

�f�t�H���g�ł͎����ŕ`�悳��܂��D
����(line type)�́ulty�v�Ŏw�肵�C�f�t�H���g�̎���(solid)�́ulty=1�v�ł��D
�ulty�v�̒l�ɉ����āC�j��(dashed,lty=2)�C�_��(dotted,lty=3)�C
����(dotdash,lty=4)�C���j��(longdash,lty5)�Ȃǂŕ`�悳��܂��D
�ԍ��̑��ɁC�_���ł���ulty="dotted"�v�̂悤�Ɏw�肷�邱�Ƃ��ł��܂��D

���̑����́ulwd�v�Ŏw�肵�܂��D�f�t�H���g�̒l�́ulwd=1�v�ł��D
���}�́C�utype="o"�v���w�肵�đ����ulwd=3�v�ŕ`�悵�܂����D
�Ȑ��̐F�́ucol�v�Ŏw�肵�܂��D��̓I�ȐF�Ƃ��ẮC
��(1, black)�C��(2, red)�A��(3,green)�C��(4, blue)�C
���F(5, cyan)�C��(6, purple)�C��(7, yellow)�C�D(8,gray)�����p�ł��܂��D
�ucol="red"�v�̂悤�ɐF�̖��O���w�肷�邱�Ƃ��ł��܂�(���})�D
�������C���ۂɂ͂����Ƒ����̐F���o�^�ς݂ł��D
�ǂ̂悤�ȐF�����邩�́ucolors()�v�����s���Ă݂�Ƃ悢�ł��傤�D
657�F�̖��O���\������܂��D�S���̐F�̕\����]�܂Ȃ��Ƃ��́C
�uhead(colors())�v���utail(colors())�v�Ƃ��čŏ��ƍŌゾ���\�������܂��D
���}�́C�o�����ƍŌ�̕����̍������ł��D
�Ȃ��C16�i��rgb�R�[�h���w�肵�āucol=rgb(��,��,��)�v�̂悤��
�w������邱�Ƃ��ł��܂��D


�_�ɔz�u����L���C����C�����C�����ĐF�̎w��́ucurve�v�ł����p�ł��܂��D
�͈͎w��ł́uxlim=c(statr,end)�v�uylim=c(start,end)�v�����p�ł��C
���̖ڐ�����ׂ����w�肷�邱�Ƃ��ł��܂�
(�Q��)�D
|
|
�q�X�g�O����
�f�[�^�̓��������ނɂ́C
��\�l�����߂邾���ł͂Ȃ��O���t������̂���Ԃł��D
�uR�v�ł̓q�X�g�O�������ȒP�ɕ`�悷�邱�Ƃ��ł��C
�uhist(�f�[�^)�v�Ƃ��邾���ł��D
���̃f�[�^�̓x�N�g���^�̃f�[�^�ł���K�v������܂��D
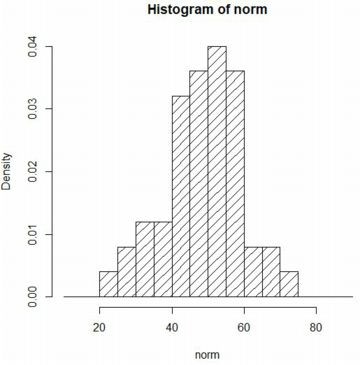
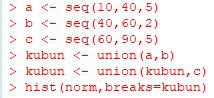
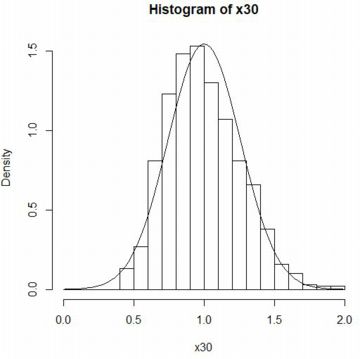
�ȉ��́C��f�[�^�ł��� data2��norm ���unorm�v�Ƃ���
�x�N�g���^�ɒu�������āuhist(norm)�v�Ƃ����Ƃ��̐}�ł��D
�f�t�H���g�ł͏c���͓x��(frequency)�ŕ\������C
�ufreq=TRUE�v���ȗ�����Ă��܂��D
�X�̊K���� \(\small (a,b]\) �Ƃ����E����Ԃł���C
�uright=TRUE�v���ȗ�����Ă��܂��D\(\small [a,b)\) �ōl�������Ƃ���
�uright=FALSE�v�Ƃ��܂��D

�K���̐� (k) �̓X�^�[�W�F�X�̌��� \(\small k\approx 1+\log_2(�f�[�^����)\)
�ɂ�茈�߂��C����ɂ��K������K�������ݒ肳��܂��D
���̊K�������́ubreaks�v�ɂ��ݒ肵�܂��D
�f�t�H���g�ł́ubreaks="Sturges"�v���w�肳��Ă��܂��D
���̕��������߂�A���S���Y���Ƃ��āC
���ɁuScott�v�uFD�v�uFreedman-Diaconis�v�Ƃ������̂�����悤�ł��D
�K�������ubreaks=20�v�̂悤�ɒ��ڂ��邱�Ƃ��ł��܂��D
�����_�������Ō��߂�ɂ́C
���̕����_���߂�x�N�g�����w�肵�܂��D
�unorm�v��N(50,10)�ł̗����Ȃ̂ŁC
���Ƃ���� [10,90] ��5���݂̊K���Ƃ���ɂ́C
�敪�_�̃x�N�g���Ƃ��āuseq(10,90,5)�v���w�肵�܂��D
���}�́C���Ɂufreq=FALSE�v(�P�Ɂufreq=F�v�ł��悢)�Ƃ��ďc�����m�����x�Ƃ��C
�udensity=10�v�ɂ��ΐ��������Ă��܂��D
�ΐ��̖��x�́C���̐��̑����Œ������܂��D
�F�̎w��́ucol�v�ɂ��s���܂�(�}�͗�)�D

�K���̋敪�_�́ubreaks�v�ɗ^����x�N�g���Ŏw��ł��܂��D
���̊Ԋu�͕K�������ϓ��ł���K�v�͂���܂���D
���Ƃ��C[10,40] �� [60,90] ��5���݂ɂ���
[50,60] ��2���݂ɂ���ɂ́C�敪�_���߂�x�N�g�������̂悤�ɒ�߂܂��D
���}�̃x�N�g���ua�v�ub�v�uc�v�́C���ꂼ��[�_�̒l���d������̂ŁC
�a�W���uunion�v������Ă��܂��D
�uhist�v�Łufreq=FALSE�v�̎w������Ă��Ȃ��̂ɁC
�Ȃ����c���͊m�����x�ŕ\������܂����D
�K�������ψ�łȂ��Ƃ��́C�c���͎����I�Ɋm�����x�ɂȂ�悤�ł��D
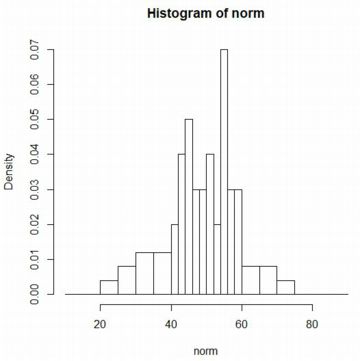
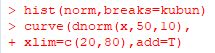
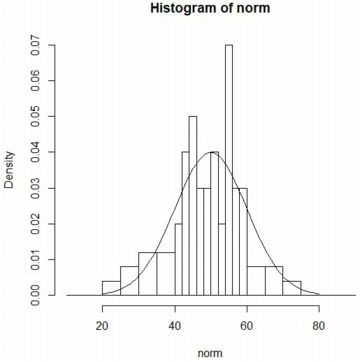
����Ɋm�����x�����d�ˍ��킹��ɂ́ucurve�v�𗘗p���܂��D
���K���zN(50,10)�̊m�����x���́udnorm(x,50,10)�v�ł��D
�����͈̔͂����킹�āC�d�˕`�����邽�߂Ɂuadd=T�v���w�肵�܂��D
|
|
|
�ȏ�́C���K���z�����Ƃɂ��܂������C
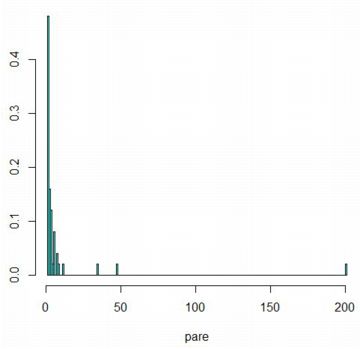
���Ƀx�L���z(�p���[�g���z)�̃f�[�^��p���ăq�X�g�O������`�悵�Ă݂܂��傤�D
�x�L���z�̊m�����x���� \(\small f(x)=ab^{a}/x^{a+1}~(x\geq b)\)
�ɂ���`����܂��D�udata2��pare�v�́C\(\small a=1, b=1\) �̏ꍇ��
�x�L���z�ɂ�����������1000����Ȃ��x�N�g���ł��D


���̏ꍇ�̃x�L���z�͕��ς����U�����݂��Ȃ��̂ŁC
������������ƁC���܁C�Ƃ�ł��Ȃ��傫�Ȓl���������܂��D
���}�ł́C�ő�l�ׂāC���̉ӏ��܂ł�1���݂ɂ��܂����D
�啔����20���x�܂ł̒l�ł����C
�傫���͂��ꂽ�l�������������Ă��邱�Ƃ�������܂��D
�Ȃ��C�^�U�l�́uTRUE�v�uFALSE�v�́C�P�� T, F �����ł����܂��܂���D

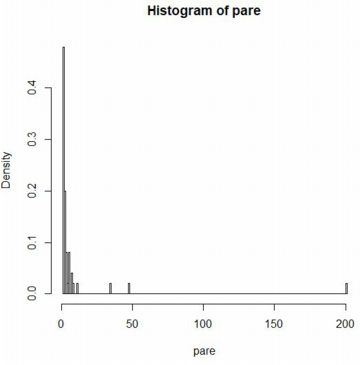
20���x�܂ł̕������ڂ������邽�߁C�͈͂����肵�܂��D
���}�ł� [1,15] �͈̔͂�\�����܂����D

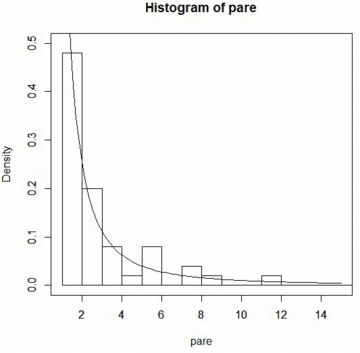
���}�́C���̃O���t�Ɋm�����x���ł��� \(\small 1/x^2\) ��
�uadd=TRUE�v�ɂ��d�˕`���������̂ł��D
���̃��x�����d�Ȃ�Ȃ��悤�ɁC���x���ł̃��x���̏o�͂�}�����܂����D

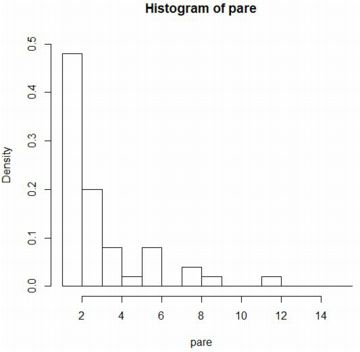
�Ȃ��C���̃x�L���z�̂悤�ɁC�����L�����z�̃q�X�g�O������`�悷��ɂ�
�uhist�v�͂�����Ǝg���ɂ����Ƃ��낪����܂��D
�ő�l���ׂ�ڂ��ɑ傫�Ȓl�ƂȂ�̂ŁC�W���̎d�l�ł͍ŏ��Ɏ������悤��
�O���t�ɂȂ�܂�(�Q��1)�D
�ׂ�������ɂ͍ő�l�ׂĕ��������w�肷�邱�ƂɂȂ�܂����C
�S�̑��͂�͂蕪����₷���}�ł͂���܂���(�Q��2)�D
���̂悤�ȃq�X�g�O�����������Ƃ��́utruehist�v�𗘗p���܂��D
���̊��́C�p�b�P�[�W�uMASS�v(Modern Applied Statistics with S)
�Ɋ܂܂�Ă���̂ŁC�܂������ǂݍ��܂��܂��D
�uhelp(truehist)�v�Ƃ���Ə������\������܂��D
�uhist�v�ƈႢ�C�ő�l���w�肷�邱�ƂȂ����ݕ�(h)���w�肷�邾���ł��D
�܂��C�f�t�H���g�ŏc���͊m�����x�ŕ\������܂��D
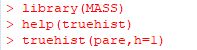
�ubreaks�v���g�p�ł��܂����C�uh�v�Œ��ڍ��ݕ����w�肷������ȒP�ł��D
�x����\�����������Ƃ��́uprob=F�v�Ƃ��܂��D
�uhist�v�Ɠ��l�ɁC�uxlim�v�uylim�v�ucol�v�uxlab�v�uylab�v���g�p�ł��܂��D
�f�t�H���g�ł́ucol="cyan"�v�Ƃ��ĕ\������܂��D
���}�́C0.5���݂ɂ��ĕ\���͈͂� [0, 15] �Ƃ����ꍇ�ł��D
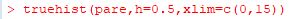
���Ȃ��C2�̃q�X�g�O�������d�ˍ��킹��ɂ�
�u�����v���C
�܂���ŕ`�悷��ɂ́u�q�X�g�O����(2)�v���Q�Ƃ��ꂽ���D
|
|
|
�uR�v�̉��p����
|
�����ł́C�m�����z���������߂ɕK�v�ȁuR�v�̉��p�I����ɂ��Ď��܂Ƃ߂܂����D
�S�ʓI�Ȑ��������̉���T�C�g���Q�Ƃ��Ă��������D
|
���낢��Ȋm�����z
�uR�v�͓��v�����\�t�g�Ȃ̂ŁC���낢��Ȋm�����z�ɂ��āC
���̊m�����x��(pdf)�C�ݐϕ��z��(cdf)�C���ʊ�(quantile)�C
�����ė�������(random)�Ɋւ�������p�ӂ���Ă��܂��D
�m�����x���� \(\small f(x)\) �Ƃ���Ƃ�
�ݐϕ��z���� \(\small F(x)={\rm P}(X\leq x)=\int_{-\infty}^{x}f(x)\,dx\)
�ł��D��ߕ����� \(\small 0\leq F(x)\leq 1\) �ł��D
�܂��C���ʊ��͗ݐϕ��z���̋t���ł���C
\(\small F(x)=q\) �Ƃ����� \(\small x=F^{-1}(q)\) �����ʊ��ł���C
\(\small {\rm P}(X\leq x)=q\) �����藧���܂��D
�uR�v�ŗ��p�ł����Ȋm�����z�ƁuR�v�ł̖��͎̂��̒ʂ�ł��D
���ɂ�����܂����C�l�I�Ɏg�������ɂȂ����̂͏ȗ����܂����D
| �m�����z | ���� |
| ���z | binom |
| �|�A�\�����z | pois |
| ��l���z | unif |
| ���K���z | norm |
| �R�[�V�[���z | cauchy |
| �J�C��敪�z | chisq |
| t���z | t |
| F���z | f |
| �w�����z | exp |
| ���z | geom |
| �����z | hyper |
| �K���}���z | gamma |
��̓I�Ȋm�����z�ɑ���m�����x�����̖��̂́C
���K���zN(m,s)�̏ꍇ�͎��̂悤�ɕ\����܂��D�ʂȊm�����z�̏ꍇ�́C
�unorm�v�̉ӏ�����L�̖��̂Œu�������܂��D
| ���� | R�ł̖��� |
| �m�����x��(pdf) | dnorm(x,m,s) |
| �ݐϕ��z��(cdf) | pnorm(x,m,s) |
| ���ʊ�(quantile) | qnorm(q,m,s) |
| ��������(random) | rnorm(n,m,s) |
�ʂɃp�b�P�[�W��ǂݍ��܂���ƁC����ɑ��l�Ȋm�����z��
�������Ƃ��ł��܂��D�ǂ̂悤�Ȋm�����z�𗘗p�ł��邩��
���L���Q�Ƃ��Ă��������B
�ȉ��ł͕W�����K���zN(0,1)�̏ꍇ�̃O���t���m�F���܂��D
���̏ꍇ�̊m�����x���́udnorm(x)�v�����ł悭�A
�uplot�v�ɂ��O���t�͉��}�̒ʂ�ł��D
plot(dnorm, \(\small -\)4,4)
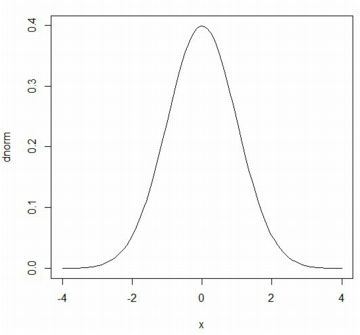
plot(pnorm,\(\small -\)4,4)
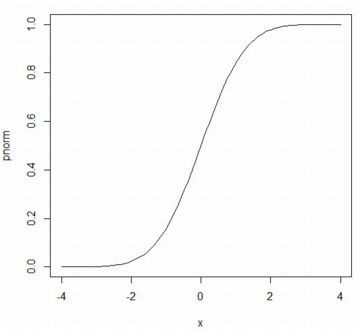
���}�́C\(\small {\rm P}(X\leq 1.96)=0.9750021\) �ł��邱�ƁC
�uqnorm�v�𗘗p����Ƌt�̊W�������邱�Ƃ�������Ă��܂��D
�f�t�H���g�ł́ulong.tail=TRUE�v���ÖقɎw�肳��Ă��܂��D
�ulong.tail=FALSE�v���w�肷��ƁC
\(\small {\rm P}(X\geq x)=q\) �̒l���Ԃ���܂��D
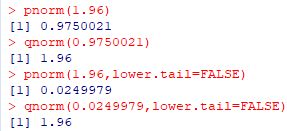
���� \(\small m\)�C�W���� \(\small s\) �̐��K���z�̊m�����x���́C
�udnorm(x,m,s)�v�ƈ����𑝂₷���ƂɂȂ�܂����C
���̊��� \(\small x\) ���܂�ł���̂�
�uplot�v�ŕ`�悷�邱�Ƃ͂ł��܂���D���̏ꍇ�́ucurve�v�𗘗p���܂��D
curve(dnorm(x,50,10),0,100)
�X�̊m�����z�ł̈����̗^�����͉��L�ɂ܂Ƃ߂��Ă��܂��D
|
|
�����̗��p
���K���z�̏ꍇ�́C�urnorm(n,m,s)�v�ɂ��C
����\(\small m\)�C�W����\(\small s\) �̐��K���z�ɂ�������������
\(\small n\) ��������܂��D
���}�́C
N(50,10)�ɂ�����������100����Ȃ�x�N�g���� \(\small x\) �Ƃ��āC
�������ɐ��Ōq���ŃO���t���������̂ł��D

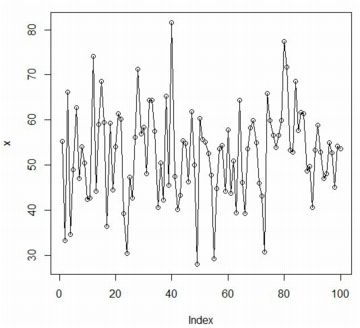
�����𗘗p����ƁC��̊m�����z�ɂ��������m���ϐ���
���ς��ǂ̂悤�ȕ��z�����邩���V�~�����[�g���邱�Ƃ��ł��܂��D
���݂ɁC
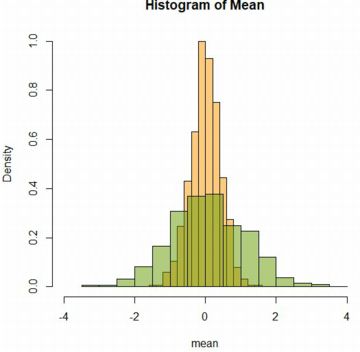
�W�����K���zN(0,1)�ɂ�����������(rnorm)5�̕��ς�1000�쐬���āC
���̃q�X�g�O������`���Ă݂܂��傤�D
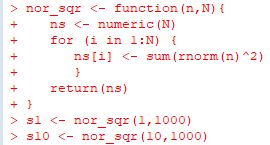
�܂��C���̂悤�ȃx�N�g��������������unor_mean�v�Ƃ��Ē�`���܂��D

��L�ł́C�unumeric(N)�v�ɂ��0��������Ȃ钷����N�̃x�N�g��������
�unm�v�Ƃ��܂��D�����āC�urnorm(n)�v�ɂ��
N(0,1)�ɂ������� n�̗����������āC���̕��ς� nm[i] �Ƃ��Ă��܂��D
�unor_mean�v�𗘗p���āC
�um1�v��N(0,1)�ɂ�����������1��������Ȃ�v�f��1000�̃x�N�g���Ƃ��C
�um5�v��N(0,1)�ɂ�����������5�̕��ς���Ȃ�v�f��1000�̃x�N�g���Ƃ��܂��D
���ꂼ��̃q�X�g�O�������d�˕`������ƁC���}�̂悤�ɂȂ�܂��D
�umain�v�ɂ��C�O���t��ʏ㕔�̃^�C�g�����w�肷�邱�Ƃ��ł��܂�.
�����ł̐F�w��̓J���[�R�[�h��p���܂����D
�F���̂�"#ff9900"�Ŏw�肳��܂��D
���̌��"80"�́C�F���d�˂��Ƃ��̓����x���w�肵�Ă��܂��D

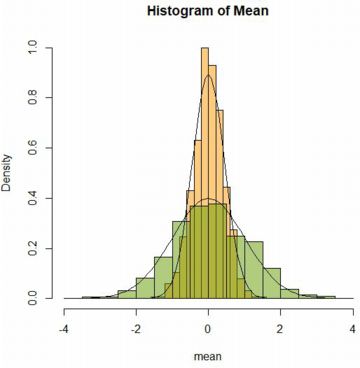
�O�̂��߁A�m�����x�Ȑ����d�˂Ă݂܂��D
���m�̂悤�ɁC�W�����K���z N(0,1) �ɂ�������
���� \(\small n\) �̕��ς́C���K���z N(0,\(\small 1/\sqrt{n}\))
�ɂ��������܂��D

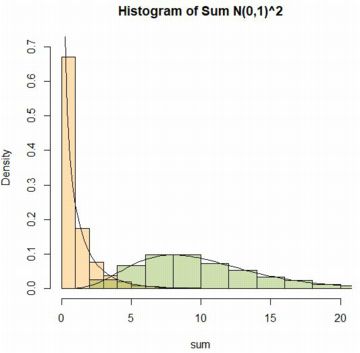
���l�ɂ��āCN(0,1)�ɂ����������� n�̕����a���l���܂��D
���m�̂悤�ɁC���̕��z�͎��R�x n �̃J�C��敪�z�ɂ��������܂��D
���}�ł́C�����a����Ȃ�x�N�g������������`���āC
1��10�̘a����Ȃ�x�N�g�������Ă��܂��D
���ɁC�����̃q�X�g�O������`�悵�āC�m�����x��(dchisq)��
�d�ˍ��킹�܂��D

|
|
�q�X�g�O����(2)
3�ȏ�̃q�X�g�O�������ɕ\������ɂ́C
�_�O���t�����܂���O���t�̕����K���Ă��܂��D
�܂���O���t�ŕ`�悷��ɂ́ulines�v�𗘗p���܂��D�����́ulines(x, y)�v�ł��D
�ux�v�uy�v�͉����Əc���̑Ή�����x�N�g��������w�肵�܂��D

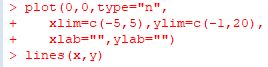
��L�͕����� \(\small y=x^2\) ���C��� \(\small [-4,4]\) ��0.1���݂ɂ���
�`�悵�悤�Ƃ������̂ł��D
���̌��ʂ́C���O�ɂǂ̂悤�ȃO���t��\�����������Ɉˑ����܂��D
�uplot�v��ucurve�v�́C�O���t��ʂ̊O�g��ݒ肵�ăO���t��`�悵�܂����C
�ulines�v�ɃO���t��ʂ̊O�g��\������@�\�͂���܂���D
���łɐݒ肳��Ă���O���t��ʂɏ�������邾���Ȃ̂ŁC
����ȑO�ɃO���t��\�����Ă��Ȃ���ԂŁulines�v�����s�����
�u�G���[�v�ɂȂ�܂��D
�O���t��\�����Ă��Ă��C�͈͂�����Ȃ��Ƃ��̓O���t�͕\������܂���D
�����ŁC�܂��C�O���t��ʂ̊O�g������\�������āC���̏�Łulines�v��
���s���܂��D
���}�ɂ�����utype="n"�v�̎w��́C�O�g�����ݒ肵�ĉ����`�悵�Ȃ��悤��
���邽�߂̐ݒ�ł��D���̎w������Ȃ��ƁC
�uplot�v�̍ŏ��Ŏw�肵���_ (0,0) �̉ӏ��ɔ��ۂ��z�u����܂��D
�uplot�v�ucurve�v�͍�������}���ƌĂ��̂ɑ��āC
�ulines�v�͒ᐅ����}���Ƃ��Ă��܂��D
���́ulines�v�𗘗p���ăq�X�g�O������܂���ŕ`�悷��ɂ́C
�q�X�g�O�����̊K���l�Ȃǂ̃f�[�^���K�v�ł��D
���̃f�[�^�́uhist�v�����s����Ɠ����܂��D
���Ƃ��C���K���zN(50,10)�ɂ�������������1000���������āun1�v�Ƃ���.
�ŏ��l�ƍő�l�ׂ邱�Ƃɂ��C[20,75] �̋�Ԃ�5���݂ɕ�������
�q�X�g�O������`�悵�āuhn1�v�ɑ������ƁC
�q�X�g�O�����̏�uhn1�v�ɕۑ�����܂��D
�O���t���\������܂����C�����ł͕K�v�Ƃ��Ȃ��̂Ŗ������܂��D
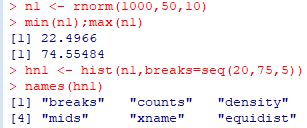
�unames(hn1)�v�Ƃ���1�s�ڂ̗�\��������ƁC
�uhn1�v��6��Ȃ�f�[�^�ł��邱�Ƃ�������A
�����_(breaks)�C�x��(counts)�C�m�����x(density)�C�K���l(mids)
�Ȃǂ��ۑ�����Ă��邱�Ƃ�������܂��D
���t�@�C���̃t�@�C����(xname)���ێ�����Ă���C
�s���̈قȂ�f�[�^�ɂȂ��Ă��܂��D
�o������6�s����\�������悤�Ƃ��āuhead(hn1)�v�Ƃ���ƁC
�e��̒l���ƂɑS���\�������̂ŁC
�����_�𑽂�����Ă���Ƃ��͒��ӂ���K�v������܂��D

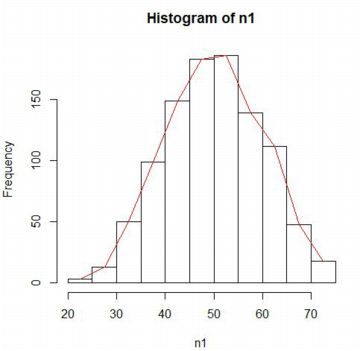
���̃f�[�^�𗘗p���ăq�X�g�O������܂���O���t��`�悷��ɂ́C
�ux�v�ɂ͊K���l(mids)���C�uy�v�ɂ͓x��(counts)���m�����x(density)���w�肵�܂��D
���}�ł́C�ŏ��ɕ\�����ꂽ�x���ɂ��q�X�g�O�����ɍ��킹��
�x���ŕ\�������܂����D
�Ȃ��C���}�́u���v�͑S�p�ł����C���ۂɂ͔��p�œ��͂��܂��D
lines(hn1��mids, hn1��counts, col="red")
�ȏ�̂��Ƃ𗘗p���āC
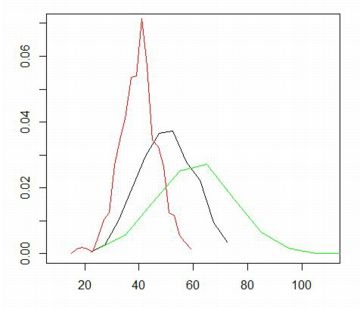
���}�ł�N(50,10), N(40,7), N(60,14)�ɂ�����������1000�̃q�X�g�O�������C
���ꂼ��̍��ݕ��� 5, 2, 10 �Ƃ��č쐬���܂����D
�un1�v�Ɓuhn1�v�͂��łɍ쐬�ς݂ł��D
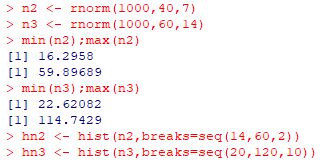
���}�́C�����̃q�X�g�O�����̃f�[�^��p���āC
3�̃q�X�g�O����������ŕ`�悵�����̂ł��D
�K���l�̉ӏ��ɓ_��z�u�������Ƃ��́utype="o"�v��NjL���܂��D
|
|
���S�Ɍ��藝�@�@[script]
�����̏ꍇ�C
���͂��悤�Ƃ����W�c�̓��v�ʂ��ǂ̂悤�ȕ��z�����Ă���̂��͕s���ł��D
����ׂ悤�Ƃ��āC�W�{���o���ĕW�{���ς�W�{���U���v�Z���C
���̒l�����Ƃɕ�W�c�̕��� \(\small \mu\) �╪�U \(\small \sigma^2\)
�𐄑����悤�Ƃ��܂��D
����炪���݂���ꍇ�C���S�Ɍ��藝�́C�W�{�̐���傫�����Ă����C
\[\small \lim_{n\to\infty}
{\rm P} \left(\frac{\bar{X_n}-\mu}{\sigma/\sqrt{n}}\leq x\right)
=\frac1{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{x^2}{2}}\,dx\]
�����藧���ƁC�܂�C�W�{���ς�W���������l�͕W�����K���z N(0,1)
�Ɏ������邱�Ƃ��q�ׂĂ��܂��D����́C�W�{����傫�����Ă����ƁC
�W�{���� \(\small \bar{X}\) �̕��z��
���K���z N\(\small (\mu, \sigma^2/n)\) �ɋ߂Â��Ă������Ƃ������Ă��܂��D
�ȉ��ł́C���̂��Ƃ��J�C���敪�z�Ŋm���߂Ă݂܂��傤�D
���J�C��敪�z
���R�x \(\small n\) �̃J�C��敪�z�́C�W�����K���z N(0,1) �ɂ�������
�݂��ɓƗ��� \(\small n\) �̊m���ϐ� \(\small X_1, X_2, \ldots,X_n\)
�ɑ��āC\(\small X=X_1^2+X_2^2+\cdots+X_n^2\) �̕��z�ł���C
���ςƕ��U�͂��ꂼ�� \(\small E(X)=n, V(X)=2n\) �ł��D
�uR�v�ł̃J�C��敪�z�̖��̂́uchisq�v�ł���̂ŁC
�m�����x���́udchisq(x,���R�x)�v�C���������́urchisq(��, ���R�x)�v�ł��D
���}�́C���R�x�� 1(��), 2(��), 5(��), 10(��)�� �ꍇ��
�J�C��敪�z�̊m�����x���̃O���t�ł��D
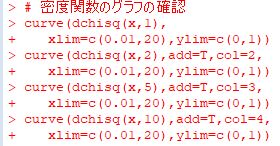
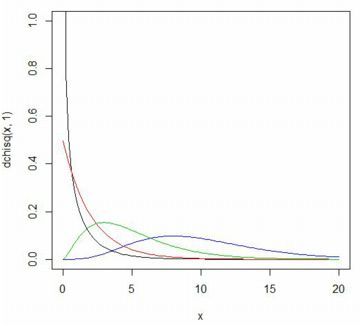
���K���z�Ƃ͎��Ă������Ȃ����z����̒��o�Ƃ��邽�߁C
���R�x (degree of freedom) �� df=1 �̏ꍇ���l���܂��D�ŏ��ɁC
�e�v�f�� \(\small n\) �̗������ς���Ȃ�x�N�g������������`���āC
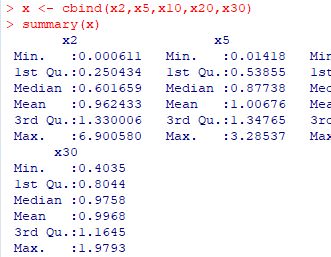
�W�{���� 2, 5, 10, 30 �̕��ς���Ȃ�v�f�� 1000�̃x�N�g�������܂��D

��x�N�g���ɂ܂Ƃ߂āusummary�v�����s���čŏ��l��ő�l���m�F���܂��D
�usummary�v��5���v��̂��ƂŁC
�ŏ��l�E��1�l���ʐ��E�����l�E��3�l���ʐ��E�ő�l��5��
�ɉ����ĕ��ς��\������܂��D
���ɁC���ݕ��� 0.2 �Ƃ����q�X�g�O���������擾���܂��D

��������ƂɁC�W�{���� \(\small n=2, 5, 10\) �̏ꍇ�̃q�X�g�O������
�܂���ŕ`�悷��Ǝ��̂悤�ɂȂ�܂��D
���ς��Ƃ�W�{���𑝂₵�Ă����ƍ��E�Ώ̂̎R�`�ɂȂ��Ă����̂�������܂��D


���ɁC���������x�N�g�� x2, x5, x10 ��W���������x�N�g���ɑ��āC
�����悤�ȃq�X�g�O������`�悵�܂��D
��W�c�͎��R�x�� df=1 �̃J�C�j�敪�z�ł���̂ŁC
E(X)=n=1, V(X)=2n=2 �ł���C
�W�{�� \(\small n\) �̏ꍇ�̕W�{���ς� \(\small 2/n\) �ł��D

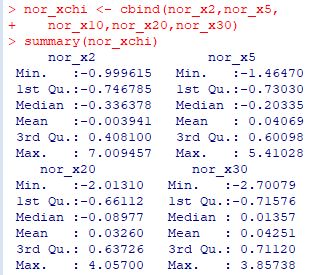
�W���������x�N�g���̃q�X�g�O���������擾���܂��D

���̒l�����ƂɁC5, 10, 30�̏ꍇ�̃O���t��܂���ŕ`�悵�܂��D
�W�{����������ɂ��������C���E�Ώ̂̌`�ɋ߂Â��Ă����̂�������܂��D

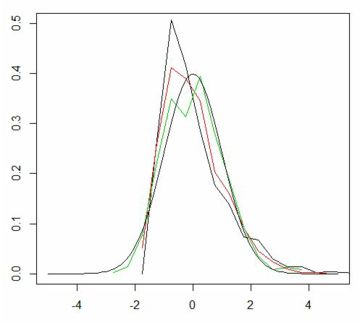
�W�{��30�̏ꍇ�́C���ς� 1�C���U�� \(\small \frac2{30}\) �̐��K���z��
�ߎ��ł��܂��D���}�ł́C���̂��Ƃ�W�������Ȃ��Ŋm�F���܂��D

�����ς╪�U�����݂���悤�Ȋm�����z�ł́C���̕��z�ł����l�ɂ��āC
�W�{���ς�W��������ƕW�����K���z N(0,1) �ɋ߂Â��Ă������Ƃ�
�m�F���邱�Ƃ��ł��܂��D
�����ς╪�U�����݂��Ȃ��悤�Ȋm�����z������܂��D
���̂悤�ȏꍇ�̒��S�Ɍ��藝�ɑ���������̂Ƃ��āC
��ʉ����S�Ɍ��藝������C���K���z�ɑ�����蕪�z���d�v�Ȉʒu���߂Ă��܂��D
�ڂ����́u�������v��
�Q�Ƃ��Ă��������D
|
|
ggplot2�̎g����
�uR�v�̃O���t�\���́A���U�f�[�^�́uplot�v�C
�A���Ȑ��́ucurve�v�𗘗p���邱�Ƃ�
���푽�ʂȃO���t��`�悷�邱�Ƃ��ł��܂��D�������C
���̖ڐ���̐U����ȂǁC�ׂ����d�l�ɕs���������邱�Ƃ�����܂��D
���̂悤�ȂƂ��́uggplot2�v�𗘗p����悢�ł��傤�D
��ggplot2�̃C���X�g�[��
�uggplot2�v�͕W���ł͊܂܂�Ă��Ȃ��̂ŁC
�V���ɃC���X�g�[������K�v������܂��D
�uinstall.packages("ggplot2")�v�ɂ��C�C���X�g�[���ł��܂��D
���̃p�b�P�[�W�́C
Rstudio�̊J�����ł�����Posit�Ђ́utidyverse�v�Ƃ����p�[�P�[�W��
�܂܂����̂ł��Dggplot2�P�̂ł��C���X�g�[���ł���悤�ł��D
�C���X�g�[����́C�ulibrary(ggplot2)�v�ɂ�藘�p�\�ɂȂ�܂��D
�{���́C�utidyverse�v���C���X�g�[�����ׂ����Ǝv���܂����C
���������ggplot2�ȊO�ɂ������̃p�b�P�[�W���ǂݍ��܂�܂��D
������ƁuR�v�����������̐g�Ƃ��ẮC�����͍���g�������ɂȂ��̂ŁC
�����ł́uggplot2�v�������C���X�g�[�����܂����D
�������Cggplot2�P�̂ł��C�c��ȃR�}���h��I�v�V����������܂��D
���̑S�e�́C
ggplot2�̊J���w�ɂ�鉺�L�̉����(�p��)���݂Ă��������D
�@�Ȃ��C�utidyverse�v�́C
�f�[�^�T�C�G���X�Ɍg�����ɂƂ��Ă�
�K�{�̃p�b�P�[�W�ł���悤�ł��D
Web��������ƁC���낢��ȉ���T�C�g���\������܂��D
�Q�ƃ����N�ł́C�����̊�����Ƃ�܂Ƃ߂܂����D
�܂��C�X�̃R�}���h�̏ڍׂ́C
�uFunction Reference�v(�p��)�ɃA�N�Z�X���āC
�E��ɕ\�������3�{���̃��j���[����uSerch for�v�̉ӏ��Œ��ׂ邱�Ƃ��ł��܂��D
�g�����̉��(�p��)�̌㔼�Ɋ���̃T���v���R�[�h���\�������̂ŁC
������Q�l�ɂ���悢�ł��傤�D
�ȉ��ł́C��Ɋm�����x�Ȑ��𗼑ΐ��O���t�ŕ`�悷�邱�Ƃ�ڕW�Ƃ��āC
���������ł��������ɂ��Đ������܂����C
���ɂ����낢��Ȃ���������悤�Ȃ̂ŗ��ӂ��ĉ������D
��ggplot2�̃f�[�^�^
ggplot2���C���X�g�[������ƁC�T���v���f�[�^�Ƃ��āuiris�v�Ƃ���
�f�[�^�Z�b�g���C���X�g�[������܂��D
����́C�Ԃ́u�A�C���X�v�̏����܂Ƃ߂��t�@�C���ł��D
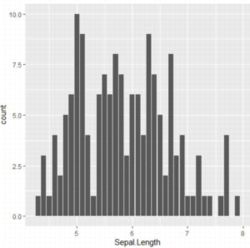
�f�[�^�̊T�v�́ustr(iris)�v�ɂ��\������܂��B
�uiris�v�������ƑS���(150�s)���\������Ă��܂��̂Œ��ӂ��ĉ������C
�usepal�v����(����)�ЁC�upetal�v�͉ԕقŁC
���ꂼ��̒����ƕ��̏����܂��D
�uspecies�v�͎�̂��ƂŁC
iris�Ƃ����Ԃ̎�ނɊւ��镶����������܂�Ă��܂��D

�ustr()�v�̓f�[�^�̍\��(structure)��\�����܂��D
1�s�ڂ���C�f�[�^�̌^�̓f�[�^�t���[���^�ł���C
5�̕ϐ�(��)������150�̃f�[�^�����邱�Ƃ�������܂��D
���̉��ł́C�e��̗ƁC�ϐ��̌^�C�����čŏ���5�̒l���\������Ă��܂��D
�ŏ���4��͐��l�ϐ�(numeric)�ŁC
5��ڂ͕�����(character)�ł��邱�Ƃ�������Ă��܂��D
�uhead(iris)�v�Ƃ��Ă��Əo������6�̃f�[�^���\������܂����C
�u�f�[�^�^�v�ɂ��Ă̕\���͂���܂���D
���̂悤�ɁCggplot�ł̃f�[�^�^�́C
�f�[�^�t���[���^�ł���K�v������̂Œ��ӂ��K�v�ł��D
���̃f�[�^�^�́C1�s�ڂ͊e��̃f�[�^���ŁC
2�s�ڈȍ~�ɌX�̃f�[�^������܂��D
���̌^�̓����́C���l��╶����A���邢�͐^�U���̘_���l�������
��ɂ܂Ƃ߂��f�[�^�Ƃ��Ĉ������Ƃ��ł���Ƃ������Ƃł��D
���͂��悤�Ƃ���f�[�^�̌^��m��ɂ́uclass()�v�𗘗p���܂��D
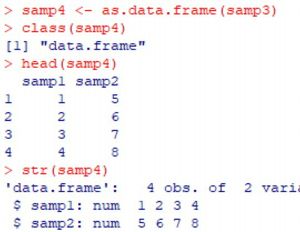
���}�́C2�̃x�N�g��(samp1, samp2)���ucbind�v��
�܂Ƃ߂��f�[�^(samp3)�ɂ��C
����class()�Chead(), str()�̌��ʂ����������̂ł��D

�f�[�^(samp3)���f�[�^�t���[���^�ɕϊ�����ɂ�
�uas.data.frame()�v�𗘗p���܂��D
���}�́C�f�[�^�t���[���^�Ƃ����f�[�^(samp4)�ɂ��C
class()�Chead()�Cstr()�̌��ʂ����������̂ł��D
samp3��samp4�̈Ⴂ�ɂ��āC�悭�c�����Ă��������D
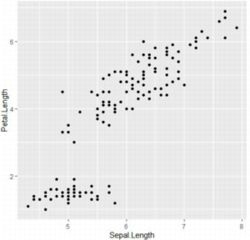
�����U�f�[�^�uiris�v�̃O���t
�ŏ��ɁC�T���v���f�[�^�ł���uiris�v�𗘗p���āC
sepal��petal�̒����Ɋւ���U�z�}��`�悵�Ă݂܂��傤�D
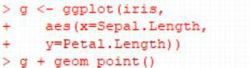
�`��R�}���h�́uggplot�v�ŁC�ŏ��Ƀf�[�^�������āC
�uaes�v�ʼn����Əc���̃��x�����w�肵�܂��D
�uaes�v�́uaesthetics�v�̗���ŁC���h���Ɋւ���
���낢��Ȏw����s���܂��D
�����ł́C���̃��x����ݒ肵�Ă��܂��D
���̏ł͐}�͕`�悳��܂���D
���ۂ̃f�[�^�Ɋ�Â��Ĕ͈͂�������������C
���̃��x�����������܂ꂽ�}���ug�v�ƒ�`����C
�Ƃ����w�肪�s��ꂽ�����ł��D
�����Łuprint(g)�v�Ƃ���ug�v�̐}���\������܂����C
�����Əc���Ƀ��x���̐U��ꂽ�}���\������邾���ł��D
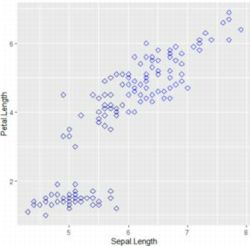
�U�z�}����������邽�߂ɂ́C
�ug+geom_point()�v�Ƃ��܂��D
�Y������_������������Đ}���\������܂��D
�ug ��- g+geom_point()�v�Ƃ���C�������܂ꂽ�}��
���߂āug�v�Ƃ��邾���ŁC�}�͕\������܂���D
�Ȃ��C�u���v�͎��ۂɂ͔��p�ł����C���̕��ł͑S�p�𗘗p���Ă��܂��D
|
|
|
�����܂ł̐}��̂ɁC�ʂȂ���������܂��D

����́C�ŏ��Ɂuggplot()�v�ŋ�̐}������āug�v�Ƃ��āC
����ɏ������ꂽ���̂����߂āug�v�Ƃ��Ă��܂��D
�Ō�Ɂuprint(g)�v�Ƃ��Ȃ��Ɛ}�͕\������܂���D
�}�͑O�̐}�Ɠ����Ȃ̂ŏȗ����܂��D
�擪���ugeom_�v�̃I�v�V�����𗘗p����ƁC���낢���
�}��`��ł��܂��D���L�ȊO�ɂ���������܂��D
- geom_point() �F �U�z�}
- geom_bar() �F �_�O���t
- geom_line() �F �܂���O���t
- geom_boxplot() �F ���Ђ��}
- geom_errorbar() �F �덷�_�O���t
- geom_histgram() �F �q�X�g�O����
- geom_density() �F �m�����x�Ȑ�
- geom_violon() �F �o�C�I�����v���b�g
�U�z�}�������C�f�[�^��1��ނ����ɂȂ�܂��D
�Q�l�܂łɁC�_�O���t�̗����Ă����܂��D

���̃��x���ȊO�̎w��Ƃ��ẮC
���Ƃ��ugeom_point()�v�̊��ʓ��Ŏ��̂悤�Ȃ��Ƃ��w��ł��܂��D
���ɂ����낢��Ȃ��Ƃ��w��ł��܂��D
- colour �F �F(�֊s)
color�ł����܂�Ȃ��D
- fill : �F(�h��Ԃ�)
- size : �傫��
- shape : �_�̌`��
���Ƃ��C���L�̂悤�Ȍ`�ł��D
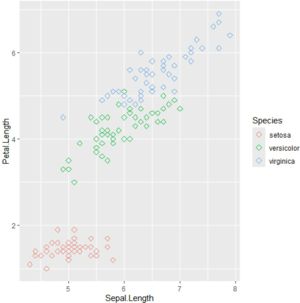
�ugeom_point(aes(color=Species))�v�Ƃ���ƁC���}�̂悤�ɁC
�Ԃ̎�ނ��ƂɎ����I�ɐF���ς��܂��D
�ugeom_point(aes(shape=Species))�v �Ƃ���ƁC
�_�̌`�������I�ɕς��܂��D

���ɂ��C���낢��ƍׂ����w������邱�Ƃ��ł��܂��D
���̍��ڂ̍Ō�ɏЉ�郊���N����Q�Ƃ��Ă��������D
|
|
|
�����̃O���t
���̃O���t��`�悳����ɂ́C
�ustat_function(fun=�E�E�E)�v�𗘗p���܂��D

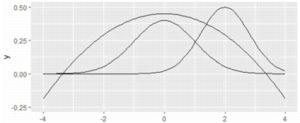
���ɐ�������ƁC�ŏ��̍s�ł́C
��̐}�ɉ����Əc���͈̔͂��w�肵�Ă��܂��D
�Ȃ��CR�̃X�N���v�g�ŁC
�u+xlim(-4,4)�v�̉ӏ��ʼn��s���Ď��s����ƃG���[�ɂȂ�܂��D
�u+�v���擪�ɂȂ�Ȃ��悤�ɉ��s���Ă��������B
2�s�ڂ�N(0,1)�C3�s�ڂ�N(2,0.8)�̃O���t��`���Ă��܂��D
N(m,s)�̏ꍇ�́uarg=list(mean=m, sd=s)�v�̌`��
�������w�肷�邱�ƂɂȂ�܂��D
3�ڂ́C2���� \(\small -0.04x^2+0.45\) �̃O���t�ł��D
�ufun=function(x) �v�̌�ɁC���̎��ڏ������݂܂��D
�ŏ��Ɏw�肵���͈͓��Ɏ��܂�Ȃ������́C
�폜�����|�̌x�����b�Z�[�W���\������ĕ`�悳��܂��D
�@�Ȃ��C���̒�`�́Cggplot() �̑O�ŁC���Ƃ��C
�uf ��- function(x) ���̎��v�Ƃ��Ă����āC
�ustat_function(fun=f)�v�Ƃ���������܂��D
�ufunction(x)�v��1�ϐ����ł����C
�ufunction(x,y)�v�Ƃ����2�ϐ������`�ł��܂��D
�ustat_function�v�̑��Ɂugeom_function�v�����p�ł��܂��B
���}�ł́C�F�����Ă݂܂����D
�F�̎w��́C�ucolor�v�ucolour�v�̂ǂ���ł����܂��܂���D
�O�҂͕č��p��C��҂͉p���p��ł��D

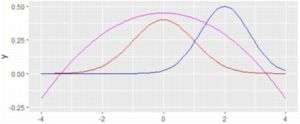
�ustat_function�v�𗘗p����ƁC�ugeom�v�I�v�V���������p�ł��āC
�Ȑ���_��ŕ`������C�h��Ԃ����肷�邱�Ƃ��ł��܂��D
�܂��C�uxlim�v�𗘗p���āC�`��͈̔͂�ς��邱�Ƃ��ł��܂��D

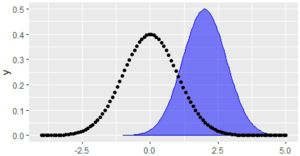
��}�̂悤�ɁC�ugeom�v�I�v�V�����ɁC
�upolygon�v���w�肷��Ɠh��Ԃ��C
�upoint�v���w�肷��Ɠ_��ŕ\������܂��D
�ufill�v�ɂ��h��Ԃ��̐F���w�肵�Ă��܂��D
N(0,1)��N(2,0,8)�̕`��̏����t�ɂ���ƁC
(���̊��ł�)������ƕςɕ\������܂����D
|
|
|
�����낢��Ȑݒ�
(1) ���̃��x��
�O�̐}���݂�ƁC�c���ɂ� \(\small y\) �Ƃ������x�������Ă��܂����C
�����ɂ͉������Ă��܂���D
���̃��x���́C�uxlab�v�uylab�v�Œ������邱�Ƃ��ł��܂��D
(2) ����Ƒ���
�Ȑ��̐���́ulty�v�C�����́usize�v�Ŏw��ł��܂��D
����������Ŏw�肵�āC
�u1:�����v�u2:�j���v�u3:�_���v�ł��D
(3) �e�L�X�g�̑}��
�O���t�̒��Ƀe�L�X�g��}������ɂ�
�uannotate�v���g�p���܂��D�}���ʒu���m�肷��ɂ́C
����Ȃ�̎��s���낪�K�v�ł��D
(4) ���̖ڐ���
���̖ڐ��肪�C�ɓ���Ȃ��Ƃ��C
�Ⴆ�� \(\small x\) ���� 1���݂ɂ������Ƃ��́C
�uscale_x_continuous()�v�𗘗p���C
()���Łubreaks=seq(-4,5,length=10))�v
�ȂǂƂ��܂��D�useq�v���g�p���Ȃ��ŁC
�uc(-4,-3,...,4,5)�v�Ƃ��Ē��ڎw�肷�邱�Ƃ��ł��܂��D
�ȏ�𗘗p���ďC�������̂����}�ł��D


|
|
���ΐ���
�����ł́C����ΐ����Ƃ����O���t�ɂ��čl���܂��D
���}���K���}���̃O���t�ł��D

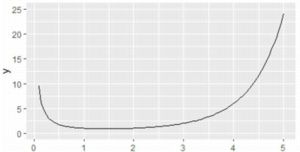
�K���}�� \(\small \Gamma(x)\) �� \(\small x>0\) �Œ�`�����̂ŁC
\(\small [0.1, 5]\) �Ŏw�肵�܂����D
\(\small \Gamma(5)=4!=24\) �ł��D
���̊��� \(\small [0.1,10]\) �͈̔͂ŕ`�悵�悤�Ƃ���ƁC
\(\small \Gamma(10)=9!=362680\) �ƂȂ�̂ŁC
�ʏ�̖ڐ���ł͕`��ł��܂���D
�����ŁC\(\small y\) ����ΐ����ɂƂ�ƁC
\(\small \log 9!=5.56\) �ƂȂ蕁�ʂ̒l�ɂȂ�܂��D
���W����ΐ����Ƃ���ɂ́C
�uscale_y_log10()�v�ɂ��w�肵�܂��D

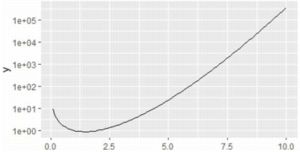
�ubreaks�v���Ȃ��āuscale_y_log10()�v�����ɂ���ƁC
�ڐ���͎����ł���
1e+01, 1e+03, 1e+05 �����ɂȂ�܂��D
scale_y �𗘗p���� \(\small y\) ���̖ڐ���C
���������ďc���͈̔͂𐧌䂷��̂ŁC
�ŏ��́uylim()�v�̎w��͕s�v�ł��B
�c���ƁC�d�����Ďw�肳��Ă���Ƃ��ăG���[�ɂȂ�܂��D
�ΐ����ɂ͂Ȃ�܂������C�u1e+0n�v�̂悤�ȕ\�L�͌��Â炢�ł��D
\(\small 10^n\) �̌`�ŕ\������ɂ́C
�V���Ɂuscales�v���C���X�g�[�����āC
�utarns_format()�v���g�p���܂��D

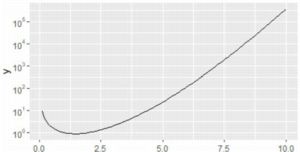
�ڐ���� \(\small 10^n\) �̌`�ɂ��邱�Ƃɂ������Ȃ���C
�uscale_y_continuous(trans="log10")�v�Ƃ��邱�Ƃł�
���܂��܂���D1, 10, 100,...�̌`�ŕ\������܂�(�}�͗�)�D
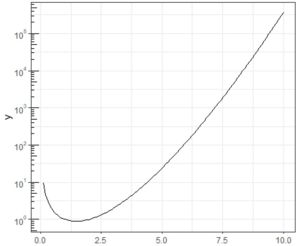
�����܂ł���ƁC�ׂ����ڐ�����~�����Ȃ�܂��D
�uannotation_logticks()�v�Œlj��ł��܂��D
�O�i�����͑O�}�Ɠ��l�ł��D


�}���c�ɐL�тĂ��܂����C�ׂ����ڐ��肪���₷���悤�ɁC
�O���t�E�B���h�E���蓮�ŏc�ɐL���܂����D
�usides=�v�ŁC���̂ǂ̏ꏊ�ɓ���邩���w�肵�܂��D
�����ł͍���(light)�ɓ����悤�Ɏw�肵�Ă��܂��D
�w�肵�Ȃ��Łu()�v�����ɂ���ƁC�����Ɖ����ɂ��܂��D
����́usides="lb"�v���w�肵�����ƂɂȂ�܂����C
�����͑ΐ����ł͂Ȃ��̂ō��������ɕ\�������悤��
�w�肷��K�v������܂��D
���̐������ꂽ���Ȃ��Ă��܂��D
�utheme_bw()�v��lj�����悢�悤�ł��D
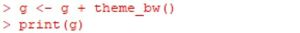
|
|
|
�����ΐ���
���łɁC���ΐ����ŕ`�悵�Ă݂܂��傤�D
���}�́C�W�����K���zN(0,1)[��]�C���R�x2�� \(\small t\) ���z[��]�C
�����ĕW���R�[�V�[���zCauchy(0,1)[��] �̊m�����x�Ȑ����C
\(\small x>0\) �͈̔͂ŕ��ʂɕ`�������̂ł��D

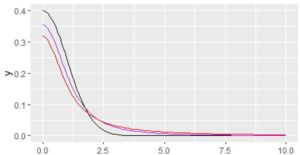
�Ȃ��CN(0,1)��Cauchy(0,1)�̏ꍇ�́C�uargs�v�ɂ������͕s�v�ł��D
��̓I�Ȏ��������ƁC���ꂼ�ꎟ�̂悤�Ȏ��ɂȂ�܂��D
\[
\begin{array}{rl}
\small
N(0,1):=&\small \dfrac1{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\\
\small t(2):=&\small \dfrac1{\sqrt{2\pi}}\Gamma\left(\dfrac32\right)
\left(1+\dfrac{x^2}{2}\right)^{-\frac32}\\
\small {\rm Cauchy}(0,1):=&\small \dfrac1{\pi}\dfrac{1}{1+x^2}
\end{array}\]
�o�����̍����ł͈Ⴂ��������܂����C
�E�������ł͏d�Ȃ��Ă��܂��ĈႢ���悭������܂���D
\(\small x\) ���傫���ӏ��̈Ⴂ������ɂ́C
���ΐ����Ƃ��ĕ`�悷��K�v������܂��D
�O���ŏq�ׂ��c���̏ꍇ�̂��Ƃ������ɂ��K�p���ĕ`�悷��ƁC
���̂悤�ɂȂ�܂��D
\(\small x\) ���͈̔͂� \(\small [10^0,10^2]\)�C
\(\small y\) ���͈̔͂� \(\small [10^{-5},10^0]\) �Ƃ��Ă��܂��D

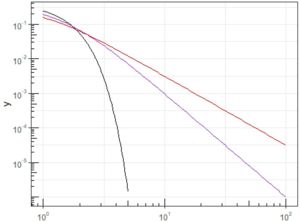
�����ȂƂ���C���̐}��܂łɌ��\�Ȏ��s����̎��Ԃ��₵�܂����D
�uscale_�v�̉ӏ��Ŕ͈͂��w�肵�Ă��C�O���t�����͈̔͂��Ă��܂���
�v���悤�Ȑ}�������܂���D
�����ŁC�ustat_function�v���Łuxlim�v�ɂ��O���t�͈̔͂𐧌����܂����D
\(\small x\) ����ΐ����Ƃ����ꍇ�́C
�uxlim�v�͈̔͂� \(\small 10^n\) �̎w�� \(\small n\)
�͈̔͂ł��邱�ƂɋC�t�����܂łɂ��Ȃ�̎��Ԃ�v���܂����D
N(0,1)�͎w�����ŋ}���Ɍ�������̂ŁC�͈͂� \(\small [10^0,10^{0.7}]\)
�Ƃ��Ă��܂��D\(\small 10^{0.7}\approx 5.01\)�ł��D
�����菬�����ƃO���t���r���Ő�C�傫���� scale_y �Ŏw�肵���͈͂�
�����Ă��܂��đS�̂̃o�����X������Ă��܂��܂��D
|
|
|
���uggplot2�v�Q�ƃT�C�g
|
|