-
はじめに・目次
-
グラフ電卓「TI-Nspire CX CAS」は,
それまでのTIの電卓が進化したもので,
カラー表示可能が可能になっています.
ただし,キー操作やファイル構造が大きく変更されました.
従来のTIの電卓と比べると最初はちょっと使いにくいのですが,
薄い筐体にCBL機能が標準で組み込まれて実データの収集も
手軽にできるなど,従来機種と比べると機能が大きく向上しています.
この電卓を初めて手にすると,
高機能であるが故の使いにくさを感じるかもしれません.
たとえば,電源を入れても,
関数電卓のようにすぐに計算できる状態にはなりません.
パソコンのように,立ち上がるのを待つ必要があります.
一方では,エクセルのシートを追加していくような感じで,
いろいろな操作を切り分けて保存しておくことができます.
これは,一つのテーマで継続的にいろいろな計算を推し進めていったり,
収集した実データにいろいろな解析を加えたりする場合は
非常に便利な機能です.ただし,
その機能を操るには,ページ・プロブレム・ドキュメントについて
理解しておく必要があります.
たとえば,
nspiremanと名付けたドキュメントについて,
下図の上段では1番目のプロブレムの内容が、
下段では2番目のプロブレムの内容が示されています.
1番目のプロブレムは3つのページを持ち,
そこではいろいろな式の計算を行っています.
2番目のプロブレムは2つのページを持ち,
1つ目のページでは関数 \(\small f(x)\) を定義して,
2つ目のページでそのグラフを表示しています.
これらを1つのドキュメントとして保存することができるのです.
1つのドキュメントは30のプロブレムを持つことができ,
1つのプロブレムには50ページまで登録することができます.
したがって,TI-Nspireを傍らに置きながら数学の本を読むとき,
章や節ごとの操作をプロブレムやページに分けながら記憶させて
おくことができるのです.
一方で,操作履歴を保存する必要はなく,
その場でちょっと計算したい,
あるいはちょっとグラフを確かめたい,
というときがあります.そのようなときは,
プロブレムやページを気にすることなく,
簡単に計算やグラフ描画を行う機能も用意されています.
この冊子では,
もやは「小さなコンピューター」というべき
「TI-Nspire CX CAS」の使い方について解説します.
この電卓を「思考のツール」として活用した場合は,
皆さんの前には無限の可能性が開かれてくるでしょう。
TI-Nspireの持つ豊富な機能を使いこなし,
数学の学習に役立ててください。
-
この冊子の使い方
この冊子では、数学の学習を進めるにあたって,
TI-Nspire CX CAS (以下,「Nspire」と略称する)の使い方について解説します。
このグラフ電卓は数式処理(Computer Algebra System, CAS)を行うことができ,
文字式の計算,微分積分の計算,行列に関する諸計算,
空間曲面の描画を行うことができます.
センサーを用意すれば即座に実データを取得することもできます.
PCデータとの連携を図ることも容易です.
数学の学習のみならず,
物理・化学の実験等のデータ解析を行うこともできるので,
Nspireをフル活用すれば
現実世界と数学との関わりについての理解を大きく向上させることができるでしょう.
どのようなことが可能になるか,その数学機能の概要は,
とりあえずは表5.2(第1章の36頁)
を見てください.
ただし,高機能であるがゆえに,
初めて手にしたときは使いにくさを感じるかもしれません.
この冊子では,このような機器を初めて操作する人を念頭に,
できるだけ分かりやすい解説を心がけました.
Nspireを手元におきながら,
現実世界を背後で統括している数学の世界を堪能してください.
第1章では,
Nspireのファイル構成や,
主要なキーの概要と操作手順など,Nspireの基本操作について解説しました.
この章は,最初に一通り目を通してください.
第2章以降の章は,
全てを一気に理解しようとする必要はありません.
それぞれの数学への関心の度合いに応じて,
目次や索引を見ながら必要と思われる部分を参照してください。
-
幾つかの注意事項
- キーの記号
この冊子では,Nspireのキーを完全に再現することは
できませんでした.下記の4つのキーについて,
本書の記号とNspireとのキーとの対応関係については,
特に注意してください.

- ページ・プロブレム・ドキュメント
Nspireを使いこなすには,
ページ・プロブレム・ドキュメントについての理解が不可欠です.
しかし,最初は,カタカナ語が氾らんしてよく分からないかもしれません.
「よく分からない」場合は,あまり気にする必要はありません.
必要とする機能は,
最初に表示されるHome画面下部にある7つのアイコンから選択してください.
Nspireは「Unsaved Document」を作って,
その中のページとして勝手に保存してくれます.
ページの操作方法だけ理解しておけば十分です.

-
第1章
基本操作
- 第1節 基本操作:
電源の入れ方・切り方
Home画面
- 第2節 ページ・プロブレム・ドキュメント:
ファイル構成とページの操作方法
- 第3節 計算画面での基本操作 :
四則計算と関数計算
各種キーの機能
- 第4節 グラフ画面での基本操作 :
グラフ、トレース、描画範囲
テーブル機能
- 第5節 カタログ機能 :
カタログ機能の種類と使い方
- 第6節 計算画面と数式テンプレート :
各種の数式テンプレートの使い方
-
第2章
代数計算での数学機能
- 第7節 数の計算:
素因数分解、最小公倍数
分数変換
商と剰余、複素数
- 第8節 式の計算:
方程式の解法、展開、因数分解
多項式の除算、左辺・右辺
-
第3章 微分積分での数学機能
- 第9節 微分積分の計算:
微分、積分、極限値、総和
接線、法線、長さ、陰関数
- 第10節 微分方程式の解法:
1階・2階・連立微分方程式
解曲線、勾配場、相平面
-
第4章 線形代数での数学機能
- 第11節 ベクトルの計算:
ベクトルの定義、内積、外積
座標変換
- 第12節 行列の計算:
行列の定義、基本変形、消去法
固有値、LU分解、QR分解
-
第5章
いろいろな曲線と曲面
- 第13節 媒介変数表示と極座標:
媒介変数を用いた関数のグラフ
逆関数x=f(y)のグラフ、
極座標を用いた関数のグラフ
- 第14節 陰関数のグラフ
- 第15節 不等式で表される領域
不等式で現れる領域
複数の不等式で表される領域
領域の境界と色
- 第16節 グラフ画面における諸操作:
グラフに対する操作
スライダーの利用
グラフ画面に対する操作
- 第17節 z=f(x,y)のグラフ:
2変数関数の式入力
グラフの回転と視点の方向
トレース機能、
曲面の媒介変数表示
-
第6章 ジオメトリーの幾何機能
- 第18節 幾何機能の概要:
幾何機能の概要
幾何機能のサブメニュー
- 第19節 幾何要素の配置:
点と直線の配置
(点・直線・接線・
ベクトル・円弧)
基本図形の配置
(円・多角形・楕円・
放物線・双曲線)
- 第20節 幾何要素の作図と変換:
幾何要素の作図
(中点・平行線・垂線・
二等分線等)
幾何要素の変換
(対称移動・平行移動
・回転・拡大・縮小)
- 第21節 幾何要素の計測:
長さ、面積、傾き、角度
計測機能の利用例
第22節 グラフ画面での幾何機能:
ジオメトリー画面とグラフ画面
グラフ画面での幾何機能の活用
-
第7章 リストデータと表計算
- 第23節 リストデータ:
リストデータの入力
列データの諸操作、乱数の利用
- 第24節 表計算:
表計算、列データのグラフ化
(ヒストグラム・箱ひげ図・
散布図)
-
第8章 いろいろな統計グラフ
- 第25節 統計プロット:
ドットとリストデータ
1変量リストのグラフ
2変量リストのグラフ
-
第9章 確率と確率分布での数学機能
- 第26節 確率の計算:
場合の数の計算、乱数の利用
リストデータの計算
- 第27節 いろいろな確率分布:
いろいろな確率分布
確率密度関数と分布関数
正規分布と中心極限定理、
二項分布
カイ二乗分布、t分布、F分布
-
第10章 統計回帰での数学機能
- 第28節 基本統計量:
1変量、2変量
- 第29節 線形回帰:
1次回帰(mx+b)、1次回帰(a+bx)
メディアンーメディアン法
- 第30節 いろいろな統計回帰:
3次・4次回帰、べき乗回帰
指数回帰、対数回帰、正弦回帰、
ロジスティック回帰、
多重線形回帰
-
第11章 推定・検定での数学機能
- 第31節 統計的推定:
統計的推定の考え方
いろいろな信頼区間
(母分散、母平均の差
母比率、母分散)
- 第32節 仮説検定:
仮説検定の考え方
Nspireによる仮説検定
いろいろな仮説検定
(母平均、母平均の差、母比率
適合度、独立性、等分散)
-
第12章 実データの収集と解析
- 第33節 センサーとVernier DataQuest:
センサーの種類、Nspireとの接続
DataQuest
- 第34節 Easy-Linkによる収集と解析:
Nspireとの接続
温度センサーによるデータ収集
他のアプリでのデータ利用
ニュートンの冷却の法則
- 第35節 CBR2による収集と解析:
CBR2の概要、測定上の留意事項
実データの収集、
特定部分の切り出し
CBR2単体でのデータ収集
- 第36節 Lab Cradleによる収集と解析:
Lab Cradleの概要
距離と光センサーの利用、
音センサーの利用
Lab Cradle単体でのデータ収集
-
第13章 Student Software
- 第37節 Student Software:
パソコンでの表示画面
ツールバー・ツールボックス
・スタイタスバー
Nspire本体との連携
ドキュメントの印刷、OSの更新
- 第38節 PublishView Document:
PublishView Documentの作成
PublishView Objectsの追加
第39節 Notes Application:
Notes Applicationの利用
Notesで利用できるツール
Notesでの編集機能
Notes枠のレイアウト
-
第14章 プログラミング
- 第40節 ライブラリー:
ライブラリーへの登録
計算画面でのプログラミング
- 第41節 TI-BASIC:
関数とプログラム
プログラムの作成
いろいろな制御コマンド
文字列の処理
サブルーチン、プログラム例
-
索引
- 補遺
- ■球面調和関数
掲示板[No.5]での質問を受けたことを契機に,
球面調和関数について調べてみました.
この関数は,球座標で考えたシュレディンガー方程式を
変数分離法を利用して解いて,
角度依存性のある部分を取り出したものです.
量子力学や電磁気学で現れるばかりではなく,
CGでのライティングや気象シミュレーションなど,
球面上の現象を解析するときには重要な関数であるようで,
次のように特殊関数を用いて定義される関数です。
\(\small l,m\) は整数で \(\small l\geq |m|\).
\[\small
\begin{align*}
Y_l^m(\theta,\phi)
&=(-1)^{\frac{m+|m|}{2}}\sqrt{l+\frac12}\\
&\times\sqrt{\frac{(l-|m|)!}{(l+|m|)!}}
P_l^m(\cos\theta)\\
&\times \frac1{\sqrt{2\pi}}e^{im\phi}
\end{align*}
\]
\(\small P_l^m(x)\) はルジャンドルの培関数と呼ばれる関数で、
次の式で表されます.
\[\small P_l^m(x)=(1-x^2)^{\frac{|m|}{2}}\frac{d^{|m|}}{dx^{|m|}}P_l(x)\]
\[なお,\small P_l(x)=\frac1{2^ll!}\frac{d^l}{dx^l}(x^2-1)^l\]
この関数は \(\small e^{im\phi}\) を含むので複素関数ですが,
その絶対値を取ることで3次元でグラフ化することができます.
\(\small P_l(x), P_l^m(x)\) を別々に定義するとエラーが表示されますが,
これらの導関数部分を一つにまとめて次の式で定義すると,
TI-Nspireでもこの関数のグラフを確かめることができます.
\[\small P_l^m(x)=\frac1{2^ll!}(1-x^2)^{\frac{|m|}{2}}
\frac{d^{l+|m|}}{dx^{l+|m|}}(x^2-1)^l\]
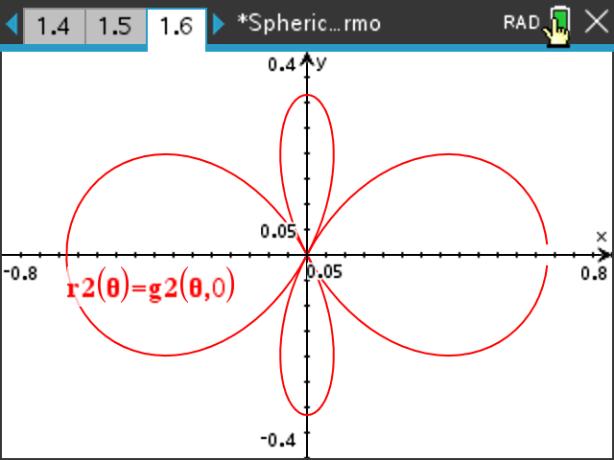
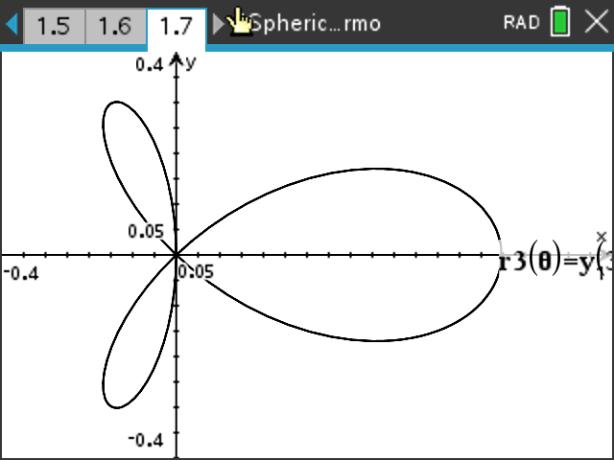
下図は,\(\small Y_1^0, Y_2^0\) のグラフです.
Nspireの「tns」ファイルは「こちら」に登録しました.関心を持たれた方は試してみてください.
TI-Nspireへの組込方は,
「37.3 Nspire本体との連携」の「Content Explorer」の箇所を見てください.
3DGraphでの媒介変数(参考:「17.4 曲面の媒介変数表示」)を利用することになります.

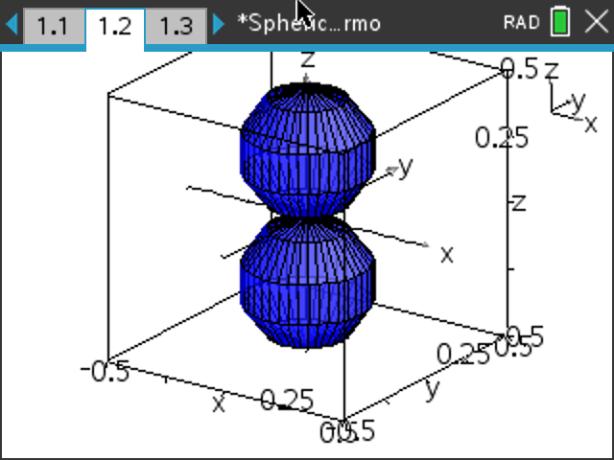
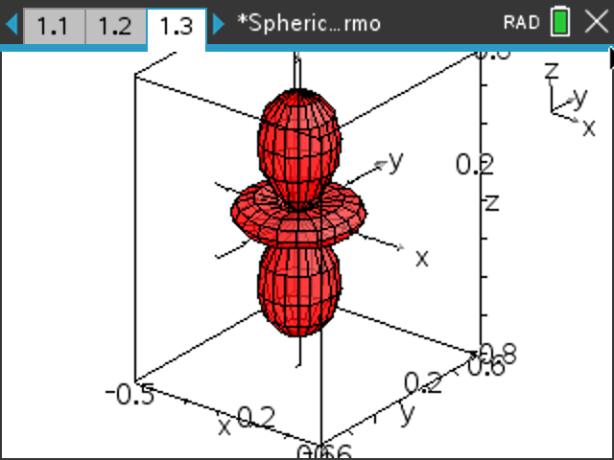
「TI-89Titanium」や「voyage200」には
曲面の媒介変数モードがないので曲面を描画することはできませんが,
TI-Nspireと同じ定義式で関数を定義して式を表示させることは可能です.
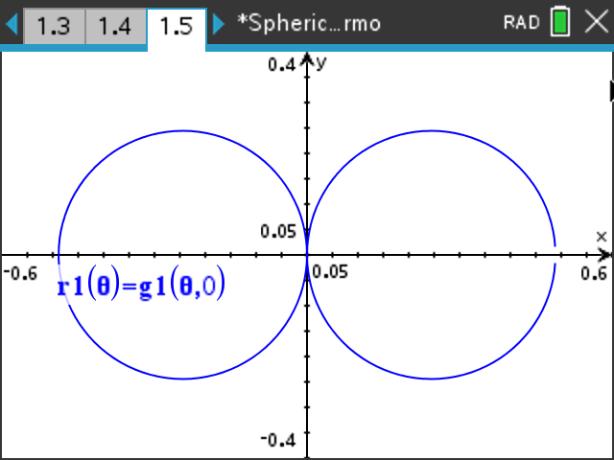
さらに,\(\small \theta, \phi\) のいずれかを固定すれば,
極座標での(平面)グラフを描画することができます.
それは,角を指定して断面図を描くことに相当します.
後半の3つの画面は,Nspireでなくても描画可能です.
- なお,この件に関する詳細は
Maximaでの解説を見てください.
★本書が,数学教育や工学教育でグラフ電卓の活用を考えるとき,
何かの参考になれば幸いです.
★全章をまとめたファイルを用意しました[PDF: 10MB]。
★ グラフ電卓が近くにないときは、数式処理ソフトをスマホやPCにインストールしておけば「いつでも・どこでも」グラフ電卓と同等の機能を利用することができます。
その機能を持つ無料のソフトとして「Maxima(マキシマ)」があります。その解説本を出版したので参考にしてください。
コマンドはAndroid版もPC版も同一なので、
iPhone所持の方はPC版のコマンドレファレンスとして利用することができます。
|








