■データの保存・読込
|
Maximaを統計解析で利用するには,まず解析すべきデータが必要です.
そのようなデータは「,」で区切って並べて [ ] で囲って表します.
このようなデータをリストといいます.
年度ごとの各種データは,
個々の年度のデータを列ベクトルとする行列で表します.
最初にサンプルデータを用意しましょう.たとえば,
気象庁による2016年の東京都の月ごとの平均気温を例に取り,
月を「month」,平均気温を「templ」とします.
| 月 | 1 | 2 | 3 | 4 |
| 気温 | 6.1 | 7.2 | 10.1 | 15.4 |
| 月 | 5 | 6 | 7 | 8 |
| 気温 | 20.2 | 22.4 | 25.4 | 27.1 |
| 月 | 9 | 10 | 11 | 12 |
| 気温 | 24.4 | 18.7 | 11.4 | 8.9 |
下図では,これらのデータをMaxima上で定義して,ファイル保存と読み取りを
行っています.
スマホ画面でも見やすい図とする都合上,
画面の右側は省略しています.(%i20)〜(%o33)の全体図は
こちらを参照してください.
以下は,(%i1)から始まっていません.
途中で入力違いがあったりしたときに最初からやり直すのは面倒なので,
半端な番号から始まっています.
途中で番号が飛んでいる箇所もありますが,
入力を間違えて上書きしたことによるものです.
いずれも,気にしないでください.
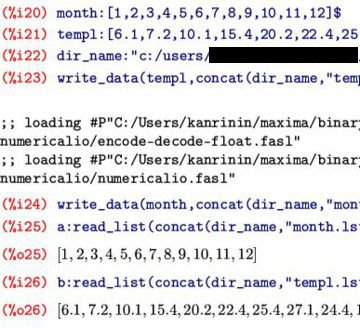
(%i20)では「month:[1,2,3,\(\small \cdots\),12]$」,
(%i21)では「templ:[6.1, 7.2, \(\small \cdots\), 8.9]$」と定義し,
それぞれ「$」により出力を抑制しています.
(%i22)では,このデータを保存するフォルダーを
「dir_name:"c:/users/(中略)/"$」により指定しています.
保存や読み込みを何度か行うことになりそうなときは,
あらかじめフォルダー名を適当な変数に割り当てておいた方がよいでしょう.
この後にファイル名を結合するので,最後は必ず「/」で終えます.
(%i23)では,データを保存するコマンド「write_data」を利用して,
「templ」のデータを保存しています.
書式は,「write_data(データ, 保存場所,'csv)」です.
第2引数では,文字列を結合するコマンド「concat」を利用して,
ファイル名をフォルダー名(dir_name)とファイル名(templ.lst)を
「concat(dir_name,"templ.lst")」により結合して表しています.
つまり,(%i23)では,templのデータを
「c:/users/(中略)/templ.lst」として保存したことになります.
第3引数「'csv」を付加すると「csv」形式(コンマ区切り)で保存されます.
これをつけないと,半角の空白で区切られて保存されます.
(%i24)では,月(month)について同様にしています.
(%i25)では,正しく保存されたことを確認するため,
保存ファイルを読み込んで「a」に割り当てています.
リストデータを読み込むには「read_list」を用いて
「read_list(ファイル名)」とします.
ファイル名は,
「concat」を利用してフォルダー名(dir_name)と
「month.lst」を結合したものです.
リストデータは,どんなに長いデータでも一つの行に保存されます.
複数の行を持つデータは行列データとして「read_matrix」で読み込む必要があります.

上図では,「month」と「templ」を行に持つ行列を,
同じ内容を持つ「a, b」を利用して「tokyo_kion」と定義し,
(%i23)と同様の書式で「kion.data」として保存しています.
そのデータは,2つの行をもつデータとして保存されます.
(%i29)では,複数の行を持つデータを読み込むために「read_matrix」を用います.
(%i29)を「read_list」により読み込むと,2つの行が繋がって1つのリストデータ
として読み込まれます.

行列の行や列は,それぞれ「row」「col」により取り出すことができます.
(%i30)では行列「c」の1行目を,(%i31)では3列目を,そして(%i32)では
(2,4)成分を取りだしています.
|
|
■いろいろな統計量
|
与えられた統計データから平均や分散等の基本統計量を求めるには,
統計関連の機能をまとめたパッケージ「descriptive」を読み込む必要があります.
このパッケージを利用すると,
下記のような統計量を求めることができます.
詳細は,マニュアルの
50.3節
を参照してください.
- <Maximaで求められる統計量>
- 平均、分散、不偏分散、標準偏差、最小値、最大値、範囲、
中央値、変動係数、平均偏差、p分位数、調和平均、幾何平均、歪度、尖度、各種のモーメント、相関係数、共分散行列、相関行列、主成分、等々
どのような出力が得られるかを確認する意味で,
文字変数のまま試してみましょう.

(%i40)では,統計パッケージ「descriptive」を読み込んでいます.
出力を抑制してもメッセージが表示されますが,気にしないことです.
最新版のMaximaでは,このメッセージは表示されません.
(%i41)ではリスト[x,y,z]を「dat」として割り当て,
(%i42)ではそのリストの長さ(length)を「nn」に割り当てています.
リストの個々の値は「dat[1], dat[2]」などで参照できます.
(%i43)では総和(sum)を,(%i44)では平均(mean)を求めています.
文字変数からなるリストなので,文字式で出力されます.
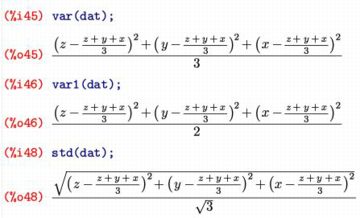
(%i45)では分散を求めています.出力された結果を見ると,
「平均との差の平方の平均」という分散の定義により計算されていることが分かります.
(%i46)は不偏分散,(%i48)は分散の平方根としての標準偏差です.
不偏分散の平方根は「std1」により求められます.
なお,周知のように,平均を \(\small \mu\) とすると,
分散は次の式で定義されます.
\[\small \displaystyle
\begin{align*}
(分散)~V^2&=\frac1{n}\sum_{k=1}^{n}(X_i-\mu)^2\\
(不偏分散)~U^2&=\frac1{n-1}\sum_{k=1}^{n}(X_i-\mu)^2
\end{align*}\]
次に,(%i21)で定義した東京都の気温(templ)で試してみましょう.

(%i49)は範囲(range),(%i50)は最小値(smin),そして(%i51)は最大値(smax)です.
(%i53)はメディアン(median)を求めています.
(%i55)はp分位数(quantile)を求めています.
ここでは2分位数を求めているのでメディアン(中央値)と一致します.
第3四分位数であれば「quantile(dat,3/4)」により求められます.
統計の教科書では四分位数しか触れられていませんが,
同じ書式で任意に指定する
p分位数 \(\small (0\lt p\lt 1)\) の値を求めることができます.
第3四分位数の場合は \(\small p=3/4=0.75\) です.
次に,行列データで考えてみましょう.

上図では,「dat2」を [u,v,w] とし,
行列「dat3」を(%i57)によりdatとdat2というリストを行に持つ行列とします.
この行列に対して平均(mean)を計算すると,
各列ごとの平均が(%o58)のようにリストで返されます.
つまり,行列データでは,列データに対して統計量が計算されます.
したがって,
リストで定義された幾つかのデータを行列にまとめて扱うときは,
個々のリストデータが列データになるようにする必要があります.
行と列を入れ替えるので,それは転置行列をとることで実現できます.
(%i59)では,dat3を転置(transpose)した行列をdat4としています.
そして,(%i60)でdat4の平均を求めています.
個々の列データの平均がリストで返されていることが分かります.
|
|
■いろいろなデータ処理
|
|
統計データに対しては,いろいろな統計量を計算したり,
様々な統計処理を行います.
Maximaの統計パッケージ「descriptive」を読み込むと
次のような処理を行うことができ,
新たにプログラムを組むことなく統計処理を行うことができます.
詳細は,マニュアルの
50.2節を参照してください.
- <Maximaでのデータ処理>
- 度数分布表の作成,
特定の条件を満たすデータの抽出,
指定した定義式によるデータ変換,
標準化変換
これらを試してみるには,少し大きなデータが必要です.
Maximaには3つのサンプルデータがあります.
- 「pidigits.data」:円周率 \(\small \pi\) の最初の100桁の数のリスト.
- 「wind.data」:アイルランドの5つの気象台で観測された日々の平均風速を
列とする (100,5) 型の行列.
- 「biomed.data」:異なるグループA,Bの患者の,
年齢と測定された4つの血圧を列とする (100,6) 型の行列.
離散データの処理
統計パッケージ「descriptive」は,すでに(%i40)で読み込まれています.
最初の例として,円周率の数のリストを読み込み「pidata」とします.
[shift][Enter]により改行して入力しています.
下図では,右半分は省略されています.
(%o45)により,「pidata」には円周率の数が読み込まれたことが分かります.
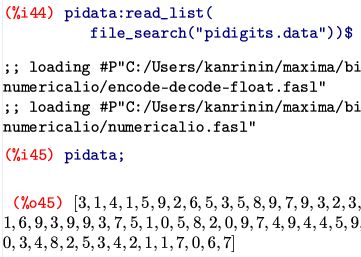
pidataは,0から9までの1桁の数からなるリストです.
最初に,これらの数が何個含まれているかを見てみましょう.
「continuous_freq(pidata, n)」により,
\(\small n\) 個に区分した度数分布を調べることができます.
第2引数のデフォルトは「10」に設定されているので,
10個に区分するのであれば省略できます.

「continuous_freq」を実行すると,上図のような結果が返されます.
右側部分は省略されていますが,(%o47)の後半には
[8,8,12,12,10,8,9,8,12,13]というリストが返されています.
前半の分数列のリストは,pidataをどのような階級に分けたかを表す
区分点のリストです.continuous_freqは,0〜9の数の度数を,
\(\small [0,\frac9{10}], [\frac9{10},\frac95],[\frac95,\frac{27}{10}],\ldots\)
という区間に分けて集計したことを示しています.
それぞれの区間には,\(\small 0, 1, 2, \ldots\) という整数しか存在しないので,
結果的に個々の整数が何個あるかを数え上げたことになります.
その個数のリストが後半の整数列からなるリストです.
(%i48)では,5区分の場合です.\(\small [0,\frac95], [\frac95,\frac{18}{5}],\ldots\) には,それぞれ2つずつの整数があります.後半の整数列は,
(%o47)の後半の整数列を2つずつ加えたものと一致しています.
連続データに対しても,同様の書式で度数分布を得ることができます.
「pidata」は離散データです.幾つかの区間に区分するのではなく,
異なるデータが単純に何個ずつあるかを知りたいときは
(%i49)のように「discrete_freq」を利用します.
この場合は,幾つかの区間に区分することはできません.
[0,1,2,...,9]という値が何個あるかが後半のリストで表されます.
|
|
連続データの処理
次に,連続データの場合を考えます.
Maximaには,サンプルデータとして
2つのグループに分けられた年齢と血圧の行列データ「biomed.data」があります.

(%i53)では,行列を読み取る「read_matrix」を利用して,
(%i44)と同様の書式で読み込んで「medata」に割り当てます.
(%i54)にあるように,100行からなるデータです.
(%i55)では,「medata[1]」により1行目を表示しています.
グループ名と年齢の後に4つの数値が並んでいます.
1行目だけ見ると最初の2つは最高血圧と最低血圧のように見えますが,
(%i56)で全体を表示させると,必ずしもそうではないように思えます.
マニュアルでは「4つの血圧」としか説明されていません.
medataは,1列目は計算のできないカテゴリカルデータです.
(%i56)で全体を眺めると,4列目と6列目には「NA」が含まれます.
「NA」は「no available」ということで,そこの値は無いことを示します.
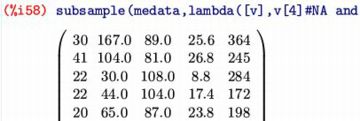
そこで,「subsample」というコマンドを用いて,
カテゴリカルデータやNAを含む行を除いてデータを作り直すことにします.
それは,次のような書式になります.
subsample(medata,
lambda([v], v[4]#NA and v[6]#NA),2,3,4,5,6)
書式は,「subsample(元データ,抽出基準, 抽出列)」という形です.
抽出基準ではラムダ関数(lambda)が使われています.この関数は「匿名関数」とも
呼ばれてMaximaでは重要な関数なのですが,ここで簡単に説明することはできません.
ともかく,上記のような書式で記述すると,4列目と6列目に「NA」を
含む行が除外された行列が返されます.
lambda( ) の括弧内の先頭にある [v] は,
vをローカル変数として使用することを宣言しています.
その後の式で,「4列目にNAを含まない,そして,6列目にも含まない」という
条件が記述されています.「#」は「\(\small \neq\)」を表します.
条件式の記述が長くなるときは,あらかじめ関数として定義しておくこともできます.
「g(x):=x[4]#NA and x[6]#AN$」
と定義しておいて,
「subsample(medata,g,2,3,4,5,6)」とすることもできます.
下図では,右半分は省略されています.
下図では,この行列を「medata2」に割り当てて,平均を計算したものです.
整数だけのデータの列では分数で表示されますが,
小数が含まれる列では小数で表示されます.右半分は省略されています.

一部の行を除外しないで,単純に1列目を除くだけであれば「transform_sample」
というコマンドを利用することもできます.
6列ある行列を5列にするには,下図の(%i69)のようにするだけです.
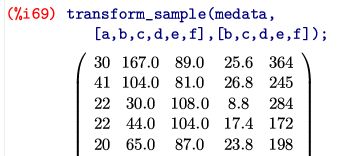
第2引数の [a,b,c,d,e,f] は,各列に名前をつけているだけです.
そして,第3引数で変換内容を記述しています.
この箇所で,列の順序を入れ替えたり,何らかの処理を施すことができます.
例えば,1列目を除くほかに,
2列目と3列目を交換,4列目は平方,
そして5列目と6列目を加えたものを6列目とするには,
第3引数を [c,b,d^2,e,e+f] とします.(結果の図は省略します.)
|
|
血圧の数値は連続データです.その度数分布は
「continuous_freq」を利用すると得られますが,
このコマンドの引数は行列ではなくリストである必要があります.
たとえば,medata2の2列目をリストに変換するには,
「list_matrix_entries」というコマンドを使用します.
1列からなる行列であればリストに変換されます.
複数の列をもつ行列であれば,行が繋がれて一つのリストで返されます.
簡単のため,「dat4」を
\[\small {\rm dat4}=\begin{pmatrix}x&u\\ y&v\\ z&w\end{pmatrix}\]
として試すと,下記のようになります.
なお,入出力の番号はずれています.

(%o66)のように,行列に対して適用すると,行が上から順に繋がって一つのリストに
なります.そこで,(%i67)では,dat4の2列目を「col(dat4,2)」により取り出して,
その列に対して「list_matrix_entries」を適用しています.
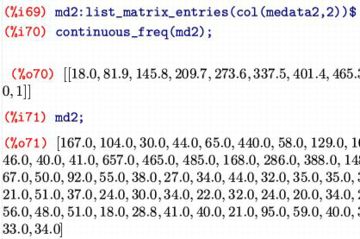
(%i69)では,medata2の2列目を「md2」に割り当てて,
(%i70)で度数分布を得ています.
第2引数を省略すると,デフォルトの10区分の度数分布が作成されます.
上図では右側が省略されていますが,下記の内容が表示されています.
(%o70) [[18.0,81.9,145.8,209.7,
273.6,337.5,401.4,465.3,529.2,
593.1,657.0],[73,7,3,1,2,1,2,1,
0,1]]
これは,\(\small [18.0, 81.9], [81,9, 145.8], \ldots\) の
区間に分割したときの度数が,それぞれ 73, 7, 3, \(\small \ldots\) であることを
示しています.md2の内容を表示させてみると,確かに81.9以下の値が大部分です.
デフォルトのまま作成すると,区間の左端と右端は最小値と最大値で設定されて,
その範囲(range)が10等分された小区間に分割されます.
実際,個々の区間幅は \(\small 81.9-18.0=63.9\) であり,
これは \(\small (657.0-18.0)/10=63.9\) の値と一致します.
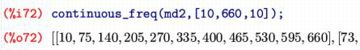
両端の値を切れの良い値とすることもできます.
たとえば,10〜660 の範囲で考えるには
「continuous_freq(md2,[10,660,10])」として,
第2引数に[左端, 右端, 区分数] を指定します.
次に,データが最初の小区間に集中しているので,その部分を細かく見てみましょう.
たとえば,100未満のデータを取り出して,10〜100を9分割してみます.

md2というリストから特定の条件を満たすリストを作成するコマンドは
「sublist」です.(%i73)では,
(%i58)のsubsampleと同様の書式でラムダ関数を利用して指定しています.
(%o74)では,下記の内容が表示されています.
20〜40の箇所に多くの値があります.
マニュアルには血圧のデータと書かれていますが,
何か違うデータなのではないでしょうか.
(%o74) [[10,20,30,40,50,60,
70,80,90,100],[3,26,21,8,10,
3,2,0,2]]
同様のことをmedata2の3列目を「md4」として行うと,下図のようになります.
md4では,度数が [1,6,10,12,16,14,13,5,8,6] となり中央が大きくなっていて
普通の分布(?)のように見えます.

(%o76) [[59.4,64.61,69.82,75.03,
80.24,85.45,90.66,95.87,101.08,
106.29,111.5],[1,6,10,12,16,14,
13,5,8,6]]
コマンド「standardize」を利用すると,データの標準化を行うこともできます.
標準化は,平均を \(\small \bar{X}\),標準偏差を \(\small \sigma\) とするとき,
\[\small Z=\frac{X-\bar{X}}{\sigma}\]
により定義される値です.
引数は,リストか行列です.
行列を引数にすると,各列の平均と標準偏差をもとにして標準化が行われます.

上図では,リスト「md4」を引数としています.
(%i87)では,md4の最初の値を標準化しています.
(%o88)で表示されるとリストの最初の値と一致していることが分かります.
また,下図のように,平均は \(\small 0\),標準偏差は \(\small 1\)
になっています.

|
|
■統計グラフ
統計パッケージ「descriptive」を読み込むと,
折れ線グラフ以外のいろいろな統計グラフを描画することができます.
詳細は,マニュアルの50.4節を参照してください.
|
|
折れ線グラフ
離散データの場合は,どの値がどの程度あるのかを把握する必要があります.
結果の集計は「descrete_freq」により得られますが,
そのグラフ化に「plot2d」を利用することができます.
「plot2d」は連続関数のグラフばかりではなく,
このような離散データのグラフも描画することができます.書式は,
\(\small x\) 座標のリストをLx,
それに対応する \(\small y\) 座標のリストをLyとするとき,
「plot2d([discrete, Lx, Ly])」により対応する点を線で結んだ
グラフが描画されます.Lxは小さい順に並んでいる必要があります.
「pidata」を例にして折れ線グラフを描画してみましょう.
下記では,Lxを「Lx: makelist(i,i,0,9)」により割り当てています.
「makelist(式, 変数, 初期値, 終了値)」により,式で定められた値のリストが
生成されます.直接「Lx: [0,1,2,\(\small \cdots\),9]」とすることもできます.
Lyは,(%o72)の2番目のリストとして割り当てています.
(%i77)で \(\small y\) の範囲を指定しないと,
最小値と最大値の間のグラフが描画されます.
なお,「TeXmacs+Maxima」の場合は,[Enter]で実行,[shift][Enter]で改行します.
wxMaximaの場合は[shift][Enter]で実行,[Enter]で改行するので注意してください.

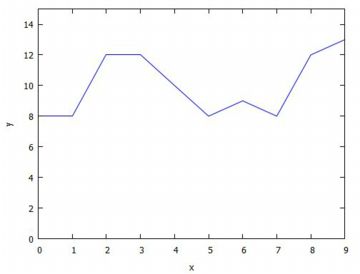
グラフはデフォルトでは実線で結ばれますが,
点線で結んだり点を配置するだけにすることもできます.
描画のスタイルは [style, 線種] により指定します.
デフォルトでは「lines」が指定されています.
点線とするには「dots」,孤立点とするのは「points」,
実線で結んで点を打つには「linespoints」とします.
下図では「linespoints」を指定しています.

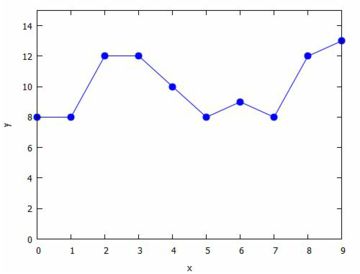
点のタイプは,「point_typle」により指定することができます.
指定できるタイプは下記のものです.
-
bullet(\(\small \bullet\)), circle(\(\small \circ\)) , plus(\(\small +\)),
times(\(\small \times\)), asterisk(\(\small *\)), box(■), square(\(\small \square\)), triangle(\(\small \triangle\)), delta(\(\small \Delta\)),
wedge(\(\small \wedge\)), nabla(\(\small \nabla\)), diamond(\(\small \diamond\)), lozenge(\(\small \lozenge\))
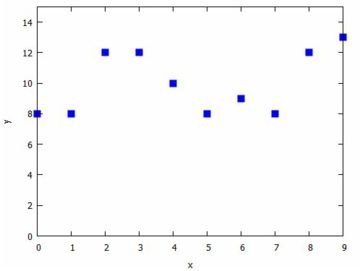
下記では,孤立点を配置するようにして,点のタイプには「box」を指定しています.
ただし,Maximaのバージョンによっては,上記の全てが利用できるとは限りません.
このページでは,「TeXmacs+Maxima」の画面を紹介していますが,
そこで使用されているMaximaのバージョンは「5.38.1」です.このバージョンでは
「box」は利用できませんでした.
下図は,Maxima5.42.2が利用されているwxMaximaの画面です.

以上の例ではデータの \(\small x\) 座標が小さい順に並んでいますが,
取得するデータの種類によっては大小がばらばらの状態でデータが得られるかも
しれません.そのようなときは,個々の点の座標を指定して同様のグラフを描画
することができます.
たとえば,「pidata」の度数分布は次のようになっています.
| 数 |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
7 | 8 | 9 |
| 度数 |
8 | 8 | 12 | 12 | 10 | 8 | 9 |
8 | 12 | 13 |
ここで,順番をばらばらにして,個々の点の座標からなるリストとして,
Lxyを次のように定めます.
Lxy:[[5,8],[0,8],[6,9],[1,8],[7,8],[2,12],[8,12],[3,12],[9,13],[4,10]]$
その上で,「plot2d([discrete,Lxy],[y,0,15],[style,points],[point_type,box])$」
としても,上記と同じ図が得られます.
ただし,「style」に「points」以外を指定すると,
Lxyに並んだ順に線で結ばれることになるので注意してください.
下図は,[style,linespoints] と [point_type, circle] を指定した場合です.
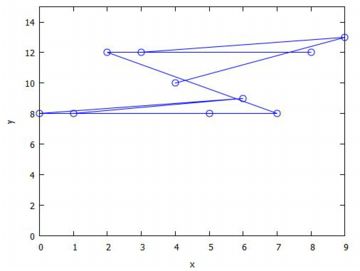
|
|
棒グラフ (barplot)
離散データの場合は,どの値がどの程度あるのかを把握する必要があります.
結果の集計は「descrete_freq」により得られますが,
それを棒グラフで表すには「barsplot」を利用します.
(%i44)
で円周率100桁の値のデータ「pidigits.data」を
「pidata」に割り当てているので,それを利用します.
単純に「barsplot(pidata)$」とすると,
下図が表示されます.引数はリストや行列です.
どのような数が何個あるかが棒グラフで表示されます.
「gnuplot」を用いて描画されています.
軸のスケールを変えたり,棒の色を変えて塗りつぶすこともできます.
縦軸はデフォルトでは度数で表示されます.
相対度数にするには,
「barsplot(pidata,[frequency=relative]) とします.
度数は「absolute」,百分率は「percent」で指定します.
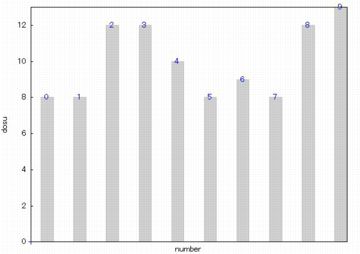
上図は,下図の(%i92)のコマンドで描画されています.
「fill_density」は,棒を塗りつぶすときの濃さを0〜1の間の数で指定します.

グラフ描画を行う別なコマンド「draw」を利用すると,
さらに細かい指定を行うこともできます.
ただし,コマンド「draw」は機能が豊富すぎて簡単には説明できません.
詳細は,マニュアルの53節にある「53.2.3 Graphic options」を参照してください.
|
|
ヒストグラム (histogram)
リストか1次元行列にまとめられたデータから
ヒストグラムを作成するには「histogram」を利用します.
円周率のデータ「pidata」を与えて「histogram(pidata)$」とすると,
下図が表示されます.
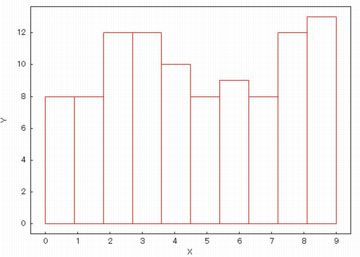
棒グラフと同じですが,柱は隙間無く隣り合わせになっています.
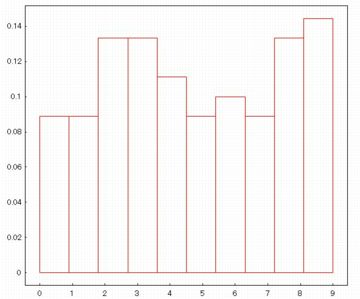
縦軸は度数になっていますが,下図にある(%i94)のように
「frequency=density」を追加すると確率密度になり
柱の面積が相対度数になります.この場合,
全面積は \(\small 1\) です.
「density」の他に,「absolute」「relative」「percent」が
指定できます.デフォルトは「absolute」になっていて度数になります.
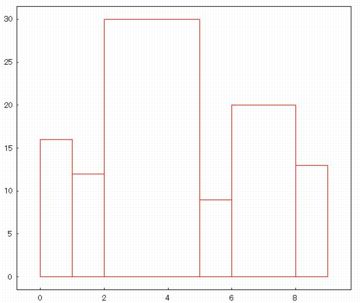
「いろいろなデータ処理」の箇所で述べた
「continuous_freq」や「discrete_freq」を利用すると,
度数分布の区分は等分になりますが,ヒストグラムでは
「nclasses」というオプション変数を利用すると,
区分点を不均等に指定することができます.
(%i95)では,nclassesに区分点の左端を指定しています.
「nclasses=5」のようにすると,5等分して表示されます.
ただし,
(%i95)のような区分点の指定は,
「TeXmacs+Maxima」ではエラーになりました.下図は,
Maxima5.42.2が組み込まれているwxMaxima(19.01.2x)によるものです.
区分点の指定機能はMaxima5.38.1以降に追加された機能のようです.
棒グラフの場合と同様に,
「draw」を利用するとさらに細かい指定を
することができ,確率密度曲線を重ね合わせることもできます.

|
|
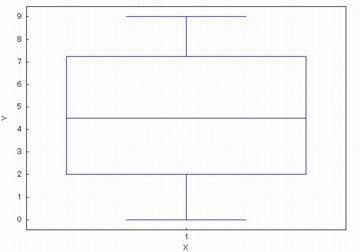
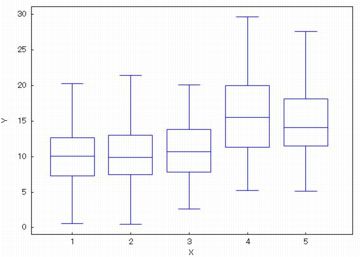
箱ひげ図 (boxplot)
箱ひげ図には中央値,四分位数,最小値,最大値などの情報が図示されるので,
データの全体像を把握するときによく利用されます.
「boxplot」により描画することができます.引数は,リストか行列です.
下図は,「boxplot(pidata)$」とした場合の図です.
箱の横幅が広すぎるときは,「box_width」の値で調整することができます.
0〜1 の間の値で指定します.
下図は,(%i97)にあるように「box_width=0.2」としています.

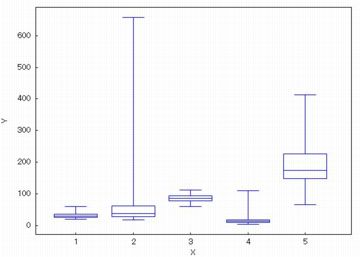
引数が行列のときは,各列の箱ひげ図が図示されます.
下図は,(%i59)で定義した「medata2」の場合です.
2列目には異常値が含まれていることが分かります.
おそらくは,小数点のつけ損ないによるものではないでしょうか.
だとすると,この箱ひげ図からは,
2列目は最小血圧,3列目は最大血圧のデータのように思えます.

|
|
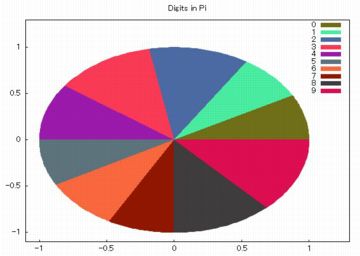
円グラフ (piechart)
円グラフを描画するには「piechart」を用います.
引数には,リストか,行列の一つの行または列を取ることができます.
下図は,「piechart(pidata)$」の図です.
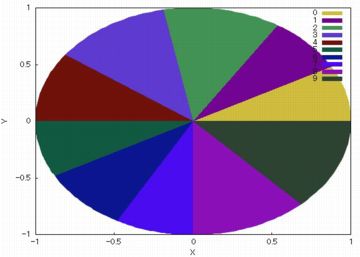
図が枠内で大きすぎるときは,縦と横の範囲を xrange, yrange を利用して
調整するか,または円の半径を 「pit_radius=a」により指定します.
デフォルトの半径は \(\small 1\) です.
カラーチャートは描画する度に自動的に変更されます.
自分で指定するには,色のリストを 「sector_colors」に指定します.

|
|
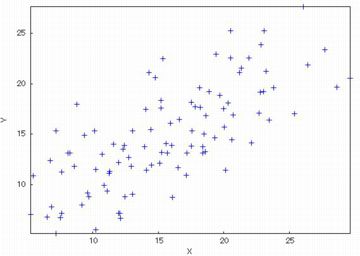
散布図 (scatterplot)
2変量の間の関係を見るには,散布図を描いてみるのが有効です.
散布図は「scatterplot」により描画することができます.
箱ひげ図をみると,
データとして血圧のデータ (medata) は相互関係を見るのに適さないので,
風速のデータ (wind.data) を利用することにします.
以下では入出力番号をリセットしたので,パッケージ「descriptive」を
読み込むところから始めることにします.
そして,(%i2)により風速のデータを「wind」に割り当てます.

「wind」は(100,5)型の行列です.(%i3)では各列の平均を見ています.
(%i4)により箱ひげ図を描画してみて,
その状況から4番目と5番目のデータの散布図を見ることにしましょう.

下図は,(%i4)による,5箇所の気象台の風速データの箱ひげ図です.
scatterplotに5列からなる行列「wind」の2つの列を引き渡すために,
「submatrix」を利用します.
このコマンドの書式は,たとえば
「submatrix(i1,i2,行列データ,j1,j2,j3)」とすると,
行列データから \(\small i_1, i_2\) 行と,\(\small j_1, j_2, j_3\) 列を
除いた行列が返されます. \(\small i_1, i_2\) を省略すると後半の列だけが除かれ,
\(\small j_1, j_2, j_3\) を省略すると前半の行だけが除かれます.
そこで,上図にある(%i5)により,1〜3列を除いた行列を「wind45」とします.
散布図は,(%i7)により次のように描画されます.
散布する点のタイプは,「point_type」
により変更することができます.
(%i8)のように「circle」を指定すると下図が描画されます.
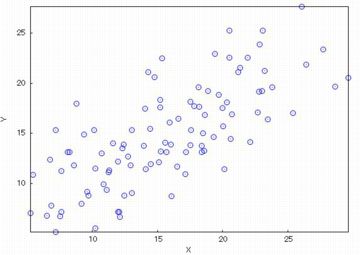
なお,Maximaの古いバージョンでは,「point_type」のタイプによっては
エラーになる場合があるので注意してください.
その場合は,最新版のMaximaを利用すべきです.
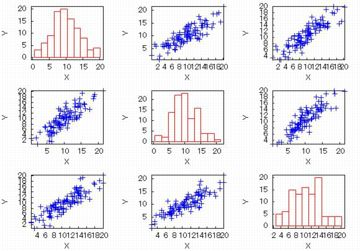
2つの列に限定しないで引き渡すと,相互の列どおしの散布図が一気に作成されます.
たとえば,(%i9)のように4列と5列を除いた行列を引き渡すと,
下図のように各列の相互関係が行列形式でまとめて表示されます.
画面の拡大図は,こちらを参照してください.
|
|
確率密度曲線
ヒストグラム「histogram」は
他のグラフと重ね合わせることができませんが,
「draw」パッケージを利用すると,
ヒストグラムに
確率密度曲線を重ね描きすることができます.
詳しくは「確率分布」の箇所で
解説しますが,
Maximaでは20以上の確率分布を扱うことができ,それぞれの分布について
確率密度関数や分布関数が登録されています.
また,その確率分布にしたがう乱数も
発生させることができます.
ヒストグラム作成の元になるリストデータを alist,
確率密度関数を f(x) とすると,
次の書式で2つのグラフを重ね合わせることができます.
draw2d(
histogram_description(
alist, frequency=density),
explicit(f(x), x, a, b),
xrange=[c, d], yrange=[e, f])$
ここでは,3つのパッケージ「distrib」「descriptive」「draw」
を読み込み済みとします.
「histogram_description」は,
drawパッケージの中でヒストグラムを利用したい場合のコマンドです.
データリストを指定した後で,「frequency」や「nclasses」の指定を
することができます.
「explicit」は,drawパッケージの中で
陽関数 (\(\small y=f(x)\) のタイプの関数)を扱うときのコマンドです.
その関数のグラフを描画する範囲も指定します.
xrange と yrange により,
2つのグラフを納める外枠の大きさを指定することができます.

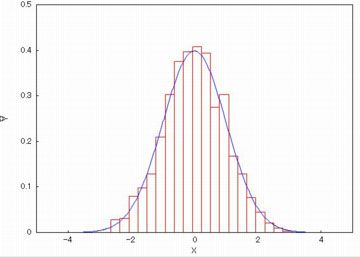
(%i5)の「histogram_description」では,
標準正規分布にしたがう乱数(random_normal)からなる
大きさ1000のリストのヒストグラムを,
縦軸を確率密度(density)にして20階級で描画するように指定しています.
「explicit」の箇所では,N(0,1)の確率密度関数「pdf_normal(x,0,1)」の
グラフを区間 \(\small [-5,5]\) の範囲で描画するように指定しています.
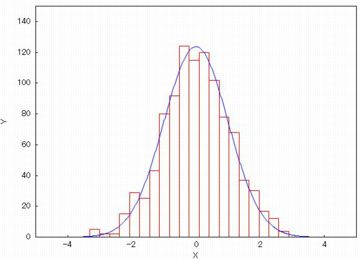
ヒストグラムは度数を表示しません.
縦軸を度数にするには「frequency」に「absolute」を指定します.
しかし,それがデフォルトの設定なので,
「frequency」を指定しなければ縦軸は自動的に度数で表示されます.
それに確率密度曲線を同時に表示させるため,
度数のグラフからヒストグラムを得るときの逆の計算を行い,
確率密度関数にリストの大きさと階級幅を掛けます.

(%i11)では,いったん発生させた乱数のリストを「alist」に
割り当てて,その範囲(最大値\(\small -\)最小値)を(%i12)で求めています.
(%i13)で20階級に分けたときの階級幅は「haba/20」になります.
(%i13)の中で「random_normal」が何度も呼び出されると,
その度に新たな乱数が発生して範囲も異なることになるので,
ここでは(%i11)で発生させた乱数のリストを固定して考えています.
グラフは下図のようになり,縦軸が度数になっています.
|
|
|
■いろいろな乱数
|
|
統計の学習では,「サイコロを100回振る」などを
自分で試してみることも必要ですが,実際にやるのは面倒です.
そのようなときは「乱数」を利用するとよいでしょう.
Maximaはいろいろな確率分布にしたがう乱数を発生させることができます.
詳細は,マニュアルの「52. distrib」を参照してください.
ここでは,疑似乱数,二項乱数,正規乱数についてのみ解説します.
この項目を試すには,確率分布に関するパッケージ「distrib」を
読み込む必要があります.
- <Maximaが乱数を発生させられる確率分布>
- 離散分布
- 一様分布,二項分布,負の二項分布,ポアソン分布,ベルヌーイ分布,幾何分布,超幾何分布,等々
- 連続分布
- 一様分布,正規分布,t 分布,カイ二乗分布,
F 分布,指数分布,対数分布,ガンマ分布,ベータ分布,
ロジスティック分布,パレート分布,ワイブル分布,レイリー分布,ラプラス分布,
コーシー分布,ガンベル分布
|
疑似乱数 (random)
引数 x に対して「random(x)」は,
x が正の整数のときは 0 から x-1 までの整数を,
正の浮動小数点のときは x よりも小さい非負の浮動小数点を返します.
「random」はデフォルトの機能なので,パッケージを読み込む必要はありあません.

上図では,引数が整数,浮動小数点,負の整数の場合です.
値が1個だけ返されます.この後に同じコマンドを実行すると,
新たな乱数が返されます.結果が同じとは限りません.
「乱数」とはいっても,何らかの数学的性質に基づいて計算された値が返されます.
その意味で疑似乱数といいます.
乱数発生のアルゴリズムには,日本の松本眞・西村択士により考案された
メルセンヌ・ツイスター
という方式(MT19937)が用いられています.
これを用いて,たとえばサイコロを15回振ったときの数をシミュレートするには,
「random(6)」を15回実行します.
0〜5の値が返されるので,その値に 1 を加えることで1〜6の値が得られます.
実際には,個別に行うのではなく,
(%i6)や(%i7)のように「makelist」を利用して15個の要素を持つリストを作成します.
(%i7)は(%i6)に 1 を加えているわけではなく,
新たに発生した乱数に 1 を加えたものです.

どの目が出る確率も同じようになっていることを確認するため,
振る回数を増やしてみます.
または,たとえば「dice(n)」を
「makelist(random(6)+1,i,1,n)$」により定めて,
dice(100)などで参照することもできます.

上図では,それぞれ百回,千回,1万回のリストを生成しています.
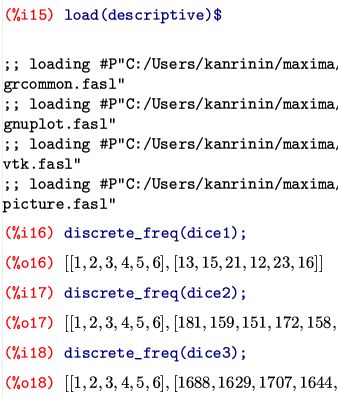
このようなときは,末尾を「$」として出力を抑制しておきます.
下図では,それぞれの度数分布 (discrete_freq)
を求めています.
そのコマンドはパッケージ「descriptive」に含まれているので,
最初にそれを読み込んでいます.
なお,出力の右側は省略されています.
これをグラフ化してみましょう.
「plot2d」を利用した折れ線グラフを作成するため,
最初に \(\small x\) 座標と \(\small y\) 座標のリストを
下図の(%i19)〜(%i22)のように定めます.
離散データのグラフを描画する「plot2d」の書式では
[discrete, x座標のリスト, y座標のリスト] を入力することになります.
記述が長いので,
それぞれ(%i23)〜(%i25)のようにあらかじめ割り当てておきます.
リストの長さ(length)で割って相互比較ができるようにしています.

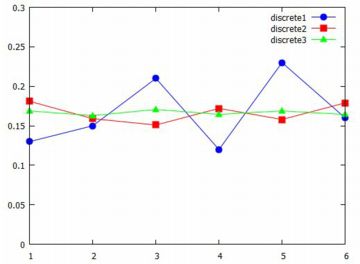
以上の準備のもとで,それぞれの折れ線グラフは次のように描画されます.
それぞれは \(\small 1/6=0.166\cdots\) に近づくはずなので,
\(\small y\) 軸の範囲は \(\small [0, 0.3]\) としています.
描画のタイルは「linespoints」を指定して,点を打つようにしました.
色や点の記号は自動的に割り振られます.
回数が増えるほど,一定値に近づいていくことが見て取れます.
このように,どの値の出る確率も同じなのが一様分布です.
次に,浮動小数点で同様のことを確かめてみましょう.
下図の(%i27)(%i28)では,「random(1.0)」により0〜1の浮動小数点の
リストを作成しています.(%i29)(%i30)では,
連続データの場合の度数分布 (continuous_freq)
を求めています.
第2引数の [0,1,10] は,
両端に0と1を持つようにして10区分するようにしています.
この指定をしないと,出力される区分点は半端な浮動小数点で表示されます.

(%o30)の1番目のリストは,11個の値を持ち2番目のリストと個数が合いません.
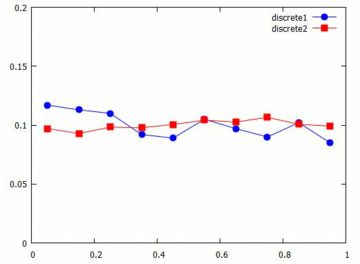
そこで,(%i31)では,0.1刻みで10個の値を持つリストを作成しています.
Ly1, Ly2の値が階級の中央にくるようにするため,(%i34)(%i35)では
\(\small x\) 座標を 0.05 だけずらしてます.

以上により,下図のグラフが描画されます.
1千回と1万回だけの比較ですが,乱数の発生回数が大きいほど一定値の 0.1 に
近づいていることが分かります.
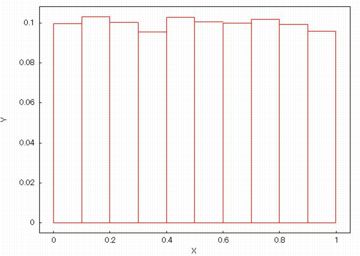
上記は,2つのグラフの比較をするために折れ線グラフで示しましたが,
一つのリストの分布を見るだけであれば「histogram」が
利用できます.下図は,
histogram(float2,frequency=relative)
とした場合です.
「float2」が呼び出されるたびに新たな乱数が発生するので,
図を表示させるごとに異なるグラフになります.
上記の折れ線グラフをヒストグラムにしたわけではありません.
|
|
乱数の種(シード) (random_state)
いろいろなシミュレーションをするとき,
乱数生成器に同じ乱数を発生させたいときがあるかもしれません.
乱数は,「乱数の種(シード)」と呼ばれる一つの数をもとにして
生成されます.
その値を,Maximaでは「ランダム・ステート (random_state)」と呼んでおり,
それを操作する関数として「make_random_state」と「set_random_state」があります.
「make_random_state」は次のような機能を持っています.
いずれも,「ランダム・ステート」を新たに作成したり,表示したりするだけです.
乱数生成器の状態に変化はありません.
- make_random_state(n):整数 n (負でもよい) を
\(\small 2^{32}\) で割った値をもとに新たなランダム・ステートを作成する.
- make_random_state(S):「S」にランダム・ステートが割り当てられているとき,
その値を表示する.
- make_random_state(true):PCの現在時刻をもとに
新たなランダム・ステートを作成する.
- make_random_state(false):乱数発生器の
現在のランダム・ステートの状況を返す.
乱数発生器のランダム・ステートの値を変更するには
「set_random_sate」を利用します.
「S」にランダム・ステートが割り当てられているとき,
「set_random_sate(S)」により乱数生成器の状態を変更することができます.
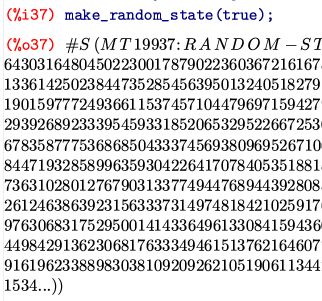
(%i37)では,「make_random_state(true)」として,PCの現在時刻をもとにして
新たなランダム・ステートを生成しています.右側は省略されていますが,
かなりの桁数の整数が表示されます.これが,「ランダム・ステート」です.
新たに生成されただけであり,乱数発生器にコピーされたわけではありません.

(%i38)では,引数を「false」にして,現在のランダム・ステートを
「S」に割り当てています.
その後で2つの乱数を発生させています.
なお,「S」を表示させると,(%o37)とは異なる結果が返されます.

(%i41)では,(%i38)で割り当てたランダム・ステートの値を
乱数発生器にコピーして,もう一度2つの乱数を発生させています.
同じ乱数が返されていることが分かります.このように,
同じ乱数を繰り返したいときは,乱数を発生させる前に
「ランダム・ステート」の値を取り出して保存しておくことが必要です.
その値を「set_random_state」を利用してコピーすれば,
同じ乱数を発生させることができます.

(%i45)では,2つの乱数を発生させた後のランダム・ステートの状態を「S2」に
割り当てて,「S」と「S2」は一致するかどうかを調べています.
「is」は真偽を判定するコマンドです.
等式,不等式,論理式の真偽を判定することができます.
「false」が返されるので,「S=S2」は「偽」です.
つまり,2つの乱数を乱数を発生させる前のランダム・ステートと,
発生させた後のランダム・ステートは異なることが分かります。
|
|
二項乱数 (random_binomial)
二項分布Binom(n,p)は,ある試行で事象Aの起きる確率を \(\small p\) とするとき,
その試行を \(\small n\) 回繰り返して事象Aが何回起きたかを表す分布です.
たとえば,「サイコロを100回振って1の目が何回出たか?」という数は二項分布に
したがいます.「random_binomial(n,p)」は,この二項分布にしたがう乱数を
1個返します.「random_binomial(n,p,m)」とすると,
m個からなるリストを返します.
前の項目の疑似乱数「random」はデフォルトの機能ですが,
二項分布にしたがう乱数を発生させるには確率分布に関するパッケージ「distrb」を
読み込む必要があります.また,発生させた後の度数分布を調べるために,
統計パッケージ「descriptive」も読み込んでおきます.
2つのパッケージを読み込んだ上で,下記の(%i3)は
「サイコロを10回振って1の目の出た回数」を表す二項乱数を,
「10回振る」という操作を15回行った場合のリストとして発生させています.

この乱数を利用していろいろ試してみるには,
コマンドを入力するのが面倒です.そこで,
「sampbin(n)」を下図の(%i4)のように定めます.
これにより,大きさ \(\small n\) の二項乱数のリストが生成されます.
(%i6)は100回行った場合,
(%i7)は1000回行った場合の度数分布を表示しています.
この結果を見ると,
確率 1/6 では10回振る中でせいぜい5回出れば関の山といえそうです.
(%o7)をみると,10回振る操作を1000回行ったのに,
この場合では6回も出たことが1度も無かったことを示しています.

次に,この度数分布のグラフを表示してみましょう.
plot2dで離散データを表示するには,[discrite, xのリスト, yのリスト]
で指定する必要があります.
(%i8)では,(%o7)の最初のリストを Lx にしています.
(%i12)では y のリストを定義していますが,右側が切れています.
次のように定義しています.
Ly(n):=discrete_freq(sampbin(n))[2]/length(sampbin(n))$
度数のリストは,度数分布(discrete_freq)の2番目のリストで返されます.
それを取り出して,元データである乱数リスト(sampbin(n))の大きさ(length)で
割って基準化しています.
その上で,下図の(%i13)のように定めておきます.

以上のように定めた上で,表示するグラフの \(\small x, y\) の範囲や
描画スタイルを(%i15)のように定めるとグラフが描画されます.
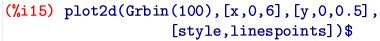
ただし,ここでは,Lxを [0,1,2,3,4,5] としているので,
sampbin(n)に6回出た場合が含まれると Lx と Ly の成分の個数が合わないので,
plot2dでエラーが生じます.
そのエラーを回避するには,Lxは0〜6として,
Lyに6回出た場合の度数が含まれない場合は
Lyの最後に0を追加するように定める必要があります.
しかし,それを記述するにはMaximaのプログラミングが必要になります.
plot2dを実行するごとにsampbin(n)により新たな乱数リストが作成されるので,
何度かやっていると6回が出ないケースになってグラフが描画されるでしょう.
nをもっと大きな数で試したい場合は,Lxは0〜6にしておくのがよいでしょう.
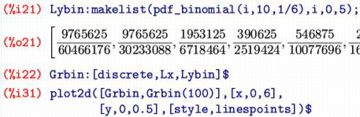
二項分布の確率を表す関数と重ね合わせることもできます.
その確率を表す関数は「pdf_binomial(x,n,p)」であり,次の式で定義されます.
\[\small \binom{n}{x}p^x(1-p)^{n-x}\]
この関数は,\(\small x\) は 0〜n の整数のときだけ値を持ち,
それ以外の値のときは 0 が返されます.なお,
plot2dで描画するたびに新たに発生させた乱数によるグラフが描画されるので,
(%i15)によるグラフとは一致しません.
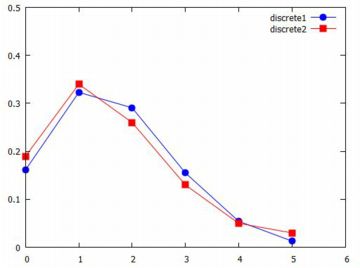
下図では,青のグラフが二項分布です.Grbin(n)の n を増やしていくと,
この青いグラフに近づいていきます.
なお,書式に誤りがないのにplot2dでエラーが出るときは,何度か試してください.
n をもっと大きな値で試すときは,6回出た場合も含まれるように,
Lx, Ly, Lybinは作り直す必要があります.
|
|
正規乱数 (random_normal)
正規分布は,いろいろな場面で現れる重要な確率分布です.
平均 \(\small m\),標準偏差 \(\small s\) の正規分布にしたがう乱数は
「random_normal(m,s)」により得られます.
\(\small n\) 個の正規乱数を成分を持つリストを得るには
「random_normal(m,s,n)」とします.
この乱数を利用するには,パッケージ「distrib」が必要です.
なお,正規乱数を発生させるアルゴリズムには
ボックス=ミューラー法が用いられています.

上図は,すでに「distrib」と「descriptive」を読込済みとして,
(%i32)では \(\small m=0, s=1\) の正規乱数を1個得ています.
(%i33)では \(\small m=50, s=10\) の正規乱数を12個得て,
「truncate」により小数部分を切り捨てて整数のリストを得ています.
次に,二項乱数と同様にして,発生させた正規乱数の度数分布を作成して
グラフにしてみましょう.
下図の(%i41)では, \(\small m=0, s=1\) の正規乱数の \(\small n\) 個の
リストをsampnorm(n)としています.
(%i42)では,そのリストデータの
区間 \(\small [-3, 3]\) を12等分した場合の
度数分布を作成してnormdosu(n)としています.
「continuous_freq」を利用すると,
連続データの度数分布を作成することができます.
第2引数の [-3, 3, 12] は,区分点の両端を \(\small -3, 3\) にして,
その区間を12等分するように指定するためのものです.
小区間の幅は 6/12=1/2=0.5 となります.
区間を指定しないと,sampnorm(n)の最小値と最大値の間が12等分されて,
両端や区分点が半端な数値になります.
(%i46)では,\(\small n=100\) の場合の度数分布を出力させています.
(%i45)の最後で [2] を指定することにより,この分布が得られます.
[2] を指定しないと,区分点のリストと度数分布のリストが得られます.
(%i47)では,度数に対応する \(\small x\) 軸の区分点のリストを作成しています.
そのリストは,(%i45)の最後を [1] に指定しても得られますが,
12個の度数分布得るには13個の分割点が必要です.[1] を指定して利用すると,
plot2dでグラフを描くときに個数が合わずにエラーが生じるので,
度数分布の値と個数が合うようなリストを作成しておきます.
度数の値が個々の階級の中央にくるように 0.25 だけずらしています.
(%i48)は,記述が長くなるので,plot2d 第1引数を事前に指定しています.

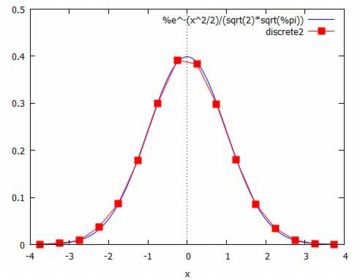
以上のもとで,グラフは下図のように描かれます.
度数をリストの大きさ(length)で割っているので,縦軸は相対度数になります.
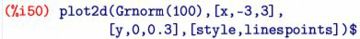
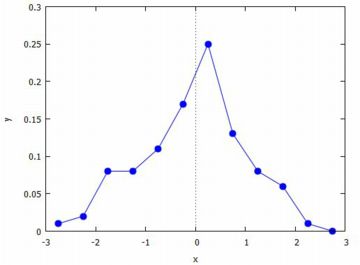
このグラフは,標準正規分布 \(\small N(0,1)\) のグラフに近づいて
いくはずです.そのことを確かめてみましょう.
正規分布 N(m,s) の確率密度関数は「pdf_normal(x,m,s)」です.
周知のように,この関数は次の式で定義されます.
\[\small \frac1{\sqrt{2\pi}s}e^{-\frac{(x-m)^2}{2s^2}}\]
確率密度関数は,柱の面積が相対度数になるようなものなので,
縦軸を相対度数で定めている(%i48)の定義ではちょっと不具合が生じます.
\(\small (面積)=(階級幅)\times(縦)=(相対度数)\)
となるようにする必要があるので,
(%i51)のように階級幅で割った式で定義し直しておきます.
その上で,(%i52)により下図のグラフが描画されます.

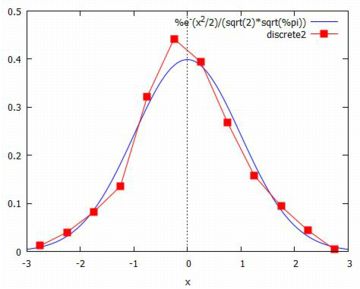
ただし,「TeXmacs+Maxima」では,(%i52)ではエラーが生じました.
このグラフは,wxMaximaで描画したものです.
エラー原因は,おそらく(%i45)での [-3,3,12] という指定にあると思われ,
[-3, 3] の範囲を超えた値に対応できなかったことによると思われます.
Maximaの最新バージョン(5.42.2)が組み込まれているwxMaxima(19.01.2x)で試すと,
範囲指定をして得られた度数の合計は,指定した n にはなっていませんでした.
指定した範囲内の数の度数を集計するように修正されているようです.
「Maxima」は世界中のボランティアにより保守されており,
このような不具合が修正されたり新しい機能が追加されたりして
新しいバージョンになっていきます.
「TeXmacs+Maxima」で記述は合っているはずなのに「エラー」が生じるときは,
最新版のMaximaでやり直してみるとよいでしょう.
「TeXmacs+Maxima」で上記のエラーが生じないようにするためには,
指定する範囲と区分点の個数を変更します.
たとえば,[-4,4,16] として,
(%i47)は「Lx:makelist(-4.25+0.5\(\small *\)i,i,1,16)」
とすればよいと思われます.下図は,
\(\small n=10,000\) の場合の「TeXmacs+Maxima」の画面です.
それでもエラーになるときは,範囲と区分点をさらに修正すれば良いと
思われます.

|
|
逆関数法による乱数の発生
Maximaに登録されている乱数の他に,
いろいろな確率分布にしたがう乱数を自分で発生させることができます.
具体的には,次の手順でその確率分布にしたがう乱数が発生します.
- 乱数を発生させたい確率分布の累積分布関数を求める.
- 累積分布関数の逆関数を求める.
- 区間 \(\small [0,1]\) における一様乱数の,
逆関数による値を求める.
- 上記の値が,想定した確率分布にしたがう乱数です.
上記の値が想定する確率分布にしたがうのは,以下の理由によります.
今,ある連続的な確率分布にしたがう確率変数を \(\small X\) として,
その累積分布関数を \(\small F(x)\) とします.
つまり,確率密度関数を \(\small \varphi(x)\) として,
\[\small F(x)=\int_{-\infty}^{x}\varphi(t)\,dt=P(X\leq x)\]
とします.\(\small 0\leq F(x)\leq 1\) であり,
\(\small y=F(x)\) が連続な単調増加関数であれば,
その逆関数 \(\small x=F^{-1}(y)\) が存在します.
このとき,区間 \(\small [0,1]\) 上の一様分布にしたがう
確率変数を \(\small U\) として
\(\small F^{-1}(U)\) を考えます.
この値が,累積分布関数が \(\small F(x)\)
であるような確率分布にしたがう乱数になります.
なぜならば,
\(\small P(F^{-1}(U)\le x)\) を考えると,
\[\small P(F^{-1}(U)\leq x)=P(U\leq F(x))\] であり,
\(\small U\) が区間 \(\small [0,1]\) 上の一様分布にしたがえば,
その確率密度関数は
\[\small f(u)=\begin{cases} 0 & (1\lt u)\\ 1 & (0\leq u\leq 1)\\ 0 & (u\lt 0)
\end{cases}\]
であるので,その累積分布関数は \(\small 0\leq x\leq 1\) のときは
次のようになります.
\[\small
\int_{-\infty}^{x} f(u) \,du= \int_0^x 1 du=x \]
つまり,\(\small 0\leq x\leq 1\) であれば
\(\small P(U\leq x)=x\) が成り立ちます.
ここで,\(\small 0\leq F(x)\leq 1\) であることに注意すると,
\[\begin{align*}
\small P(F^{-1}(U)\leq x)&\small =P(U\leq F(x))\\
&\small =F(x)\end{align*}\]
となります.これは,\(\small F^{-1}(U)\) は累積分布関数が
\(\small F(x)\) であるような確率分布にしたがうことを示しています.
以上のことを置換積分の計算で確かめるには,下記を参照してください.
|
|
確率密度関数の定番問題として,「次の関数が確率密度関数となるように,
定数の値を定めよ.」という問題があります.
たとえば,次の関数を考えてみましょう.
\[\small f(x)=\begin{cases} 1-ax& (0\leq x\leq 2)\\
\quad 0 & (x\lt 0, 2\lt x)\end{cases}\]
この関数が確率密度関数になるのは,
\[\small \int_0^2(1-ax)\,dx=2-2a=1\]
のときなので \(\small a=\frac12\) のときです.
このとき,累積分布関数 \(\small F(x)\) は,\(\small 0\leq x\leq 1\) のときは
\[\small F(x)=\int_{0}^x\left(1-\frac12t\right)\,dt
=x-\frac14{x^2}\]
となるので,\(\small u=x-\frac14x^2\) の逆関数を求めて,
\(\small x=2-2\sqrt{1-u}\) が得られます.したがって,
累積分布関数の逆関数は,\(\small 0\leq u\leq 1\) のとき,
\[\small F^{-1}(u)=2-2\sqrt{1-u}\]
となります.
下図は,以上のことをMaximaを利用して計算したものです.

(%i3)では,直前で得られた \(\small a\) の値を,
直接 1/2 として入力してもよいのですが,
リスト内の最初の要素(%[1])の右辺(rhs)を取り出することで利用しています.
(%i5)では,直前に得られたリストの第1要素の右辺を Finv(u)
として定義しています.
次に,この Finv(u) に [0,1] 上の一様分布をあてはめると,
確率密度関数が \(\small 1-\frac12x~(0\leq x\leq 1)\) であるような
分布になることを確かめてみましょう.
最初に,記述統計の計算を行うパッケージ「descriptive」を読み込んでおきます.

(%i8)では,Finv(random(1.0)) により,
[0,1] 上の一様乱数の累積分布関数の逆関数 \(\small F^{-1}(u)\) の値を求め,
その値が \(\small n\) 個からなるリストを作成するコマンドを定義しています.
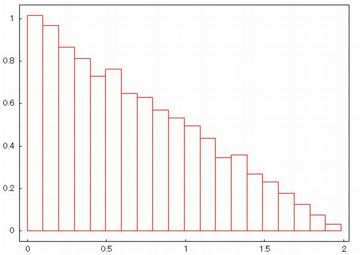
(%i9)では,要素数が10000個の場合のヒストグラムを,
縦軸を確率密度に,柱の本数を20本に指定して描画しています.
下図が描画されます.要素数が少ないと凸凹が生じます.
本数を指定しないと,デフォルトの数である10本で描画されます.
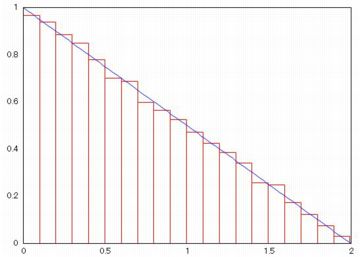
このヒストグラムに確率密度関数のグラフを重ねるには,
「draw2d」を利用します.パッケージ「draw」を読み込むと,
(%i11)により確率密度関数のグラフと重ね描きされます.
その描画コマンドの中でリストを発生させているので,
(%i9)のヒストグラムとは異なります.

|
|
|
■推定・検定
|
|
推定・検定を行うには,それに関する一連の手続きを納めたパッケージ「stats」を
読み込む必要があります.
パッケージ「stats」を読み込むと,統計計算に必要な
記述統計「descriptive」,確率分布「distrib」,そして
結果を表示させる「inference_result」のパッケージも自動的に読み込まれます.
具体的な使用法は,マニュアルの「83. Stats」を参照してください.
簡単な具体例とともに,
各種のコマンドの使用法や出力される結果の見方について解説されています.
ただし,コマンドの使い方が解説されているだけであり,検定の内容が解説されて
いるわけではありません.利用しようとする検定がどのようなものであるかは,
統計の教科書で理解した上で使用する必要があります.
以下に,このパッケージに登録されている主なコマンドを列記します.
- test_mean:平均に関する \(\small t\) 検定
- test_means_difference:平均の差に関する \(\small t\) 検定
- test_variance:分散に関する \(\small \chi^2\) 検定
- test_variance_ratio:分散の比に関する \(\small F\) 検定
- test_proportion:比率の検定
- test_proportions_difference:比率の差の検定
- test_sign:メジアンに関するノンパラメトリック符号検定
- test_sign_rank:メジアンに関するWilcoxonの符号順位検定
- test_rank_sum:メジアンに関するWilcoxon-Mann-Whitney検定
- test_normality:正規性に関するShapiro-Wilk検定
|
|


