
グラフ電卓を活用して数学ロードを駆け抜けよう!
(注) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
■「数学学習」での具体的利用法
[Map]
|
[御案内] このページでは,数ナビ(数式処理電卓)を
数学学習の具体的場面でどのように利用すべきかについて紹介します.
計算結果やグラフの確認のみならず,
計算の途中経過や,自分で抱いた疑問に対しても対応することができ,
数式処理機能を「思考のツール」として活用することできます.
それが,「数学ナビゲーター」と名付けられた所以です.
「数ナビ」を活用して,数学理解をさらに深めていただきたいと思います.
以下では,TI-89titaniumの場合の利用例を示します. | ||
|
| ||
|
[お知らせ] グラフ電卓を所持していないときは, 数式処理ソフトをインストールすると同様のことができます. 多様なOS(Linux, Windows, MacOS, Android)に対応して無料で利用できる 数式処理ソフトとしてMaxima があります.スマホやタブレットにインストールすると, いろいろな式や微積などの計算問題の答えや、 関数のグラフ確認をするとき非常に重宝します。 下記は,Andoroid版の解説本です. コマンドはAndroid版もPC版も同一なので、 iPhone所持の方はPC版のコマンドレファレンスとして利用することができます。 フリーソフトなので,一度試してみてください. いつでも・どこでも・スマホで数学!
|
■方程式 \(\small x^3-3x+2=0 \) を解く
- (1) 方程式 \(\small x^3-3x+2=0\) の解法
-
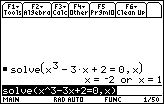
- (2) 式 \(x^3-3x+2\) の因数分解
-
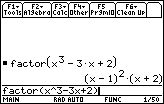
- (3) 式 \(\small x^3-3x+2\) への値の代入
-
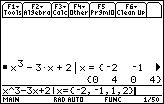
- (4) 除算 \(\small (x^3-3x+2)\div(x+2)\) の計算
-

- (5) 関数 \(\small y=x^3-3x+2\) のグラフ
-
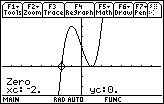
- (6) 関数 \(\small y=x^3-3x+1\) のグラフ
-
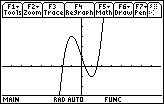
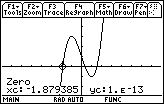
- (7) 関数 \(\small y=x^3-3x+1\) の値の変化
-
解き方が分かっているときは,この機能を利用することで自分の求めた解が 正しいかどうかを確認することができますが, 解き方が分からないときは,どのようにすればよいのでしょうか.
ただし,実際に因数分解するには多項式の除算を行って 商を求める必要があります.多項式の割り算を手計算で行うのは, ちょっと面倒です.
■ 不定積分 \(\small \int\frac{x}{(x+1)(x-2)}\,dx\) を求める
- (1) 不定積分 \(\small \int\frac{x}{(x+1)(x-2)}\,dx\) の計算
- (2) 積分結果の展開
- (3) 微分することによる確認
- (4) 微分の結果を通分することでの確認
- (5) 部分分数分解
- (6) 部分分数分解の計算
- (7) 分母を払う計算
-
- (8) 連立1次方程式を解く
-
有理関数の不定積分の求め方を理解している場合は, 以上のような方法で,表示結果に多少の変形を交えることで 自分の求めた積分結果の確認をすることができます.
では,部分分数への分解の仕方が分からない場合はどのようにすればよいのでしょうか.
\[\begin{align*} \small {\rm solve}&\small (a+b=1~~ {\rm and}\\ &\small -2a+b=0, \left\{a, b\right\})\end{align*}\] TI-Nspireの場合は数式テンプレートを利用します. 結果が \(\small a=\frac13\quad {\rm and}\quad b=\frac23\) として表示されます.
数式処理機能は最終的な結果を表示させるばかりではありません. (5)〜(8)の計算過程も確認できるので,自分の解答が誤っているときは, どの部分の計算を間違えたのかをチェックすることもできます.
■ 微分方程式 \(\small y'+y=e^{-x}\) を解く
- (1) 微分方程式の一般解
- (2) 初期条件を与えた解法
-
- (3) 初期値問題を自分で解く
-
- (4) 勾配場と解曲線
-
一般解から自分で計算して求めるには, 一般解に初期条件を代入して任意定数 @1の値を求めることになります.
数ナビ(数式処理電卓)は, この短い接線を書き込んだ図(勾配場という)を表示することができます. さらに,その図の中で初期値を指定すると,解曲線を描画することができます. 「微分方程式」の大域的な意味を理解させるには、 この図は是非ともみせたいところです。
