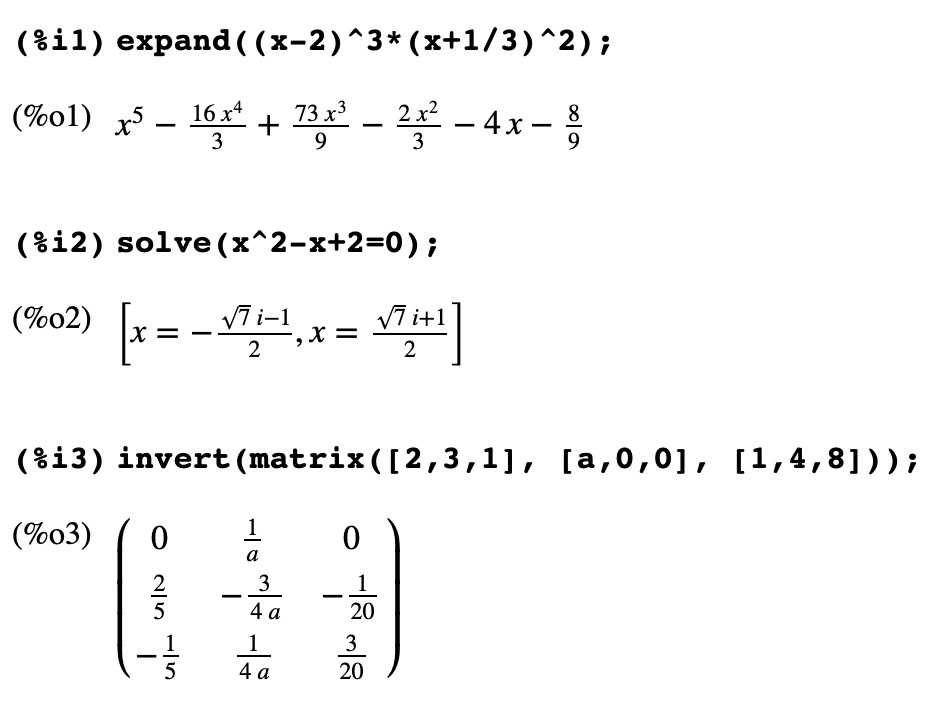�uMaxima�v�����p���Đ��w�̊w�K���[�h���삯�����悤�I
(��) MathJax���g�p���Ă���̂ŁA �X�}�z�ł͕\���Ɏ��Ԃ������邱�Ƃ�����܂��B
���o�C�����p(Android)�ł̃��j���[�I���́A SiteMap�𗘗p���邩�A �u�������v����u�V�����^�u���J���v��I�����Ă��������B
| �� ���������\�t�g�uMaxima�v�����p�������w�w�K �@[Map] |
|
| ||||
|
| ||||
|
[��ē�] �uMaxima�v(�}�L�V�})�́C�t���[�̐��������\�t�g�ł��D
�L���� Mathematica �� Maple �ɗ��Ȃ����x���̐����������\�ł���C
Linux�CWindows�CMacOS�݂̂Ȃ炸�CAndroid�ł�����܂�.
�����ł́C���w�w�K�ł� Maxima �̊��p�@�ɂ��ĉ�����܂��D
�@�Ȃ��C���̒��̑����̂��Ƃ́A �u���K���z�v�ł͂Ȃ��u�x�L���z�v�ɏ]���Ă���悤�ł��B �@�֘A�T�C�g���܂Ƃ߂��u�x�L���z�F�����N�W�v���Q�Ƃ��Ă��������B | ||||
|
[���m�点] �X�}�z(Android)��Maxima�̉���{���o�ł��܂����D �v�Z����O���t�̊m�F������Ƃ��ɔ��ɏd�܂��D �t���[�\�t�g�Ȃ̂ň�x�����Ă݂Ă��������D PC�ł̃R�}���h���t�@�����X�Ƃ��Ă����p�ł��܂��B
| ||||
|
| ||||
| ���uMaxima�v�Ƃ́H |
|
|
|
�@Maxima�̓t���[�̐��������\�t�g�ł��D
���w�ɊS�͂����Ă��C
�u���������v���ǂ̂悤�Ȃ��ƂȂ̂��C���[�W�������Ȃ�����
�����Ǝv���̂ŁC�ŏ��Ɋ���̉�ʂ��Љ�܂��D
�v����ɁC�v�Z���ʂ𐔒l�ŕ\������d��Ƃ͈Ⴂ�C
�u�������̂܂܂̌v�Z���ł���I�v�Ƃ������Ƃł��D
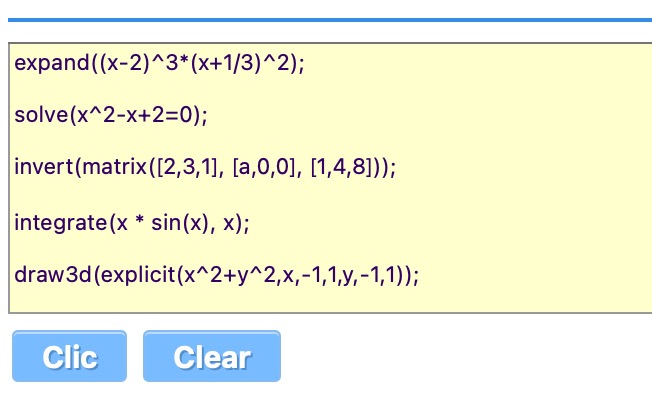
���������Ă���X�}�z��^�u���b�g��Android�̏ꍇ�́C �uMaxima on Android�v�Ƃ����A�v����g�ݍ��߂C PC�݂̂Ȃ炸�X�}�z��^�u���b�g�ł��ȉ��̌v�Z���ł��邱�ƂɂȂ�܂��I �e��̎��̌v�Z�@���}�ł́C���̓W�J(%i1)���������(%i2)�C�������̉�@(%i3)�C �����Ċ��̔����E�ϕ��̌v�Z���s���Ă��܂��D (%i4)�ł� \(\small (\sin x)^2\) �̑�2���������C (%i5)�ł� \(\small e^{-x}\cos{x}\) �� �s��ϕ������߂��Ă��܂��D
���̃O���t �O���t���I���Ď��̃R�}���h��ł����ނɂ́C �O���t��ʂ̉E��́u�~�v�������ăO���t��ʂ����K�v������܂��D �R�}���h�̍Ō���u;�v�ŏI����ƁC �O���t��ʂ����ƃO���t��ʂ������I�ɕۑ������ �ۑ��ꏊ���\������܂��D�u���v(���p)�ŏI����ƁC �O���t���\������邾���ŕۑ��͂���܂���D ���X�ɂ��낢��ȃO���t�������Ƃ��́C �u;�v�ł͂Ȃ��u���v(���p)�ŏI���������悢�ł��D �u;�v�ɂ��Ď����Ă����ƁC ��������ʂ����Ƃ��Ƃ��ۑ�����Ă����̂Œ��ӂ��Ă��������D �@�uplot3d�v�𗘗p����ƋȖʂ�`�����Ƃ��ł��܂��D ���}�́C�u���L�V�J���n�b�g�v�Ƃ��Ă�� \[\small f(x,y)=\frac{\sin\sqrt{x^2+y^2}}{\sqrt{x^2+y^2}}\] �̃O���t�ł��D\(\small f(x,y)\) �����O�ɒ�`���Ă����ƁC ���̃R�}���h�ɂ��`�悳��܂��D �}��ϐ��̃��[�h������C �~�����W�⋅���W�ŕ\���ꂽ�Ȗʂ��`�悷�邱�Ƃ��ł��܂��D ���̃R�}���h��ł����ނɂ́C �O���t��ʂ̉E��́u�~�v�������ăO���t��ʂ���Ă��������D �uplot3d(f(x,y), [x,-10,10], [y,-10,10], [grid,50,50])���v |
|
�����������̉�@
�@(%i11)�ł́C1�K���������� \(\small \frac{dy}{dx}+y=0\) �̈�ʉ������߂Ă��܂��D �u%c�v�͔C�Ӓ萔�ł��D (%i12)�ł́C���O�ɋ��߂���ʉ��̏�������(initial condition) �u\(\small x=0, y=1\)�v �� ����������������߂��Ă��܂��D �u%�v�́C���O�̌���(%o11)�̂��Ƃł��D (%i13)�ł́C2�K���������� \(\small \frac{d^2x}{dt^2}+4x=\cos{t}\) �̈�ʉ������߂Ă��܂��D �u%k1, %k2�v�͔C�Ӓ萔�ł��D (%i14)�ł́C���O�ɋ��߂���ʉ��̏������� �u\(\small t=0, x=0, \frac{dx}{dt}=1\)�v �� ����������������߂��Ă��܂��D
�x�N�g����̕\�� �@����ɂ́C�o�͂��ꂽ������TeX�̏����ɕϊ����邱�Ƃ��ł��܂��D ���Ƃ��C(%o14)�̎���TeX�̏����ɕϊ�����ɂ́C �utex(%);�v�Ƃ��邾���ł��D ����x={{\sin \left(2\*t\right)}\over{2}}-{{\cos \left(2\*t\right) }\over{3}}+{{\cos \left(t\right)}\over{3}}���� (�u���v�͔��p) �@���̏���������I�����ăg�b�v���j���[�́u�ҏW�v���� �u�R�s�[�v���ē\��t���ăR���p�C������C �����Ō��ʂ������������͂��������ƂȂ�(%o14)�̎����\������܂��D (%o15)�ł͉~�}�[�N�u���v���o�b�N�X���b�V���ŕ\������Ă��܂����C �\��t����Ɓu���v�ɂȂ�܂��D �Ȃ��C\(\small \frac{\sin(2t)}{3}\) �͒ʏ�́u\frac{\sin(2t)}{3}�v �ƋL�q����Ǝv���̂ł����C Maxima�ł́u\sin\left(2\*t\right)}\over{2}�v�ƕ\����܂��D ���̂܂܃R�s�[���Ă��C�C�����邱�ƂȂ��R���p�C�����邱�Ƃ��ł��܂��D
Maxima�̗��j �@���̃y�[�W�ł́CMaxima�̃C���X�g�[���̎d���C ��{�I�Ȏg�����C�����Ċw�K��̗��p�@�Ȃǂɂ��ĉ�����܂��D ���w���w�K�����ł́u���������v�̈З͂���������Ă���������K���ł��D Maxima�̍��Z�E��w���N���̃��x���ł̋@�\�́C �`���ŏЉ�����Ђ� �u �����ǂ��v�ɂ���ڎ����Q�Ƃ��Ă��������D ����ɐi��吔�w�ł̋@�\�́C �u �}�j���A���̖ڎ��v���Q�Ƃ��Ă��������D �����_��Q�_�̃p�b�P�[�W�𗘗p���邱�Ƃ��ł��܂��D �@�Ȃ��C���w���w�K���̎҂Ɂu���������v�𗘗p������ƁC �u�v���ێʂ�����āu�w���E���k���l���Ȃ��Ȃ�v�Ƃ������Έӌ��� �q�ׂ�����������܂����C�S���̞X�J�Ǝv���܂��D �l���������Ɋێʂ����Ă���Ƃǂ̂悤�Ȏ������ʂ��҂��Ă��邩�́C �w���E���k���ł��悭��������ł��傤�D �u���w���肽���I�v�ƍł��v���Ă���̂́C �����ł͂Ȃ��w���E���k���g�ł��D �P���ȁu�������킹�v�Ƃ��ė��p���邾���ł��C �傫�ȋ�����ʂ����҂���܂��D����ɐi��ŁC �u�v�l�̃c�[���v�Ƃ��Ďg�p����悤�ɂȂ�C ���w��̎v�l�W�J���傫������������邱�Ƃ����҂���܂��D
Maxima on line
|
|
|
| ���_�E�����[�h�ƃC���X�g�[�� |
|
|
| �_�E�����[�h |
|
�@Maxima�͉��L�̃T�C�g����_�E�����[�h�ł��܂��D
Maxima, a Computer Algebra System �@�u���������v�́C �p���ł́uComputer Algebra System�v�ƌĂ�Ă��܂��D �����āC�P�ɁuCAS�v�ƌĂԂ��Ƃ�����܂��D �_�E�����[�h����ɂ́C�g�b�v�o�[�ɂ��郁�j���[���� �uDownloads�v��I�����܂��D ���}�́C�I����ɕ\��������ʂł��D�@�ȉ��ł́CWindows�ł̏ꍇ�̃_�E�����[�h�̉ߒ��������܂��D
|
|
|
| �C���X�g�[�� |
|
�@�_�E�����[�h����EXE�t�@�C�����͎����𓀃t�@�C���ɂȂ��Ă���̂ŁC
�t�@�C�����N���b�N����Ǝ����I�ɉ𓀂���܂��D
����EXE�t�@�C���́C
�u���E�U�[��[�_�E�����[�h](Ctrl-J)�̉ӏ�����I������Ƃ悢�ł��傤�D
�N���b�N����ƁC������ƊԂ������ĉ𓀍�Ƃ��n�܂�܂��D
�@�𓀂��I���ƃC���X�g�[���[�������オ��܂��D �@�C���X�g�[���̓r���ł́C�ȉ��̎��ɂ��Ċm�F�����߂��܂��D ���ɂ�����肪������C�uOk�v��u���Ɂv�����������Ă���悢�ł��傤�D �@�r���Ŋm�F�����߂����Ȏ����́C���L�̒ʂ�ł��D
�@�ȏ�̎w��ŃC���X�g�[�����J�n����C �I������Ɖ��}���\�������̂Łu�����v���N���b�N���܂��D |
|
|
| �� ���낢��ȁuMaxima�v |
|
|
| wxMaxma |
|
�@�C���X�g�[����ɃX�^�[�g�{�^���������ƁC
�u�ŋߒlj����ꂽ���́v�Ƃ���
�uwxMaxima�v�Ƃ������̂̃A�C�R�����\������܂��D
�@�N���b�N����ƁC���L�̂悤��wxMaxma�̃g�b�v��ʂ�����܂��D ���̉�ʂɃR�}���h����͂��邱�ƂŁC���낢��Ȍv�Z�����邱�Ƃ��ł��܂��D �@�����̏�Ԃł����C����̊p�ŃJ�[�\�����_�ł��Ă��܂��D ���낢��Ȍv�Z��������ɂ́C ���̉ӏ����ŏ��ɗᎦ�����悤�ȃR�}���h�� �ł����݂܂��D ���Ƃ��C�uexpand((x+1)^5)�v�Ɠ��͂��� [shift][Enter] �������ƁC ���͎��̍Ō�Ɂu;�v���t������Č��ʂ��\������܂��D [Enter]�������Ɖ��s����邾���Ȃ̂ŁC ���ʂ�\��������ɂ͕K��[shift][Enter]�������Ă��������D �R�}���h����͒��́C���̍s�̍��[�Ɂu�Ԃ��L���v���\������܂��D Maxima�́C���͂������̋����������߂� ���̍Ō�ɂ́u;�v������ɂȂ��Ă��܂����C wxMaxima�� [shift][Enter]���������Ǝ����͂̏I���Ɣ��f���� �����I�ɒlj����Ă���܂��D �@���}�́C�������̉������߂�R�}���h����͂��Ă���Ƃ���ł��D ���͒��̍s�̍��[�ɂ͐Ԃ��L�����\������Ă��܂��D ���̌��[shift][Enter]�������ƁC ���͂������Ɂu;�v���t������Č��ʂ��\������܂��D N�Ԗڂɓ���(input)�������ɂ�(%iN)�C ���̌��ʂƂ��ďo��(output)����鎮�ɂ�(%oN)�Ƃ����L���������ŕt����܂��D �@�uwxMaxima�v�́CGUI (Graphical User Interface) ������Maxima�𑀍�ł��� �悤�ɂ����\�t�g�E�F�A�ł��DMaxima�̃R�}���h���o���Ă��Ȃ��Ă��C ��ʏ㕔�̃��j���[����ł�Maxima�𑀍삷�邱�Ƃ��ł��܂��D �@���Ƃ��C��ʏ㕔�̃��j���[�Ƀ}�E�X�|�C���^�[�����Ă����ƁC ���}�̂悤�ɓ��{��̃��j���[���\������܂��D���̃��j���[��ʂ��� �R�}���h�����s���邱�Ƃ��ł��܂��D�������C �v�Z���̓��͂����߂���Ƃ��ƁC ���O�̌��ʂɑ��Ă����Ȃ菈�����s����ꍇ�Ƃ����݂��Ă���̂ŁC ���̈Ⴂ�ɂ��Ċ����K�v������܂��D �ʓ|�ł��C�R�}���h����͂�������̕��� �u������Maxima�𑀂��Ă���v���o������̂ł͂Ȃ����Ǝv���܂��D ���}�́C�u������(Q)�v�̃��j���[�ł��D �A����������C�����������̉������߂邱�Ƃ��ł��܂��D
�@Maxia�̊�{�I�Ȏg�����ɂ��ẮC
�u���w�w�K�ł̊��p�v��
�u�����N�W�v���Q�Ƃ��Ă��������D
�����葁���S�̑���c���������ꍇ�́C
�uMaxima��p�������������v
���Q�Ƃ��Ă��������D
|
|
|
| Maxima on Android |
|
�@�uMaxima on Android�v�́C���{�̖{�c�N�W���ɂ�胊���[�X���ꂽ���̂ł��D
���ʂ�TeX�ŏo�͂���܂��D
���̃A�v���́C�uPlay�X�g�A�v����uMaxima on Android�v��
�������邾���ŃC���X�g�[�����邱�Ƃ��ł��܂��D�������C
�X�}�z��^�u���b�g�̓��{����͂̃L�[�{�[�h�Ő�������͂���̂́C
�s�ɂ܂�Ȃ��ł��D
�������͂ɓ�������(�\�t�g�E�F�A)�L�[�{�[�h������̂ŁC
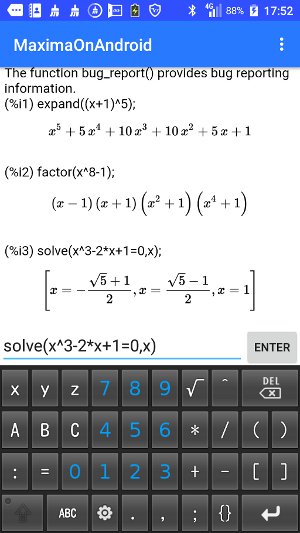
���̂悤�ȃL�[�{�[�h�ɕύX����K�v������܂��D �@���}�́C���̂悤�ȃL�[�{�[�h�ɕύX���Ď��s�������ʂł��D �o�͂���Ă��鎮�́C �ŏ����Ꭶ����Ɠ��l��TeX�ɂ��o�͂���Ă��܂��D 2������3�����̃O���t�`����\�ł���C Maxima(5.41.0)�̂قڑS�@�\���X�}�z��^�u���b�g�ŗ��p���邱�Ƃ��ł��܂��D (2019.03.31����)
�@Maxima on Android�ɂ́CPC�łɂ͂Ȃ�����������܂��D ���Ƃ��C���̂悤�ȋ@�\������܂��D
�@ �J���҂̃T�C�g�ł́C �K���A�Q�C�ȉ~���C�����e�C�g�\�z�C�[�[�^���Ȃǂ� �b�����舵���Ă��܂��D ���̃A�v�����X�}�z��^�u���b�g�ɃC���X�g�[�����Ă����C �v���������Ƃ��C�u���ł��E�ǂ��ł��v�C �ȒP�Ȍv�Z���獂�x�Ȑ��w�I�v�Z�܂ōs�����Ƃ��ł���̂ł��D |
|
|
| TeXmacs |
�@TeXmacs�𗘗p���Ă��C
Maxima�̌v�Z���ʂ�TeX�ɂ��o�͂œ��邱�Ƃ��ł��܂��D
�`���ł��Ꭶ�����TeXmacs�ɂ����̂ł��D
TeXmacs�́C
Wikipedia�ł͎��̂悤�ɉ������Ă��܂��D
�@GNU TeXmacs��GNU�v���W�F�N�g�ŊJ������Ă���Ȋw�Z�p�ɓ����������[�v���܂��͑g�ł̃t���[�\�t�g�E�F�A�ł���DTeXmacs�͂��̋@�\��TeX��GNU Emacs�̒�����������Ă���C�\�[�X�R�[�h�͂ǂ��炩����Ɨ����ď�����Ă��邪�CTeX�̃t�H���g�𗘗p����DTeXmacs��Joris van der Hoeven���J���C�����e�i���X���s���Ă���DTeXmacs���g�����ƂŁCWYSIWYG��GUI�ō\�������ꂽ�������쐬�ł���D�܂������X�^�C����V������`���邱�Ƃ��ł���DTeXmacs�͍��i���ȑg�ŃA���S���Y����TeX�t�H���g�ɂ��C���p�ɑς�����i���̕��������邱�Ƃ��ł���D�@�v����ɁCLaTeX�����������܂܂�(wysiwyg��)�ҏW�ł���C �t���[�̃G�f�B�^�[�ł��D���̊T�v�́C�����I�ł��� GNU TeXmacs (PDF)���Q�Ƃ��Ă��������D �����炭�͉p��_���̍쐬�̂��߂̂��̂ł���C ���{��ł̕����쐬�ɂ͓K���Ȃ��Ǝv���܂��D �g��������{��ʼn�����Ă���T�C�g�́C�������܂���ł����D �@���́CTeXmacs��Maxima�̏o�͎���TeX�d�l�œ����������߂� ���p���Ă���̂ŁCMaxima��g�ݍ��ވȊO��TeXmacs�̎g������ ������܂���D�����ł́CTeXmacs�̃C���X�g�[����Maxima�̑g�ݍ��ݕ��� ���Ă���������܂��D �@TeXmacs��Maxima��g�ݍ��ނɂ́C ���݂̃o�[�W�����ɒ��ӂ��K�v�ł��D �g�ݍ��߂�o�[�W�����ɂ͑���������悤�ł��D ���̏ꍇ�́CTeXmacs�̃o�[�W�����́u1.99.9�v�C Maxima�̃o�[�W�����́u5.38.1�v�Ŏg�p���Ă��܂��D �ȑO�́u5.31.2�v�Ə����Ă��܂������C �ēx�����Ɓu5.38.1�v�ł����v�ł����D Maxima�̃f�t�H���g�ł̃C���X�g�[����́C �Â��o�[�W�����́uC:\Program files (x86)�v�ɂȂ��Ă��܂����C �u5.39.0�v�ȍ~�ł̓��[�g�f�B���N�g��(C:\)�ɂȂ��Ă��܂��D TeXmacs��Maxima�̍ŐV�ł��g�ݍ��߂Ȃ��̂́C ���̃C���X�g�[���悪�قȂ邩��ł͂Ȃ����Ǝv���܂��D �@Maxima�̉ߋ��̃o�[�W������\��������ɂ́C �_�E�����[�h�����1�s�ڂɂ��� �u Files section�v���N���b�N���܂��D ���}�́C�uFiles section�v���N���b�N���ĕ\��������ʂł��D �@�eOS���Ƃ̃t�H���_�[������̂ŁCWindows�ł���uMaxima-Windows�v�� �N���b�N����ƌÂ��o�[�W�����̃��X�g���\������܂��D ���}�́C�uMaxima-Windows�v�̓��e�ł��D �@���̒�����u5.38.1-windows�v(2016-06-12)�̃t�@�C����I������ �_�E�����[�h�ƃC���X�g�[�����s���Ă��������D ������ƌÂ��o�[�W�����ɂȂ�܂����C Maxima���̂�1960�N��ɊJ�����ꂽ���̂Ȃ̂ŁC ���łɏ\���Ȃقǂ̗��j������܂��D�ʏ�g�p�ł́C �����͌Â��Ă����Ɏx��͂Ȃ��Ǝv���܂��D �C���X�g�[���̍ہCwxMaxima�̃V���[�g�J�b�g���쐬���邩�ǂ����� ����܂����C �ŐV�ł�wxMaxima�����łɃC���X�g�[���ς݂̏ꍇ�́C ���̌Â��o�[�W�����̃V���[�g�J�b�g�͍쐬���Ȃ������悢�ł��D �u�쐬(create)�v�Ƀ`�F�b�N�������ƁC�C���X�g�[���ς݂ł��� �ŐV��wxMaxima�̃V���[�g�J�b�g�ɏ㏑������Ă��܂��܂��D �Ԉ���ď㏑�������ꍇ�̓V���[�g�J�b�g���폜���āC �ŐV�ł�wxMaxima�̃V���[�g�J�b�g�� �쐬���Ă��������D |
|
|
|
�@���ɁCTeXmacs���_�E�����[�h���܂��D
���L�̃T�C�g����_�E�����[�h�ł��܂��D
�@���}���g�b�v��ʂł��D
�����ɕ\������Ă���悤�ȕ������쐬�ł���悤�悤�ł��D
�@�uDownload�v���N���b�N����ƁC�_�E�����[�h��ʂɕς��܂��D �@��L�̉�ʂł́C �uTeXmacs-1.99.9-installer.exe�v���_�E�����[�h����悤�ɐݒ肳��Ă��܂��D ���̉ӏ��ɕ\�������t�@�C�����ŐV�łł��D TeXmacs�̌Â��o�[�W�����́C�E�[�ɂ���uanother here�v���N���b�N����� �\������܂��D���}���C�ߋ��̃o�[�W�����̃��X�g�ł��D �t�@�C�����Â����ɕ\�������̂ŁC �㕔�ɕ\�������uLast modified�v���N���b�N���� �ŐV�̂��̂���\�������܂��D �@�Â��o�[�W�������C���X�g�[������Ƃ��́C ���̒�����I�����ăt�@�C����ۑ����܂��D �Ƃ肠�����́C�ŐV�ł��C���X�g�[�����Ă��������D �ۑ����ꂽTeXmacs�̃t�@�C�����_�u���N���b�N����� �C���X�g�[����Ƃ��n�܂�܂��D�ۑ���̃t�H���_�[���� �X�^�[�g�A�b�v�t�H���_�[�ւ̃V���[�g�J�b�g�o�^�Ȃǂ� �m�F�����߂�ꂽ��ɃC���X�g�[�����n�܂�C �I������Ǝ��̉�ʂ��\�������̂ŁC �uFinish�v�������ăZ�b�g�A�b�v�����������܂��D |
|
|
|
�@���ɁCTeXmacs���N�����܂��D�X�^�[�g�{�^����������
�u�ŋߒlj����ꂽ���́v�ɁuTeXmacs�v�̃A�C�R�����\������C
�f�X�N�g�b�v�ɂ������A�C�R�����lj�����Ă��܂��D
���}�́C�ŏ���TeXmacs���N���������Ƃ��̏�����ʂł��D
�N���b�N���ė����オ��܂łɂ́C������Ǝ��Ԃ�������܂��D
�@���̉�ʂ́CTeXmacs���C���X�g�[�����čŏ��ɋN�������Ƃ��̉�ʂł��D ���̉�ʂ́C����������܂��D�I��������ɂ́C �u�t�@�C���v����uTexmacs�����v��I�����邩�C �uctrl-Q�v���������C�܂��͉E�p�́u�~�v���N���b�N���܂��D ������xTeXmacs�𗧂��グ��Ǝ��̂悤�ȉ�ʂɂȂ�܂��D �@���̏�Ԃł́C�܂�Maxima�͎g���܂���D Maxima��g�ݍ��ނɂ́C�g�b�v���j���[�ɂ���u�}���v���N���b�N���āC �\�������T�u���j���[�̍Ō�ɂ���u�Z�b�V�����v���N���b�N���܂��D �}���ł���A�v�������\�������̂ŁC���̒��́uMaxima�v���N���b�N���܂��D TeXmacs��Maxima�̃o�[�W�����ɂ���ẮC ���́u�Z�b�V�����v�̉ӏ��ɁuMaxima�v���\������܂���D �����ł̐����̂悤�ɂ��Ă����܂������Ȃ��Ƃ��́C TeXmacs��Maxima�̃o�[�W����������ɗ��Ƃ��Ď����Ă݂�Ƃ悢�ł��傤�D �@��L�́u�}�����Z�b�V�����v�ŁuMaxima�v���N���b�N����Ɖ��}���\������C ���̉�ʂ�Maxima�𗘗p���邱�Ƃ��ł��܂��D �`�����Ꭶ����́C ���̂悤�ɂ���TeXmacs��Maxima��g�ݍ���Ŏ��s������ʂł��D ������͌��[Enter]�������ƁC ���͎��̍Ō�Ɂu;�v���t������Č��ʂ��\������܂��D [shift][Enter]�Ƃ���Ɖ��s����Ď��s�͂���Ȃ��̂Œ��ӂ��Ă��������D |
|
|
| imaxima |
|
�@Maxima���G�f�B�^�[�̒��ŗ��p���邱�Ƃ��ł��܂��D�uimaxima�v�ł��D
UNIX�̃G�f�B�^�[�Ƃ��Ē�����Emacs��ŗ��p���邱�Ƃ��ł��܂��D
Emacx���imaxima��g�ݍ��݂ƁC�G�f�B�^�[�̒���Maxima�������Ƃ��ł��܂��D
�o�͂�TeX�ɂ��o�͂ɂȂ�܂��D�g�p����Ă���TeX�́uMiKTeX�v�ł��B
�@���ۂɂ�Windows�ł�Emacs�𗘗p���邱�ƂɂȂ�܂����C imaxima��g�ݍ��ނɂ́C �܂�Emacs�Ƃ����G�f�B�^�[�̎g�����ɏK�n���Ă���K�v������܂��D Emacs��Windows�̒ʏ�̃G�f�B�^�[�Ƃ̓L�[�o�C���h���傫���قȂ�̂ŁC ������g�����Ȃ��ɂ͋����u���Ӂv�Ɓu����v���K�v�ł��D �܂��CEmacs���g����悤�ɂ���܂ł̏����i�K�ł́C LISP����̏����I�Ȓm�����K�v�ɂȂ�̂ŁC Windows���[�U�[�ɂƂ��Ă͂��Ȃ�n�[�h����������������܂���D ���Ȃ��Ƃ��C�u������Ǝ����ɂ���Ă݂����v�Ƃ����ӎ����x���ł́C �����Ă݂邱�Ƃ������ł��傤�B �u�g�p���Ă���G�f�B�^�[��Emacs�ɐ�ւ���v�Ƃ��������v�����K�v�ł��D �@���́C�ȑO��Emacs�n�̃G�f�B�^�[�ł��� �uMule�v���g�p���Ă��āC�����ϊ��ɂ� �uSKK�v ���g�p���Ă������Ƃ�����܂��D���̍��ڂ��������߂ɁC �̂��v���o���Ȃ��炿����Ǝ������Ǝv���܂������C ���{����͂��ł���悤�ɂ���Ƃ���ō��܂��Ă��܂��܂����D ���łɁC�g�������̂�Y��Ă��܂��Ă��܂����B imaxima����{��𗘗p�ł���Emacs�͉��L���_�E�����[�h�ł��܂����C ��������ۂɗ��p�\�ȏ�Ԃɂ���ɂ͂��Ȃ�̍�������Ǝv���܂��D �ŏ��̏����t�@�C��(init.el)���ǂ̂悤�ɐݒ肷�邩���|�C���g�ł��D ��imaxima�ł́C���̓��͂Əo�͌��ʂ����̂܂�TeX�̃\�[�X�t�@�C���� �ϊ����邱�Ƃ��ł��āC �ϊ����ꂽ�t�@�C���͂��̂܂܃R���p�C���\�ł���悤�ł��D �S�������ꂽ���͒��킵�Ă݂Ă��������D
|
|
|
| maxima, xmaxima |
|
�@Maxima ���C���X�g�[�����ꂽ�t�H���_�[�̃T�u�t�H���_�[�� [bin]
������C���̒��Ɂumaxima.bat�v������܂��D
���̃o�b�`�t�@�C�����_�u���N���b�N���Ď��s����ƁC
���}�̂悤�� DOS ���[�h�� Maxima �������オ��܂��D
�����ł̓R�}���h����͂��邵���Ȃ����j���[�𗘗p���邱�Ƃ͂ł��܂��C
���̉�ʂł� Maxima �̑S�@�\�𗘗p���邱�Ƃ��ł��܂��D
wxMaxima �ł̓R�}���h���͎��Ɂu;�v���ȗ��ł��܂������C
�����ł́u;�v�������œ��͂���K�v������܂��D
���ʏo�͂́C[shift][Enter] �ł͂Ȃ��C�P�� [Enter] �����ł��܂��܂���D
Maxima ���J�����ꂽ���̓��́E�o�̓X�^�C���́C���̂悤�Ȃ��̂ł����D
�܂�C���ׂĂ��p�����p�L���ŕ\������܂��D �@�Ȃ��CMaxima�ł̓l�C�s�A�����u%e�v�ŕ\���܂��D �I������ɂ� �uquit();�v�Ƃ��邩�C�܂��͉E��́u�~�v���N���b�N���܂��D |
|
|
| iPhone/iPad�̏ꍇ |
Maxima��iOS�ł͒���Ă��܂���D
���������āCiPhone/iPad��Maxima�𗘗p���邱�Ƃ͂ł��܂��C
�����܂������ŗ��p�ł��鐔�������c�[������������̂ŁC
����𗘗p����Ƃ悢�ł��傤�D
�ȉ��ɁC����Љ�܂��D
|
|
|
| �����w�w�K�ł̊��p |
|
|
| ���uMaxima�v�̃����N�W |
�����ł́CMaxima�̗��p�@��������Ă���Web�T�C�g���Љ�܂��D
�R�}���h�̏ڂ����g�����Ȃǂ�m��Ƃ��Q�Ƃ��Ă��������D
|