|
いろいろな関数
|
|
■球面調和関数
掲示板[No.5]で球面調和関数について質問があったので調べてみました.
名前を聞いたことがある程度でしたが,
電子の動きの解析,CGにおけるライティング,
あるいは気象シミュレーションや信号処理などに現れる関数です.
球面上の関数は,この関数を基底としてフーリエ級数のような
級数展開ができるようです.
以下ではシュレディンガー方程式で解説しましたが,
要するに,ラプラシアン \(\small \Delta (\nabla^2)\) を含む方程式
を球座標 \(\small (r, \theta, \phi)\) で考えたときに,
角度成分\(\small (\theta, \phi)\) の満たす関数が球面調和関数です.
この関数は球面上の関数に対して完全正規直交系をなしており,
球面上の任意の関数を球面調和関数を用いて級数展開することができます.
ラプラシアンは物理・工学では頻出するので,
そのことからも球面調和関数の重要性が分かります.
天文学,地球物理学,CGや音響に関わる分野など多くの分野で利用されています.
あらゆる方向からの角度 \(\small (\theta,\phi)\) に関する情報を
球面調和関数を利用して展開することで,
膨大な情報を幾つかの係数値に圧縮できるようです.
その圧縮効果から,物体の形状表現等,
ラプラシアンと関わりのない分野でも利用されています(参照).
球面調和関数の概要について発表したので,参考にしてください.
【注】このページでは,球座標の他に,下記の認識は得ていることが前提となります.
- 演算子 \(\frac{\partial^2}{\partial x^2}
+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\)
をラプラシアンといい,記号 \(\small \Delta, \nabla^2\) などで表す.
シュレディンガー方程式,波動方程式,熱伝導方程式,拡散方程式等,
多くの重要な方程式がラプラシアンを含む形で記述される.
- 積分可能な関数の空間では,積分を用いた内積が定義できる.
- それをもとにすると,関数の大きさ(ノルム)や2つの関数の直交性に関する
議論ができる.
- ベクトル空間では,
任意のベクトルを,基底とするベクトルの線形結合で表すことができる.
同じことを,関数の空間で三角関数を基底として考えたものが
フーリエ級数展開である.
- 関数の空間では,そのような基底として考えることができるのは
直交関数と呼ばれ,三角関数には限らない.
- 上記について未習の場合は,
[6] 直交関数系を参照してください.
|
シュレディンガー方程式
電子が原子核の回りでどのような波を作っているかを考えると,
それはシュレディンガー方程式
\[\small
\begin{align*}
-\frac{\hbar^2}{2m}
\left(\frac{\partial^2}{\partial x^2}\right.
&+\left.\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)
\psi\\
&+V\psi=E\psi
\end{align*}\]
を満たします.
\(\small \hbar\) は換算プランク定数(ディラック定数)です.
この解 \(\small \psi\) は波動関数であり,
\(\small |\psi|^2\)は電子の存在確率を表す確率密度関数であるようです.
方程式の左辺にはラプラシアンが含まれています.この方程式を,
球座標 \(\small (r, \theta, \phi)\) を利用して変形します.
そして,解 \(\small \psi\) を
\[\begin{align*}\small
\psi(r,\theta,\phi)
&\small =R(r)Y(\theta,\phi)\end{align*}\]
と変数分離すると,定数 \(\small \lambda\) に対して,
\(\small R(r)\) は下記の「3.」の方程式を満たします.
それに対して \(\small Y(\theta,\phi)\) は,次のような方程式を満たします.
\begin{align*}
\small \left\{\frac1{\sin\theta}\frac{\partial}{\partial \theta}\right.
&\small \left(\sin\theta\frac{\partial}{\partial \theta}\right)\\
&\small \left.+\frac1{\sin^2\theta}\frac{\partial^2}{\partial \phi^2}\right\}
Y(\theta,\phi)\\
&\small =-\lambda Y(\theta,\phi)
\end{align*}
\(\small V, E\) を含む項は \(\small R(r)\) が満たす方程式に含まれるので,
\(\small Y(\theta,\phi)\) は,
要するにラプラシアンの角度成分に関する固有関数になっています.
この関数 \(\small Y(\theta,\phi)\) が球面調和関数です.
これをさらに
\(\small Y(\theta,\phi)=\Theta(\theta)\Phi(\phi)\)
と変数分離して求めると,
下記の「2, 3」では凄まじいとしか言いようのない計算の結果,
最終的には次のようになるようです(参照1,
参照2,
参照3).
- \(\small \Phi(\phi)\) は,整数 \(\small m\) に対して
\[\small \frac{\partial^2}{\partial \phi^2}\Phi(\phi)=-m^2\Phi(\phi)\]
を満たす.\(\small \phi\) の周期性から
\(\small \Phi(\phi)=\Phi(\phi+2\pi)\) であることと,
\(\small \int_0^{2\pi}|\Phi(\phi)|^2\,d\phi=1\) と規格化することにより,
解を次の式で考えます.
\[\small \Phi_m(\phi)=\frac1{\sqrt{2\pi}}e^{im\phi}~(mは整数)\]
- \(\small \Theta(\theta)\) は,
定数 \(\small \lambda\) が \(\small \lambda=l(l+1)\) の形のときに
解を持ち,整数 \(\small l,~m~(l\ge 0,~|m|\le l)\) に対して
\[
\begin{align*}
\small \left\{\sin\theta\frac{\partial}{\partial \theta}\right.
& \small \left(\sin\theta\frac{\partial}{\partial \theta}\right)\\
&\small +l(l+1)\sin^2\theta\bigg\}\Theta(\theta)\\
&\small =m^2\Theta(\theta)
\end{align*}
\]
を満たします.この解は,
ルジャンドルの培関数 \(\small P_l^m(x)\) を用いて次のように表されます.
\[\small
\begin{align*}
\small \Theta_l^m(\theta)=P_l^m(\cos\theta)
\end{align*}\]
ここで,
ルジャンドルの培関数は,\(\small l\ge 0\) のとき
ルジャンドルの多項式を
\[\small P_l(x)=\frac1{2^ll!}\frac{d^l}{dx^l}(x^2-1)^l\]
とするとき,\(\small m\ge 0\) として次の式で定義される特殊関数です.
\[\small P_l^m(x)=(1-x^2)^{\frac{m}{2}}\frac{d^{m}}{dx^{m}}P_l(x)\]
この関数は,次の性質を満たします.
\[\small P_l^{-m}(x)=(-1)^{m}\dfrac{(l-m)!}{(l+m)!}P_l^{m}(x)\]
\[\begin{align*}
\small \int_{-1}^{1}& \small P^{m}_l(x)P^{m}_{l'}(x)\,dx\\
&\small =
\frac2{2l+1}\frac{(l+m)!}{(l-m)!}\delta_{ll'}
\end{align*}
\]
\(\small \delta_{ll'}\) はクロネッカーのデルタで,
\(\small l=l'\) のときに 1 を,それ以外は 0 の値をとります.
さらに,\(\small P_l^m(x)\) に,
上記の係数の逆数の平方根を掛けた関数を考えると,
その関数は正規直交性をもつことになります.
そこで,
解 \(\small \Theta(\theta)\) としては,
下記の関数を考えることにします.
\[\begin{align*}
\small \Theta_l^m(\theta)=
&\small \sqrt{\dfrac{2l+1}{2} \dfrac{(l-m)!}{(l+m)!}}\\
&\small \times P_l^{m}(\cos\theta)
\end{align*}\]
- \(\small \psi(r,\theta,\phi)=R(r)Y(\theta,\phi)\) と変数分離
したときの \(\small R(r)\) は,整数 \(\small l(l+1)~(l\ge 0)\) に対して
\[
\begin{align*}
\small \left\{\frac{\partial}{\partial r}
\left(r^2\frac{\partial}{\partial r}\right)\right.
&\small \left.+\frac{2mr^2}{\hbar^2}(E-V(r))\right\}\\
&\small \times R(r)=l(l+1) R(r)
\end{align*}
\]
を満たします.この解は,ラゲールの培関数を用いて次の式で表されます.
\[
\begin{align*}
\small R_{nl}(r)&\small =-\left(\frac{2Z}{nr_0}\right)^{\frac32}
\sqrt{\frac{(n-l-1)!}{2n((n+l)!)^3}}\\
&\small \times \exp\left(-\frac{Z}{n} \frac{r}{r_0}\right)
\left(\frac{2Z}{n} \frac{r}{r_0}\right)^l\\
&\small \times L_{n+l}^{2l+1}\left(\frac{2Z}{n} \frac{r}{r_0}\right)
\end{align*}\]
ここで,\(\small Z\) は原子番号,\(\small e\) は電子の電荷,
\(\small r_0=\frac{4\pi\epsilon_0\hbar^2}{me^2}\) であり,
\(\small L_t^s(x)\) はラゲールの培多項式で次の式で定義されます.
\[\small L_t^s(x)=\frac{d^s}{dx^s}\left(e^x\frac{d^t}{dx^t}(x^te^{-x})\right)\]
\(\small n\) は主量子数,\(\small l\) は方位量子数, \(\small m\) は磁気量子数と
呼ばれる整数で,\(\small n\geq l+1\) である必要があります.
以上を元にすると,シュレディンガー方程式の解 \(\small \psi\) は,
1〜3の積として次のように表されます.
\[
\begin{align*}
\small \psi(r,\theta,\phi)
&\small =R_{nl}(r)\cdot \sqrt{\frac{2l+1}{2}\frac{(l-m)!}{(l+m)!}}\\
&\small \times P_l^{m}(\cos\theta)\cdot\frac1{\sqrt{2\pi}}e^{im\phi}
\end{align*}
\]
|
|
球面調和関数
シュレディンガー方程式のようなラプラシアンを含む方程式の解で,
角度依存性に関する \(\small (\theta, \phi)\) の関わる部分,
つまり前述の解で 1, 2 の積で定義される
\(\small Y_l^m(\theta,\phi)=\Theta_l^m(\theta)\Phi_m(\phi)\)
が球面調和関数です.再掲すると,次の式で表されます.
\[
\begin{align*}
\small Y_l^m(\theta,\phi)
=&\small \sqrt{\small \frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}\\
&\small \times P_l^{m}(\cos\theta)e^{im\phi}
\end{align*}
\]
この関数は,前述のルジャンドル培関数の \(\small P_l^{-m}(\theta)\)
に関する性質を利用すると,
\[
\begin{align*}
\small Y_l^{-m}(\theta,\phi)
=(-1)^m&\small \sqrt{\frac{2l+1}{4\pi}\frac{(l-m)!}{(l+m)!}}\\
&\small \times P_l^{m}(\cos\theta)e^{-im\phi}
\end{align*}
\]
となり,符号が微妙に異なります.そこで,
\(\small m\)の符号部分を統一的に表すため,
球面調和関数を次のような式で定義することにします.
\[\begin{align*}
\small Y_l^m(\theta,\phi)
&\small =(-1)^{\frac{m+|m|}{2}}\\
&\small \times \sqrt{\frac{2l+1}{4\pi}\frac{(l-|m|)!}{(l+|m|)!}}\\
&\small \times P_l^{|m|}(\cos\theta)e^{im\phi}
\end{align*}
\]
式の形から,\(\small (-1)^{\frac{m+|m|}{2}}\) は,
\(\small m\le 0\) のときは \(\small 1\),
\(\small m>0\) のときは \(\small (-1)^m\) です.
\(\small e^{im\phi}=\cos\phi+i\sin\phi\) を含むので,これは複素関数です.
ただし,\(\small |m|\leq l\) である必要があります.この関数は,
電子の動きを考える必要のある量子力学・量子化学や電磁気学にとどまらず,
ラプラシアンを含む方程式の解に現れる重要な関数です.
空間におけるいろいろな現象や形状を扱う場合にも必要とされ,
地球物理学,天文学,3次元CAD,3次元CG, 臓器形状、音響等に関する分野でも必須の関数になっているようです[参照].
要するに,経度方向 \(\small \phi\) については通常のフーリエ級数で,
緯度方向 \(\small \theta\) についてはルジャンドル培関数で展開していることに
なります.
この関数について,Maximの機能を利用して考えてみましょう.
\(\small \theta\) は \(\small z\) 軸からの角であり,
\(\small \phi\) は \(\small xy\) 平面における \(\small x\) 軸からの角です
(下図では\(\small \varphi\)).
- 以下では球面調和関数を自前で定義していきますが,
Maximaでは直交多項式のパッケージ「77. orthopoly」
の中で「spherical_harmonic」という関数名で定義されています.
- 球面調和関数は,数式処理のできるグラフ電卓「TI-Nspire CX CAS」で扱うことも可能で,以下に示されるようなグラフを
描画することができます(参照).
- 「TI-89Titanium」や「voyage200」には
曲面の媒介変数モードがないので曲面を描画することはできませんが,
TI-Nspireと同じ定義式で関数を定義して式を表示させることは可能です.
さらに,\(\small \theta, \phi\) のいずれかを固定すれば,
極座標での(平面)グラフを描画することができます.
それは,角を指定して断面図を描くことに相当します.
最初に,上記で定めた関数 \(\small P_l(x), P_l^m(x), \Phi(\phi)\) をもとに,
\(\small Y_l^m(\theta,\phi)\) を定義します.
定義式の中で微分の計算が必要になるので,
下記のように「:=」ではなく「define」を使用します.
「TeXmacs+Maxima」では(%o3)の式が左寄せになりませんでした.
また,スマホでのモバイル表示の関係で(%o2)(%o3)の右側は省いています.
コマンドを改行しながら入力するには,TeXmacs+Maximaでは[shift][enter],
wxMaximaでは[enter]です.

|
|
球面調和関数の絶対値のグラフ
複雑な式で定義される球面調和関数は,
具体的にはどのような式になるのでしょうか.
具体的な \(\small l, m\) に対して式を求めて
グラフを調べてみましょう.
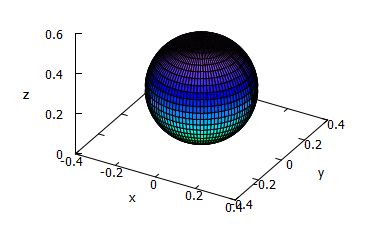
下記は \(\small Y_0^0\) の場合です.
これは,原点からの距離 \(\small r\) が
角 \(\small \theta, \phi\) の値によらず一定ということなので,
原点を中心とする球です(図は略).

\(\small Y_1^0\) の場合は次のようになります.
そのままでは定義式に含まれる微分の計算が行われませんが,
「nouns」をつけることで,計算が実行されます.

次に,この関数のグラフを描画してみましょう.
最初に,計算結果を \(\small f(\theta,\phi)\) として定義して,
その関数の球座標によるグラフを描画させます.
「%」は,直前の式である(%o6)のことです.
Maximaでは,極方程式 \(\small r=f(\theta, \phi)\) のままでグラフ描画が可能です.
オプション変数の「transform_xy」に「spherical_to_xyz」を指定することで,
球座標を直交座標に変換して描画することができます.
「same_xyz」は3つの座標軸の間隔を同じにとり,
「grid」では刻み幅を指定しています.
(%i8)の末尾を「;」にすると,
グラフ画面を閉じたときグラフの情報が保存されます.
単にグラフを確認するだけの場合は「$」として保存されないようにします.

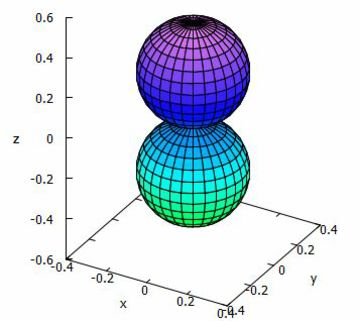
平面の極座標で \(\small r=\cos\theta\) のグラフは,
中心が \(\small (\frac12,0)\) で,原点で \(\small y\) 軸に接する円ですが,
球座標では \(\small \theta \) が \(\small z\) 軸の正の側からの角なので,
任意の \(\small \phi\) で中心が \(\small (0,0,\frac12)\) で原点で
\(\small xy\) 平面に接する円になります.
要するに,その点を中心として \(\small xy\) 平面に接する球です.
しかしながら,「球面調和関数のグラフ」として表示されるグラフは,
\(\small z\leq 0\) の側にも原点で接する球があります.
球面調和関数 \(\small Y_l^m(\theta,\phi)\) は基本的には複素関数なので,
そのままでは3次元グラフとして表示することはできません.上記の2つの場合は
虚部が含まれないので,
そのままの式でもグラフを表示できていますが,
\(\small \frac{\pi}{2}\le \theta\le \pi\) では \(\small \cos\theta\le 0\)
であるので,その部分のグラフは表示されません.
そこで,絶対値を取った関数のグラフを考えます.
絶対値をとった関数を媒介変数表示により
\(\small x=r\sin\theta\cos\phi, y=r\sin\theta\sin\phi, z=r\cos\theta\)
としてグラフ表示すると下図のようになります.ただし,Maximaでは,
空間での媒介変数は \(\small u,v\) を使用する必要があります.
この場合の \(\small r\) は \(\small |f(u,v)|\) になります.
(注1) Maximaでは球座標のグラフを描画できるので,
実際には媒介変数に直す必要はありません(参照).
(注2) 球面調和関数は,グラフ描画ソフト「gnuplot」で扱うことも可能です.
具体的な式を入力すれば描画できるのは当然ですが,
ルジャンドル培関数 \(\small P_l^m(x)\) を用いた式で定義することもできます.
(参照).

|
|
|
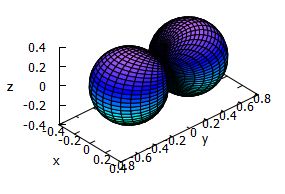
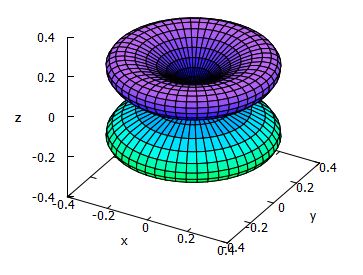
掲示板[No.5]で質問があったのは,
\[\small R_{2,1}(r)\left\{\frac1{\sqrt{2}}\left(Y_1^{1}(\theta,\phi)+
Y_1^{-1}(\theta,\phi)\right)\right\}\]
であるので,括弧内の関数について同様のグラフを考えてみましょう.
下図のように,球が横並びに接するグラフになるようです.

他の場合も同様にして,
球面調和関数の絶対値のグラフを描画することができます.
下図は,球面調和関数のグラフとして例示されることが多い
\(\small Y_2^0(\theta,\phi)\) の絶対値のグラフです.
「%」は直前の結果である(%o17)を表します.

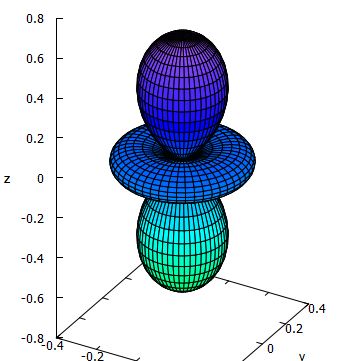
このようにして,球面調和関数の絶対値のグラフを描くことはできますが,
それはラプラシアンを含む方程式の解の角度依存性の部分を取り出して,
その複素関数の絶対値を取って表示しているだけです.
解 \(\small \psi(r,\theta,\phi)\) の意味を正しく把握するには,
その方程式に関する専門知識が必要になります.
|
|
極方程式のグラフ
Maximaでは球座標でのグラフを描画できるので,
何も媒介変数に直す必要はありません(参照).
極方程式のままでグラフを描画できれば,
[eq1,eq2,eq3]への置き換えの手間を省くことができます.
たとえば,\(\small Y_2^0\) の場合は次のようになります.
(%i30)の「trigsimp」は,三角関数を含む式を簡約化するコマンドです.
絶対値を取った関数を \(\small g(\theta,\phi)\) に置きかえていますが,
この置き換えを省略して
plot3dの関数部分を「abs(f(theta,phi))」とすることもできます.
図は前述の画面と同じなので省略します.

グラフが面白いのでいろいろ試してみました.
以下に,グラフだけ紹介します.
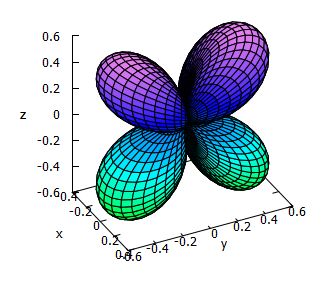
\(\small |Y_2^1+Y_2^{-1}|\)
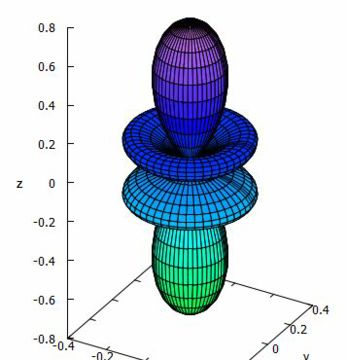
\(\small |Y_3^0|\)
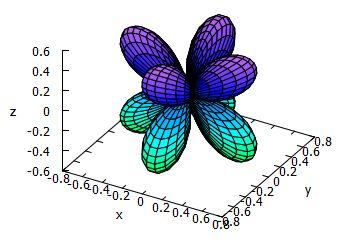
\(\small |Y_3^2+Y_3^{-2}|\)
\(\small |Y_4^0|\)
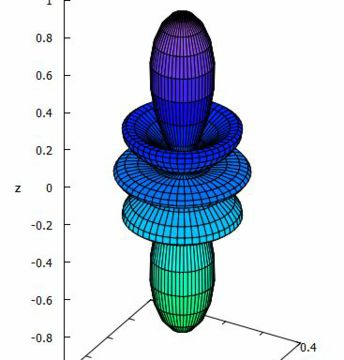
\(\small |Y_5^4|\)

|
|
球面調和関数の実部のグラフ
複素関数である球面調和関数を可視化するとき,
「どの部分を視たいのか」という関心事により,
絶対値ではなく実部(realpart)や虚部(imagpart),
あるいは絶対値の2乗をとる場合もあります
(シュレディンガー方程式の解で \(\small |\psi|^2\) は確率密度関数に
なるようです).
そのため,同じ \(\small Y_l^m\) でもグラフが異なる場合があります.
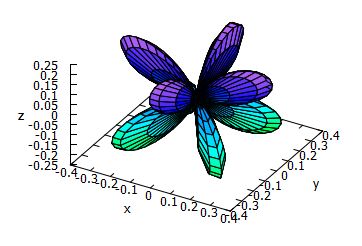
下図は,\(\small Y_5^4\) の実部を取った場合です.
前述の絶対値 \(\small |Y_5^4|\) のグラフとは全く異なります.

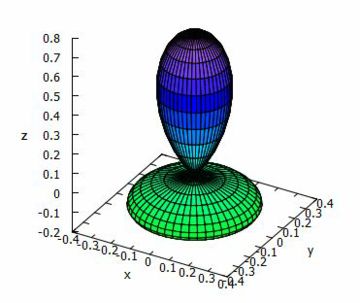
下図は \(\small Y_3^0\) の実部です.
\(\small Y_3^0<0\) の部分は描画されません.

|
|
球面調和関数の性質
球面調和関数は,フーリエ級数の基底としての三角関数と同様の性質を持ち,
球面上の関数に対する完全正規直交性を持っています.
そのため,球面上の関数を球面調和関数を用いて級数展開することができるので,
応用上は極めて重要です.
数学の専門分野のみならず,気象シミュレーション,
CGにおけるライティング(光源からの反射や陰の計算),
あるいは音響の分野など,多数の分野で利用されています
(参照).
以下に主な性質のみを紹介します.
数学的な詳細解説は,
リンク集の関連サイトを参照してください(参照).
ここでは,\(\small Y_l^m\) を \(\small Y_{lm}\) と表すことにします.
- 正規直交性:\(\small Y_{lm}\) は次の性質を満たす.
\[\begin{align*}
&\small \int_0^{2\pi}
\small \int_0^{\pi}Y_{lm}
(\theta,\phi)Y_{l'm'}^{*}(\theta,\phi)\sin\theta\,d\theta d\phi\\
&\small =\delta_{ll'}\delta_{mm'}\\
&\quad (\delta_{pq} はクロネッカーのデルタ)
\end{align*}\]
- 偶奇性:
\[\small Y_{l,-m}(\theta,\phi)=(-1)^mY_{lm}^{*}(\theta,\phi)\]
- 完全性:\(\small f(\theta,\phi)\) を球面上の関数とすると,
次のように展開できる.
\[\small
f(\theta,\phi)=\sum_{l=0}^{\infty}\sum_{m=-l}^{m=l}a_{lm}Y_{lm}(\theta,\phi)\]
ただし,係数は下記の式で定められる.
\(\small Y_{lm}^{*}\) は共役複素数.
\[\small
a_{lm}=\int_0^{2\pi}\int_0^{\pi}f(\theta,\phi)Y_{lm}^{*}(\theta,\phi)
\sin\theta\,d\theta d\phi\]
- ラプラシアンの固有関数:
シュレディンガー方程式の解を
\(\small \psi(r,\theta,\phi)=R(r)Y(\theta,\phi)\) と変数分離すると,
\(\small Y(\theta,\phi)\) は
\[\begin{align*}\small
\left[\dfrac1{\sin\theta}\dfrac{\partial}{\partial \theta}\right.
&\small \left.\left(\sin\theta\dfrac{\partial}{\partial \theta}\right)
+\dfrac1{\sin^2\theta}\dfrac{\partial^2}{\partial \phi^2}\right]
\\
&\small \times Y(\theta,\phi)=-\lambda Y(\theta,\phi)
\end{align*}\]
を満たす.
つまり,ラプラシアンの角度成分に関する演算子の固有関数になっている.
- 加法定理:
2つの単位ベクトル \(\small \mathbf{x_1}, \mathbf{x_2}\)
のなす角を \(\small \theta'\) とし,
\(\small \mathbf{x_1}, \mathbf{x_2}\) の単位球面上の座標をそれぞれ
\(\small (\theta_1,\phi_1), (\theta_2,\phi_2)\) とすると,
次の式が成り立つ.
\[
\begin{align*}
\small P_l&\small (\mathbf{x_1}\cdot\mathbf{x_2})
=P_l(\cos\theta')\\
&\small =\dfrac{4\pi}{2l+1}
\sum_{m=-l}^{l}Y_{lm}(\theta_1,\phi_1)Y_{lm}^{*}(\theta_2,\phi_2)
\end{align*}\]
- ウンゼルトの定理:
\(\small m\) に関する和に関して次の式が成り立つ.
\[\small \sum_{m=-l}^{l}|Y_l^m(\theta,\phi)|^2=\dfrac{2l+1}{4\pi}\]
|
実球面調和関数
球面調和関数は \(\small e^{im\phi}\) を含むので,
\(\small e^{-im\phi}\) と組み合わせると虚数単位を含まない形で
表すことができます.
それは,要するに \(\small Y_l^m(\theta,\phi)\) の実部と虚部を
取ったものです.以下では,\(\small m>0 \) とし,
\(\small y_l^0=Y_l^0\) とします.
\[\begin{align*}
\small y_l^m
&\small =\dfrac{(-1)^mY_l^m+Y_l^{-m}}{\sqrt{2}}\\
&\small =\sqrt{2}{\rm Re}\,((-1)^mY_l^m)\\
&\small =\sqrt{2}K_l^mP_l^m(\cos\theta)\cos{m\phi}\\
\small y_l^{-m}
&\small =\dfrac{(-1)^{m}Y_l^{m}-Y_l^{-m}}{\sqrt{2}i}\\
&\small =\sqrt{2}{\rm Im}\,((-1)^{m}Y_l^{m})\\
&\small =\sqrt{2}K_l^{m}P_l^{m}(\cos\theta)\sin(m\phi)
\end{align*}\]
ここで,\(\small P_l^0(\cos\theta)\), \(\small P_l^m(\cos\theta)\cos{m\phi}\),
\(\small P_l^m(\cos\theta)\sin{m\phi}\) の直交性から,
球面上の関数 \(\small f(\theta,\phi)\) は次のような形に展開することもできます.
展開の形はそれぞれの専門分野で異なり,
物理・工学系は \(\small e^{im\phi}\) を含む形で,
地球物理学などでは下記の形で考える場合が多いようです.
\[\begin{align*}
\small f(\theta,\phi)=\sum_{l=0}^{\infty}\sum_{m=0}^{l}
&\small (a_{lm}\cos{m\phi}\\
&\small +b_{lm}\sin{m\phi})P_l^m(\cos\theta)
\end{align*}\]
ここで,係数 \(\small a_{lm}, b_{lm}\) は次の式で表されます.
ただし,\(\small a_{l0}\) の分母は \(\small 2\pi\) を
\(\small 4\pi\) で置き換えるものとします.
\[\begin{align*}
\small a_{lm}=\dfrac{2l+1}{2\pi}
&\small \dfrac{(l-m)!}{(l+m)!}\int_{0}^{2\pi}\!\int_{0}^{\pi}
f(\theta,\phi)\\
&\small \times P_l^m(\cos\theta)\cos{m\phi}\sin\theta\,d\theta\,d\phi\\
\small b_{lm}=\dfrac{2l+1}{2\pi}
&\small \dfrac{(l-m)!}{(l+m)!}\int_{0}^{2\pi}\!\int_{0}^{\pi}
f(\theta,\phi)\\
&\small \times P_l^m(\cos\theta)\sin{m\phi}\sin\theta\,d\theta\,d\phi
\end{align*}\]
下図は,実球面調和関数の絶対値 \(\small |y_l^m|\) のグラフです.
\(\small l\) が増えるごとに突起の数が増えていき,
\(\small m\) の値が異なるごとに突起の方向が変わっていきます.
右上の小さい球は,球面上の濃淡で表した場合です.
複雑な物体やいろいろな方向からくる情報は,
それを球面調和関数で展開することで,
いろいろな方向の突起を足し合わせることで
表現することができるようです.
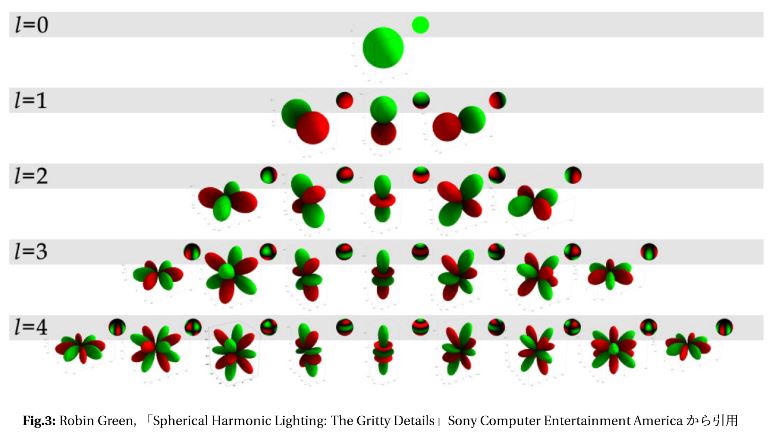
|
|
下図は,Maximaによる実球面調和関数 \(\small |y_5^m|~(m\ge 0)\) のグラフです.
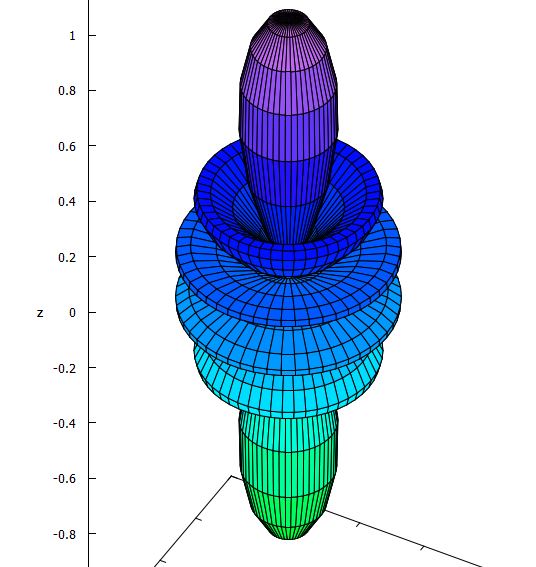
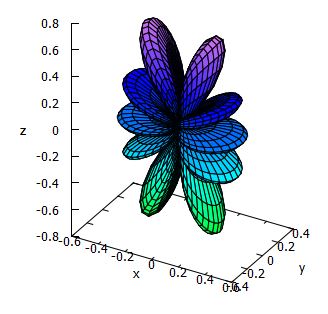
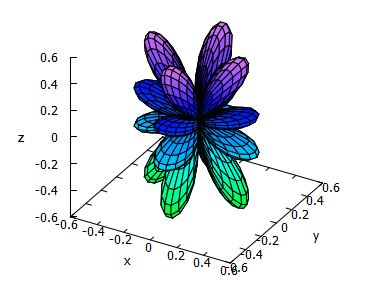
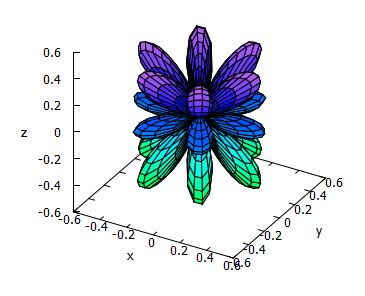
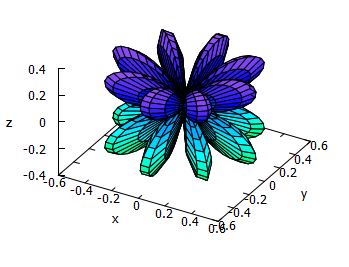
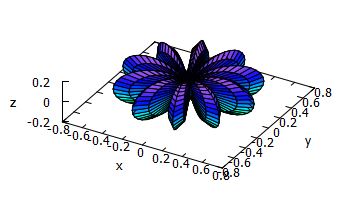
この実球面調和関数のグラフを描画するアプリ
(exeファイル)があります.このアプリを利用すると,たとえば \(\small |y_8^4|\)
のグラフは次のように表示されます.

|
|
Maximaのパッケージ
この球面調和関数に関する解説の大部分を書き終えてから,
Maximaにはこの関数が定義されているパッケージがあることを
下記のサイトで気づきました.
球面調和関数は,直交多項式のパッケージ「77. orthopoly」に含まれています.
さらに,そのパッケージを新たに読み込まなくても,
関数名のコマンドである「spherical_harmonic」が入力されると,
そのパッケージが自動的に読み込まれるようです.
前項で述べたように,
球面調和関数は直交関数と呼ばれる関数群に属します.
パッケージ「orthpoly」には,そのような関数が多数登録されており,
ラゲール多項式,ルジャンドル多項式,ハーミット多項式なども含まれています.
上記サイトでは極座標から直交座標への変換例も紹介されているので,
このサイトにしたがい実際にやってみましょう.

ここまで定義してきた \(\small Y_3^3\) では,
(%o1)で表示される式に「\(\small -\)」が付いています.
他のサイトで示されている式も「\(\small -\)」が付いているので,
おそらくMaximaで定義されている関数は,
\(\small Y_l^m\) の定義式の符号部分 \(\small (-1)^{\frac{m+|m|}{2}}\)
が省略されているのではないかと思われます.
(%i2)で実部を取り出し,(%i3)では \(\small \sin^3\theta\) を
3倍角の公式を利用して展開しています.

(%i4)のコマンド「ratsubst(A,B,C)」は,
「Cの式でBの部分をAで置きかえる」というコマンドです.
球座標と直交座標の間では \(\small z=r\cos\theta\) であるので,
\(\small \theta={\rm acos}\,(z)(=\cos^{-1}(z))\) と置き替えたことは,
\(\small r=1\) が仮定されていると思われます.
なお,(%o4)の右側を省略しています.
(%i5)にある「atan2(y,x)」は逆正接関数です.
\(\small \tan\phi=\frac{y}{x}\) であるので,「ratsubst」により
\(\small \phi\) を \(\small \tan^{-1}(y/x)\) で置きかえようとする
ものです.ただし,
「atan(y/x)」は \(\small -\frac{\pi}{2}\sim\frac{\pi}{2}\)
の範囲での値を求めるので,
\(\small x\lt 0\) の場合はうまくいきません.
そのような場合にも対応できるように,
「atan2(y,x)」は \(\small -\pi\sim\pi\) までの間で
\(\small \tan^{-1}(y/x)\) の値を求めるコマンドです.
(%i6)では,\(\small x^2+y^2\) を \(\small 1-z^2\) で置きかえているので,
\(\small x^2+y^2+z^2=1\) という条件の下で考えていると思われます.
単なる置き換えではなく,式の簡約化も同時に行われます.
★ \(\small r=1\) で考えると,球面調和関数は
\(\small x,y,z\) の多項式で書き表すことができるようです.
直交座標でラプラスの方程式 \(\small \Delta \psi=0\) を満たす
多項式で,\(\small \psi(kx,ky,kz)=k^n\psi(x,y,z)\) を満たすような
関数が球面調和関数であるようです.
(参照).
|
|
リンク集:球面調和関数
この項目を記述するにあたっては,下記のサイトを参照させていただきました.
[1] 球面調和関数の可視化
-
球面調和関数のシミュレーション
\(\small l=0,1,2,3\) の場合の実部のグラフが紹介されています.
-
水素原子の軌道のイメージ
\(\small \phi=0\) の場合について,\(\small \theta=0,30,60,\ldots\)
の場合の値を求めて得られる曲線を \(\small z\) 軸のまわりに回転させる
ことでグラフが描かれています.
-
位相で見る波動関数
球面調和関数を,振幅を明るさ,位相を色と対応させた
カラフルな図が紹介されています.
-
Spherical Harmonic
球面調和関数について,いろいろな側面から可視化されています.
-
3D Spherical Plotting of Sphecical Harmonics: Desmos
Web上のグラフ描画ツールである「Desmos」により,
\(\small Y_l^m\) のグラフをインターラクティブに確認することができます.
絶対値ではなく実部を描いているようです.
操作方法の解説はありませんが,おそらく \(\small n_0\) は分割数と思います.
デフォルトの画面では \(\small l_f=8, m_f=3\) ですが,
確認の意味で \(\small l_f=2, m_f=0\) として確認するとよいでしょう.
左側メニューの下の方にある \(\small a,b,c\) で視点を,
\(\small a_l\) では座標軸の長さを調整することができます.
-
球面調和関数.exeとは何か
実球面調和関数のグラフを
表示するアプリケーションをダウンロードすることができます.
以前に、「数理科学美術館」に登録されていたファイルです.
書籍化にともないサイトは閉鎖されましたが,
アプリだけはVector経由で利用できます.
[2] 球面調和関数の解説
□要点解説
-
球面調和関数[PDF]
球面調和関数のいろいろな性質について簡潔にまとめられています.
-
Wikipedia:球面調和関数表
球面調和関数 \(\small Y_l^m\) について,
\(\small 0\leq l\leq 10\) の場合の式が具体的にまとめられています.
-
球面調和函数
球面調和関数について,数学的な側面についてまとめられています.
□詳細解説
-
量子力学の基本と球面調和関数の可視化
球面調和関数と、その可視化について解説されています.
-
量子力学I/球面調和関数
球面調和関数の定義関数である \(\small \Theta_l^m(\theta)\) や
\(\small \Phi_m(\phi)\) が正規直交完全な固有関数系になっていることや,
球面調和関数の特徴・形状,実関数表示などについてまとめられています.
-
テイラー,フーリエ,球面調和関数
球面調和関数が,フーリエ級数における三角関数ような
正規直交系をなすことについて解説されています.応用としては,
光源が動くときの静的オブジェクトのライティングを考えるとき,
球面調和関数を利用した級数展開が行われているようです.
-
物理地学の基礎:地磁気ポテンシャル
地磁気ポテンシャルを考える中でラプラスの方程式が得られ、
それを解いて球面調和関数が導出されるまでの計算過程が解説されています。
-
球面調和関数を用いた3次元波動方程式の解
音響理論の立場から,球面調和関数を導出するまでの過程が解説されています。
-
物理数学:球面調和関数[PDF]
ラプラスの方程式について級数を利用した解法が示されており、
そこから球面調和関数が構成されるまでが解説されています。
-
CGのための球面調和関数[PDF]
球面調和関数の詳細と、CGでの利用のされ方について解説されています。
-
地球物理学のための球面調和関数ノート[PDF]
全球面上の任意の分布を持つ量は、球面調和関数の重ね合わせにより
表現できることが解説されています。
-
回転群と球面調和関数
回転群、四元数、球面調和関数について解説されています.
-
球面調和関数
球面調和関数に関して、いろいろなな観点からの解説が登録されています.
-
超球面調和関数
球面調和関数は3次元のラプラス方程式の解の角度成分に関する関数ですが,
この関数は4次元以上の高次空間でも定義できるようです.
ただし,4次元以上では一意的な極座標変換は不可能であることから,
幾つかの変換方法があるようです.
-
球面調和函数の性質
球面調和関数の性質について,YouTube動画で解説されています.
□多項式表現での解説
-
球面調和関数の多項式表現
球面調和関数を実数のみで扱う場合や,直交座標での記述等について
述べられています.\(\small r=1\) の単位球上で考えれば,
球面調和関数は \(\small x, y, z\) の多項式で表すことができるようです.
-
体球調和関数と球面調和関数
球面調和関数は,ラプラスの方程式を満たす \(\small n\) 次の同次多項式
\(\small f(x,y,z)\) を,球面上に制限した関数であることが解説されています.
-
Maximaで球面調和関数展開
球面調和関数はMaximaのパッケージで定義済みです.
その関数を利用して直交座標での多項式に変換する過程が示されています.
|
|
[3] シュレディンガー方程式の解法
[4] プログラム
-
水素原子の波動関数ビューア
HTML5の「WebGL+Javascript」を利用した物理シミュレーションとして,
水素原子の電子状態を表す波動関数を可視化することができ,
プログラムソースが公開されています.
-
球面調和関数とその可視化
球面調和関数の概要と可視化について,pythonのスクリプトが紹介されています.
-
水素原子の原子軌道の可視化
水素原子の原子軌道の可視化について、EGWSとAVSを組み合わせた手法について
解説されています。.
-
球面調和関数を視覚化してみまして
球面調和関数はコンピュータ・グラフィックスの世界で利用されていて,
いろいろな方向からの光を球面調和関数で展開して光の情報を展開係数に
圧縮しようとするようです.
processingを用いたコードを入手することができます.
-
球面調和関数の回転
球面調和関数のグラフを回転するとき,
回転後の係数の計算式が例示されており,
pythonでの作成例が提示されています.
-
Math World:Spherical Harmonic
Mathmatica の販売元 Wolfram の英文サイトで
球面調和関数についての解説されています.
\(\small x, y, z\) に変換した式も紹介されています.
-
SHTOOLS
球面調和関数の各種利用に関する、
Pythonのソフトウェアが登録されています(英文).
|
|
[5] 球面調和関数の応用例
□CGでの利用
□他の分野での利用
[6] 直交関数系と直交多項式
□直交関数系
□直交多項式
|
|


