gnuplotを利用してグラフの作成ロードを駆け抜けよう！
(注) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
| ■ 「gnuplot」によるグラフの作成 [Map] |
|
| ||
|
| ||
|
[御案内] TeXを利用した数学プリントの作成では，
関数のグラフをどのように作成するかは大きな問題です．
ここでは，フリーのグラフ描画ソフト「gnuplot」を用いた
グラフの描画方法とTeXへの取り入れ方について解説します．gnuplotは，
数式処理ソフトMaximaにも組み込まれているソフトです．
離散的な実験データのグラフ化や2変数関数のグラフも描画することができ，
理工系の研究論文の図の作成にも利用されています．
Ｃ言語で作成された関数ライブラリーを利用することもできます．
なお，関数のグラフ描画ソフトとしては，gnuplotの他に下記のようなソフトもあります． WinTpic， Ngraph， GRAPES， FunctionView， GeoGebra， Cinderella ★gnuplotを利用しなくても、TeXの中でMetaPostを利用して 立体図形や曲面描画を可能にする「MePoTeX」というマクロパッケージがあります。 その解説ページを作成したので参照してください。 たとえば、 下記のような図をTeXのソースコードの中に簡単に記述でき、 パラパラ漫画まで作成することができます[概要]。最後のグラフは、球面調和関数のグラフです [概要]。
★このページには数学絡みで訪れる方が多いと思われますが、
| ||
|
[お知らせ] 下記を出版しました。 PCやスマホで使える数式処理ソフト Maximaの解説書です。 計算問題やグラフ問題の解答を作るときに非常に重宝します。 フリーソフトなので一度試してみてください。 なお、Maximaでのグラフ描画ではgnuplotが利用されています。 PC版Maximaでグラフを描いてeps保存すれば、 数学のプリント作成の際にも利用することができます。
| ||
|
|
| ■3次元グラフの描画 |
|
|
| 2変数関数のグラフ |
2変数関数 \(\small z=f(x,y)\) のグラフを描画するコマンドは「splot」です．
一様双曲面 \(\small z=x^2-y^2\) は次のように表示されます．
目盛りの間隔は自動で設定されています．
このグラフに対して，2次元グラフの場合と同様に様々な設定をすることができます．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
範囲の設定は，次のようにグラフ描画の「splot」と一緒に行うこともできます．
以下を試してみるときは，「unset」を用いて，
「set」による指定を初期化してから実行してください．
メッシュの間隔は「set isosample」により調整することができます．
「set iso」でもかまいません．
デフォルトでは「set isosample 10,10」で設定されており，
\(\small x\) 軸と \(\small y\) 軸がそれぞれ10本の格子線で区切られています．
同じ本数でよいときは「set isosample 10」とすることもできます．
下図は \(\small x\) 軸を50本，\(\small y\) 軸を30本として，本数を変えた場合です．
この色づけを底面にだけ行うには，
「set pm3d at b」とします．
底面の色づけ部分だけを取り出すには，
「set pm3d map」とします．
色づけの調整は，ある程度上級レベルである必要があります．
詳細は下記を参照してください．
当然ながら \(\small f(x,y)=x^2+y^2\) のグラフと同一ですが，
凡例には「u, v, f(u,v)」と書かれていて媒介変数のモードで
描画されていることを示しています．
|
この円柱に，同じ半径を持ち中心軸が \(\small y\)軸の円柱を交差させて
みましょう．
グラフ画面では縦方向に収縮して表示されるので，
縦方向にちょっと伸ばしてみます．
この2つの円柱の共通部分の体積を求める問題は，
重積分の応用の定番問題です．
内部の共通部分については
|
\(\small z\) 軸方向がつぶれて表示されるので，
下記ではグラフ画面の縦方向を伸ばしています．
このトーラスを縦にするには \(\small y, z\) を交換します．
さらに，\(\small x\) 軸方向に平行移動すると
次の図が得られます．
有名なメビウスの帯を描くこともできます．
クラインの壺も試してみるとよいでしょう．
方程式はWeb検索してください．
同様にすると，同じ半径の円柱面が直角に交差したときの共通部分も
描画できます．下記は，$\small x^2+y^2=4, x^2+z^2=4$の共通部分です．
| 空間曲線と断面曲線 |
|
|
|
これを，幾つかの断面曲線を描画することで，
それなりに曲面をイメージできるようにすることもできます．
全部同一色で指定しました．
繰返しの「
| 陰関数で表された関数のグラフ |
|
gnuplot には，
\(\small f(x,y)=0,~f(x,y,z)=0\) のような陰関数で表された関数のグラフを
描画する機能はありません．ただし，
2次元グラフ \(\small f(x,y)=0\) は
曲面 \(\small z=f(x,y)\) と \(\small xy\) 平面との交線として描くことができ，
それは等高線を描画することで実現できます．
たとえば，「8の字」曲線(レムニスケート)は， 極座標では \(\small r^2=2\cos{2\theta}\) と表されます． この曲線は極座標モード(set polar)にするか， または媒介変数(set parametric)を 利用すると描くことができますが， ここでは曲面の等高線として描画してみましょう． この方程式は \(\small r^4=2r^2(\cos^2\theta-\sin^2\theta)\) であることから， 直交座標では \(\small (x^2+y^2)^2=2(x^2-y^2)\) と表されます． そこで，2変数関数 \(\small f(x,y)=(x^2+y^2)^2-2(x^2-y^2)\) を考えて， そのグラフと \(\small xy\) 平面との交線を考えることにします． 最初に，画面設定を次のようにしておきます． 「reset」して入力し直すか， または基礎設定を保存しておいてロードするとよいでしょう． 保存・ロードのやり方は次の項目を参照してください．
次に，等高線が表示されるようにして，
本数を1本だけにして描画します．
底面に曲線が表示されます．\(\small xy\) 平面上の曲線としてみるには，
「unset surface」として等高線だけが表示されるようにして，
さらに「set view 0,0」により視点を真上に設定します．
凡例や \(\small z\) 軸のラベルが気になるときは，
それら消去します(参照：凡例)．
下図は，座標軸やグリッドを書き入れ，
範囲を狭めて縦横の目盛りの間隔が揃うようにしたものです．
3次元グラフ \(\small f(x,y,z)=0\)を描画する機能は
gnuplotにはありません．
ただし，関数のグラフ描画にgnuplotが使用されている
「Maxima」を利用すると，
\(\small f(x,y,z)=0\) で表された曲面を描画する機能(draw3d)があります．
下図は，Maximaによる \(\small x^2+y^2-z^2=1\) と
\(\small x^2+y^2+z^3=1\) のグラフです．
|
| ■履歴とグラフのファイル保存 |
|
|
| 履歴ファイルの保存と読み込み |
|
gnuplotでいろいろ試しても，
終了すると履歴は全て消えてしまいます．また，
gnuplotを起動するごとに，
座標軸の表示や軸の範囲を設定するのは面倒です．
そのようなときは，設定が共通と想定される状況を書き込んでおいて，
その状況を保存しておきます．
そして，gnuplotを起動するごとに保存した設定を読み込むようにするとよいでしょう．
ここで，共通設定を指定するために，いったんgnuplotを終了します． 「quit」か「exit」を入力するか，または画面の右上の「×」をクリックします． その上で，改めてgnuplotを起動して， たとえば下記を入力します．
ここでは，座標軸を表示し， 縦軸と横軸の目盛りの間隔が同じように見えるように 縦軸の長さを横軸の長さの70％にしています． 関数を具体的に定義した後は， そのグラフを見ながら範囲を適当に調整するとよいでしょう． この履歴を保存するには，
とします．「filename」の箇所は適当に決めてよいですが， 後で思い出せるような名前にしておいた方がよいでしょう． ファイル名は「'」か「"」で囲います． 単なるテキストファイルとして保存されます． 拡張子は「.plt」とする場合が多いようです． ファイルはMy Documentsに保存されます． 単なるテキストファイルとして保存されますが， 自分で入力した内容ばかりではなく， 起動してからユーザーが利用可能になるまでにgnuplotが内部で行っている， 細々とした諸設定も一緒に書き込まれます． その内容を理解しようとする必要はありませんが， プログラムに堪能な方は， 細々部分でgnuplotがどのようなことを行っているのかを知るために 眺めておくとよいでしょう． 「save」を実行したらgnuplotをいったん終了して， 改めて立ち上げます．そして，保存したファイルを読み込むために 下記を実行します．
|
|
|
| グラフ画面の保存 (PDF) |
|
描画されたグラフ画面をファイルに保存するには，
どのファイル形式で保存するかを意識する必要があります．
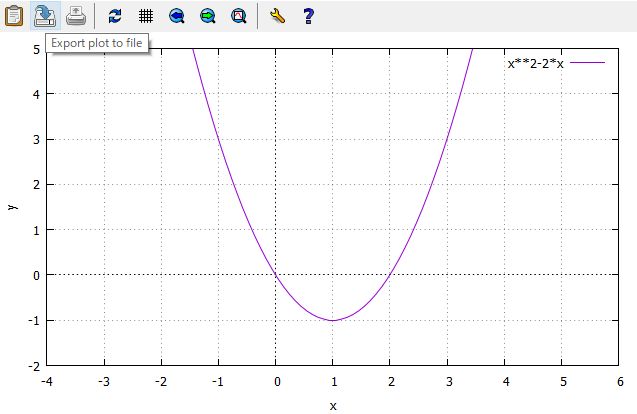
png, pdf, svg, emfのいずれかで保存するには，
グラフ画面の上部で左から2番目のアイコン「Export plot to file」
をクリックします．
保存先のフォルダー，ファイル名，そしてファイル形式を選択すれば
グラフ画面が保存されます．
下記は，ファイル名を「sample」とし，
ファイル形式は「pdf」を指定して保存しています．
「pdf」保存するには、「印刷」画面から 「Adobe PDF」か「Microsoft Print to PDF」を選択して保存することもできます。 ただし、そのファイルには、画像の下に余分な空白が含まれています。 それを削除するには「こちら」を参照して下さい。 削除後のファイルは、\includegraphics を利用すると TeX のファイルで利用することができます。 ただし，gnuplotのバージョンによっては， グラフ画面の上段の表示が若干異なります． ver5.5では，FDマークの保存画面から emf 形式での保存ができ， 「option」の箇所から emf, png, bmp, JPEG, GIF, TIFF のタイプの保存ができます．
出力されたファイルは， 「sample.pdf」というファイル名で「My Documents」に保存されます． この保存場所は， gnuplotの「ファイル(F)」のメニューで表示される 「ディレクトリーの移動」箇所を利用すると変更することができます(下図)． 作成したファイルを事後に利用するのであれば， 扱いやすいフォルダーに変更しておいた方がよいでしょう．
上記のメニューからフォルダーを指定して「Ok」を押すと， gnuplotの画面には，
|
|
|
| グラフ画面の保存 (EPS) |
|
gnuplotは，描画されたグラフ画像を上記以外のファイル形式でも
保存することができます．その保存のためには，
グラフを描画する出力先を変更する必要があります．
デフォルトでのグラフの出力先は「wxt」になっています．
どのような出力先があるかは，「set terminal」を実行すると表示されます．
下記は，表示されたファイル形式の最初の部分を示したものです．
非常に多数のファイル形式に対応していることが分かります．
gnuplotの画像を「eps」形式のファイルで保存するには， グラフを表示した後に出力先を「postscript」に指定して次のように入力します． 同様に，「gif」で保存するには「set terminal gif」， 「jpeg」で保存するには「set terminal jpeg」とします．
最後に「set terminal wxt」を実行しないと， 次にグラフを描画したときにグラフが画面に表示されないので注意してください． または，次のようにしてもかまいません．
ただし，座標軸やタイトルなどに日本語を使用してeps保存すると， 日本語部分が文字化けします． フォントを指定する必要があるようなのですが， いろいろ試してもうまく表示させることができませんでした． 下記を参照して試してみてください． どうしても日本語を使用したい場合は， 出力したファイルを修正して対応することもできます． 「epslatexによる出力」を参照してください．
|
|
|
| グラフ画面の保存 (その他) |
グラフ画面をgnuplotの機能を利用して保存する方法について説明してきましたが，
画面保存をするには他にもいろいろな方法があります．
いずれも，png, jpeg, bmp, gif, tifなどのファイル形式で保存することができます．
|
| ■TeXへの取り込み |
|
|
| \includegraphicsの利用 |
保存したepsファイルは，「graphics」パッケージを利用すると
TeXに組み入れることができます．
基本的には，
「\includegraphics{sample.eps}」とするだけです．
下記では，
画像部分がはっきり分かるよう\fboxにより外枠をつけています．
また，上記のファイル指定は， EPSファイルがTeXのソースファイルと同じフォルダーにある場合です． たとえば，ソースファイルが置かれているフォルダーの サブフォルダー「sub」に置かれているときは \includegraphics{./sub/sample.eps}とします． 下図は，表示されたDVIから画像部分を切り取ったものです．
ここでは「eps」ファイルでの利用を想定して解説していますが、 近年は「eps」ではなく「pdf」ファイルにして取り込む流れになっているようです。 その場合は、前述したように「pdf」で保存して、 拡張子が「pdf」のまま \includegraphics を利用します。 ただし、画像の下に余分な空白が含まれてしまうので、 それを削除する必要があります。 TeXの「bin」フォルダーにある「pdfcrop.exe」を利用すると、 余分な空白が削除されます(参照)。 |
|
|
| \includegraphicsのオプション |
\includegraphicsには，
いろいろなオプション機能があります．
以下は，オプション部分とそれにより表示される画像を示したものです．
|
|
|
| emathの利用 |
作成した画像を文章混じりのプリントに取り入れるには，
「emath」のmawarikomi環境やedaenumerate環境を利用するとよいでしょう．
具体的な利用の仕方は，
「emathの利用法」のページを見てください．
ここでは，利用例のみを示します．
|
|
|
| epslatexによる出力 |
gnuplotの中で日本語を使用できても，
それをeps保存すると文字化けしてしまいます．
その場合は，「eps」ではなく「epslatex」を指定して出力すると，
出力されたファイルに対して日本語を使用することができます．
前項までに利用してきた放物線 \(y=x^2-2x\) を描画(plot)した上で，
次の指定を行います．
出力された「sample_j.tex」の内容を理解しようとする必要はありません． このファイルの前半では，種々の定義や諸設定が行われてます． グラフ画面に関する内容は， 後半にある￥begin{picture}, ￥end{picture}で囲まれている部分に 書き込まれています．＄-2＄などの部分は外枠に目盛りを書き入れています． ￥putで座標を指定しているので， 目盛りが書き込まれている箇所の位置が分かります．
なお，次のようにする方法もあります．
|
