MePoTeXを活用して，図形とグラフを究めよう！
(注1) MathJaxを使用しているので、 スマホでは表示に時間がかかることがあります。
(注2) 図やコードが文章に被って表示されるときは「再読み込み」して下さい。
(注3)モバイル利用(Android)でのメニュー選択は、 SiteMapを利用するか、 「長押し」から「新しいタブを開く」を選択してください。
| ■MePoTeXによる図形やグラフの作成法 [Map] |
|
|
|
|
|
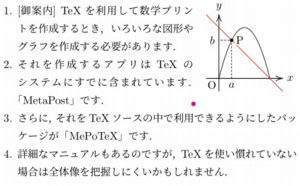
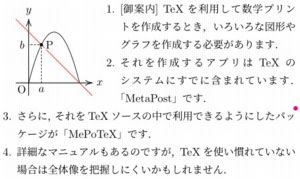
[御案内] TeXを利用して数学プリントを作成するとき，
いろいろな図形やグラフを作成する必要があります．
それを作成するアプリはTeXのシステムにすでに含まれています．
「MetaPost」です．さらに，それをTeXソースの中で利用できるようにした
パッケージが「MePoTeX」(概要)です．詳細なマニュアルもあるのですが，
TeXを使い慣れていない場合は全体像を把握しにくいかもしれません．
そこで，ここでは，TeXを使い始めた方を念頭に， MePoTeXを用いた図形やグラフの作成方法について解説します． ただし，TeXのインストールはすでになされており， TeXによる通常文書は作成できるレベルにあることを前提とします． emathと類似したコマンドで 曲面の描画まで行うことができ、 図形をGhostscriptを経由しないEPSファイル(MPS)で保存することができます。
|
|
|
| ■いろいろな応用操作 |
|
(注) Web上での表示の都合上、 空白は全角を使用しています。 以下のコードをコピーして実行するときは、 半角の空白かtabで置き換えて実行してください。 | ||||||||||||||||||||||||||||||
| 複素数の計算 | ||||||||||||||||||||||||||||||
|
MetaPostでpair宣言された2次元ベクトルは、
平面上の点の座標やベクトルの成分を表すだけではなく、
複素数として扱うこともできます。
初字「z」から始まる変数は、
pair宣言をしなくても
そのような変数として扱うことができます。
たとえば、z1=(a,b)、z2=(c,d) とするとき、 和は z3=z1+2 により求められます。 積を z4 とすると、積は「z4=z1 zscaled z2」により計算されます。 商は、MetaPostは連立1次方程式を 解くことができることを利用します。 z5=z2/z1 とすると、z5は「z2=z5 zscaled z1」により定まります。 MetaPostは、 この式から定まる成分の連立1次方程式を 自動的に解いて z5 を求めます。 以下は、\(\small z1=3+i,~z2=2+3i\) の場合を計算しています。 \(\small z3=z1+z2=5+4i\)、\(\small z4=z1 z2=3+11i\)、 \(\small z5=\frac{z2}{z1}=\frac9{10}+\frac7{10} i\) です。
| ||||||||||||||||||||||||||||||
|
[A]では、最初に長さと角度(度)を納める変数を宣言して、
z1, z2を単位付きで定義しています。
そのあとで、和 z3 を計算し、積 z4 と商 z5 は
単位「w」を省いた式で定義しています。
ここでは、w=h=1cm です。「1cm」といっても、
実際には「cm」は変数であり、1cm=28.34645bp であるようです。
MetaPostでの長さの単位は「bp」(ビッグポイント)が用いられているので、
単位付きの計算は、
実際には28倍した値で計算されています。
たとえば、単位をつけたz2の長さは、 \(\small \sqrt{2^2+3^2}=\sqrt{13}\) ではなく、 \(\small \sqrt{(2\cdot 28.3\cdots)^2+(3\cdot 28.3\cdots)^2}\)(bp) が計算され、場合によってはオーバーフローになります。 このような値は単位を省いて計算する必要があります。 単位は、描画の直前につけるように留意する必要があります。 z4とz5には単位「w」をつけていないので、 [B]では、描画するときに「w」をつけています。 また、積や商を原点z0と結ぶ線は、 そのまま描画すると長くなりすぎるので単位ベクトルにして繋いでいます。 [C]では長さを求めています。z1,z2,z3 は単位付き、z4, z5は単位無しなので 注意してください。 z1の長さは、 w で割って単位を省いて計算しています。 [D]では「angle」により角度が「度」で求まります。 [E]で求めた座標や数値を保存し、[F]で「\UseNumeric」を利用して値を表示 しています。表示された数値を見ると、 \(\small |zw|=|z| |w|\), \(\small \arg(zw)=\arg(z)+\arg(w)\) など、 複素数の性質が満たされていることが分かります。 なお、値を表示する箇所では、開始位置が揃うように微妙な調整をしています。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| picture値変数 | ||||||||||||||||||||||||||||||
|
MetaPostで扱うことのできる変数に
「picture」で宣言される変数があり、画像を変数に格納することができます。
「xdraw」や
「xfill」は、
MetaPostのもともとの機能である「draw」や「fill」を、
いろいろなオプションを簡単に追加できるように
「みなも」氏によりマクロ化されたものです。
それによりいろいろな図形が描かれますが、
それは「currentpicture」というデフォルトで定まっているpicture値変数に
書き込まれています。しかし、MetaPostの機能では、
任意のpicture値変数に書き込むことはできません。
MePoTeXでは、任意のpicture値変数に書き込むことができるように
機能が拡張されています。picture値変数を「pct」とするとき、
「drawpic(pct) z1--z2;」「xfillpic(pct)(red) z1--z2--z3--cycle;」
などのように利用します。( )内のオプションは、xdraw( )、xfill( )
の場合と同じものが利用できます。
picture値変数を宣言するには、\sendMP内で「newpic(pct);」とします。 これにより、「picture pct;」という変数宣言と、 「pct:=nullpicture;」という初期化が行われます。 単に変数宣言だけでは書き込むことはできず初期化する必要があるので、 「newpic(pct);」の形で利用するのがよいでしょう。 複数のpicture値変数を用いたいときは、 「newpic(pct)("1upto3");」あるいは「newpic(pct)("1,2,3");」 のように宣言します。これにより、pct1, pct2, pct3の宣言と 初期化が行われます。 以下に、簡単な利用例を示します。
| ||||||||||||||||||||||||||||||
| 最初に点を繋いだパス値を定義します。 pth1は左下の正方形、pth2はその隣の右下の正方形、 そしてpth3は上にある長方形です。 塗りつぶしを行うには「--cycle;」で閉じる必要があります。 次に、宣言したpicture変数に書き込みます。 pct1にはpth1を描画、pct2にはpth2を赤色で塗りつぶして描画、 そしてpct3には斜線塗りと外枠を青色にして描画しています。 picture値変数に書き込んだだけでは実際には表示されません。 描画したものを見えるように表示するには「draw pct1;」などとします。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| 線形代数 | ||||||||||||||||||||||||||||||
線形代数で学ぶ線形変換はベクトルに行列をかけることで得られる変換です。
授業で扱うときは、
平面上の正方格子模様が
どのように変換されるかを示したいところですが、
単純ではあっても、その図を作成するのは面倒です。
しかし、MetaPostではアフィン変換の
成分を表す変数があります。
その変数を利用すると、正方格子の変形を簡単に行うことができます。
以下では、正方格子がどのように変換されるかを、
\[\small \begin{pmatrix}x'\\ y'\end{pmatrix}
=\begin{pmatrix}2&1\\ 1&1\end{pmatrix}
\begin{pmatrix}x\\ y\end{pmatrix}\]
の場合について例示します。
| ||||||||||||||||||||||||||||||
|
MPpic環境を開くときの範囲は、\(\small -8\leqq x\leqq 4,~-4\leqq y\leqq 6\)
に設定しました。例示した変換では格子模様が右斜め方向に
大きく伸びるので、その図形全体が表示されるように調整したためです。
[A]では、\(\small -3\leqq x\leqq 3\)、\(\small -3\leqq y\leqq 3\) の範囲で格子を描画しています。 MPpic環境で指定した領域内の一部に格子を描画するときは、 xmin, xmax などを指定する必要があります。 この段階で正方格子が描画され、「currentpicture」という デフォルトのpicture値変数に格納されます。 [B]ではパス値とtransform値の宣言をして、 [C]でpicture変数の宣言と初期化をおこなっています。 [D]では、tarnsform値「t」の定義を行い、 [E]では、[A]で正方格子が描画されたcurrentpictureを [C]で定めたtransform値で変換して、 [B]で宣言したpicture値変数「pct」に納めています。 [F]では1辺が1cmの正方形をパス値変数「pth0」に格納します。 以上のもとで、[G]では、正方形pth0と、それを変換した図形pth1を描画します。 そして、最後に[H]では、 [A]での正方格子を変換した[E]のpctを描画しています。 [D]の部分を変更するだけで、いろいろな行列で試してみることができます。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| 微分方程式 | ||||||||||||||||||||||||||||||
|
勾配場 1階の微分方程式が \(\small y'=\dfrac{g(x,y)}{f(x,y)}\) の形で表されていると、 その解が分からなくても 指定した点 \(\small (x,y)\) を通る解曲線の接線の傾きは右辺を 計算すれば簡単に分かります。そこで、平面上の各点で右辺の値を求めて 対応する接線を短い線分で描けば、解が分からなくても解曲線の大まかな様子を 知ることができます。そのような図は勾配場と呼ばれます。 MePoTeXには、この勾配場を描くマクロとして「drawVectorField」があります。 6つの引数を持ち、 「drawVectorField(1)(2)(3,4,5,6)」の形で使用します。 線分ではなく矢印を置くこともできます。 それぞれの引数は、次のような内容です。
| ||||||||||||||||||||||||||||||
以下に、幾つかの典型例を示します。
\(\small (-t,s)\) の部分を変更するだけです。
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
ベクトル場 \(\small x, y\) が媒介変数 \(\small u\) を用いて 連立微分方程式で \[\small \begin{align*}&\frac{dx}{du}=f(x,y)\\ & \frac{dy}{du}=g(x,y)\end{align*}\] と表されていると、解が分からなくても 点 \(\small (x,y)\) における接線ベクトルが定まり、 媒介変数 \(\small u\) の増加する方向に矢印がつきます。 このように、点の進む方向に矢印をつけた図はベクトル場と呼ばれます。 MetaPostでは独立変数として \(\small s, t\) が使用されるので、 ここでは媒介変数を \(\small u\) としています。 このとき、解曲線の接線の傾きは \[\small \frac{dy}{dx}=\dfrac{dy/du}{dx/du}=\dfrac{g(x,y)}{f(x,y)}\] により求められるので、 この場合も「drawVetorField」を利用することができます。 また、定数係数斉次2階微分方程式 \(\small y''+py'+qy=0\) の場合は、 \(\small y'=z\) とおくと、\(\small y''=z'=-pz-qy\) となるので、\(\small x\) を媒介変数とした連立微分方程式 \[\small \frac{dy}{dx}=z,~\frac{dz}{dx}=-qy-pz\] となり、変数を置き換えると \[\small \frac{dx}{du}=y,~\frac{dy}{du}=-qx-py\] と同じことです。 | ||||||||||||||||||||||||||||||
以下に、2階微分方程式の場合に幾つかの例を示します。
この場合は接線ベクトルで矢印がつくので、
6番目の引数を「4pt」にしています。
ただし、\(\small (y, y')\) に関する場が描画されており、
解曲線自体の接線方向ではないので注意が必要です。
このような平面は「相平面」と呼ばれています。
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
定数係数連立線形微分方程式 周知のように、連立微分方程式が \[\small \frac{d}{du}\begin{pmatrix}x\\ y\end{pmatrix} =\begin{pmatrix}a& b\\ c& d\end{pmatrix} \begin{pmatrix}x\\ y\end{pmatrix}\] の形で表される場合、解の様相は係数行列の固有値の取り方により 分類されます。 以下に幾つかの例を示します。 この場合は、解曲線の接線方向の矢印になります。
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
解曲線 ■勾配場と解曲線 微分方程式の解曲線は、 その解を解析的に求めてグラフ表示すれば描くことができます。 たとえば、ロジスティック方程式 \(\small y'=y(1-y),~y(0)=0.5\) の解は \(\small y=\dfrac{e^{x}}{1+x^{x}}\) で表されますが、 勾配場と重ねて描くと次のようになります。 下記では、\(\small y\) 軸方向を3倍して描画しています。
| ||||||||||||||||||||||||||||||
下記は、\(\small y''-2y'+y=0\) について \(\small (y,y')\)
に関する相平面と、\(\small y(0)=0, y'(0)=1\) を満たす解の軌道です。
一般解は \(\small y=(a+bx)e^{x}\) なので、
与えられた初期条件を満たす特殊解は \(\small y=xe^{x}\) です。
\(\small y'=(1+x)e^{x}\) であるので、相平面では
\(\small (xe^x, (1+x)e^x)\) の軌道が描かれます。
媒介変数の場合の「kansuP」を利用して描いています。
| ||||||||||||||||||||||||||||||
| ここで、冒頭にある「\mptNumSys{double}」というコマンドは、 倍精度で計算することを指定しています。 MetaPostの「numeric」で宣言される数は、 デフォルトでは4096未満で、1/65536 の整数倍で表される数です。 デフォルトのままで大きな数を計算させると あっという間にオーバーフローしてしまうので、 数が大きくなりそうなときは「\mptNumSys{double}」を指定して、 倍精度で計算するようにしておく必要があります。 ここでは指数関数が出てくるので倍精度にしています。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
数値解法(1階・2階微分方程式) 微分方程式の解を解析的に求めることが難しい場合は、 解を近似的に数値解で求めることになります。 そのような方法としては、 オイラー法やルンゲ・クッタ法がよく知られています [参照]。 MePoTeXのVer4.50では、1階・2階の場合の微分方程式を ルンゲ・クッタ法で解くマクロが新設されました。 | ||||||||||||||||||||||||||||||
|
■ 1階微分方程式 1階は \(\small \dfrac{du}{dt}=F(u,t)\) の場合を考えます。 書式は、次の通りです。 rungekutta(F(u,t))(始点, 終点, 刻み幅)(初期値) 始点、終点、刻み幅には、それぞれ \(\small t\) の値をいれます。 始点を与える \(\small t\) での値が初期値です。 これにより、解曲線のパスが得られます。 たとえば、勾配場で例示した ロジスティック曲線のパスは、
\(\small t\ge 0\) rungekutta(u*(1-u))(0, 4, 0.2)(0.5)
| ||||||||||||||||||||||||||||||
|
■ 2階微分方程式 2階は \(\small \dfrac{d^2u}{dt^2}=G(u,u',t)\) の場合を考えます。 ただし、\(\small u'\) のままMetapostに引き渡すことができないので、 \(\small v\) におきかえて利用します。 書式は、次の通りです。 rungekutta(G(u,v,t))(始点, 終点, 刻み幅)(初期値) 始点、終点、刻み幅には、それぞれ \(\small t\) の値をいれます。 始点を与える \(\small t\) での値が初期値です。 ただし、2階なので、始点を \(\small t_0\) とすると \(\small u(t_0), u'(t_0)\) の値を与えることになります。 たとえば、勾配場で例示した 2階微分方程式は \(\small y''=2y'-y\) であり、 初期値を \(\small y(0)=0, y'(0)=1\) とすると、
\(\small t\ge 0\) rungekutta(2*v-u)(0, 2, 0.2)(0, 1)
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
数値解法(n質点系) MePoTeXには、\(\small n\)質点系の運動方程式を ルンゲ・クッタ法で解くマクロ「RungeKutta」もあります。 ここでは、このマクロの利用法を解説します。 | ||||||||||||||||||||||||||||||
|
■ n 質点系の運動方程式 [参照] n 質点系の運動方程式は、 \(\small n\) 個の質点の質量を \(\small m_i\)、 位置ベクトルを \(\small \mathbf{q}_i\) とするとき、\(\small i\) 番目の質量に働く外力を \(\small \mathbf{F}_i\)、 他の質点から作用する力の和を \(\small \sum_{k\neq i}\mathbf{G}_{ki}\) と すると、\(\small i=1,2,\ldots,n\) とするとき、次の式で表されます。 \[\small m_i\dfrac{d^2\mathbf{q}_i}{dt^2}(t) =\mathbf{F}_i(t)+\sum_{k\neq i}\mathbf{G}_{ki}(t)\] この式は、\(\small \dfrac{d\mathbf{q}_i}{dt}=\mathbf{p}_i\) とおくと、 次のような連立微分方程式で表されます。 \[\small \begin{align*} &\dfrac{d\mathbf{q}_i}{dt}=\mathbf{p}_i\\ &m_i\dfrac{d\mathbf{p}_i}{dt}=\mathbf{F}_i(t)+\sum_{k\neq i}\mathbf{G}_{ki}(t) \end{align*}\] MePoTeXのマクロ「RungeKutta」では、これを一般化して、 \[\small \begin{align*} &\dfrac{d\mathbf{q}_i}{dt}=\mathbf{p}_i\\ &\dfrac{d\mathbf{p}_i}{dt}=f_i(\mathbf{q}_1,\mathbf{q}_2,\ldots, \mathbf{p}_1,\mathbf{p}_2,\ldots,t) \end{align*}\] の形の場合の数値解を求めることができます。次の形で利用します。 \[\small {\rm RungeKutta}(1)(2,3,4)(5)(6)(7)\] それぞれの引数は、次のような内容です。
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
■ 1質点系の運動 ここでは、MePoTeXのマニュアル[1] (p70, 図122)で取り上げられている1質点系の運動の例を紹介します。 これは、距離が \(\small 2L\) だけ離れた2つの梁に、 同じバネ定数 \(\small k\) を持ち自然長が \(\small L_0\) のバネの1端を 固定します。そして、もう一方のバネの1端を1つの質点と繋ぎます。 そして、それを特定方向に引っ張ったときの質点の描く軌跡を 求めるものです。
| ||||||||||||||||||||||||||||||
| 上段の図は、 \(\small t\) の範囲を \(\small 0\sim 8\pi\) とした場合、 下段は \(\small 0\sim 16\pi\) の場合です。 MePoTeXのパッケージをダウンロードすると、 この質点の動きをバネの動きとともに 429頁のパラパラ漫画にしてPDFファイルを生成するソースファイルが登録されています。生成されるPDFファイルは「こちら」です。 プレゼンテーションモードでページ送りキーを押し続けてみて下さい (「みなも」さんより公開の許可をいただきました)。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
■ ローレンツアトラクター ローレンツアトラクターは気象学者ローレンツにより発見されたもので、 3次元空間で次の微分方程式で表される解軌道です。 \[\small \begin{align*} &\dfrac{dx}{dt}=a(y-x)\\ &\dfrac{dy}{dt}=bx-y-xz\\ &\dfrac{dz}{dt}=xy-cz \end{align*}\] 式から分かるように、これは非線形の連立微分方程式です。 ローレンツは、 具体的には \(\small a=10\)、\(\small b=28\)、\(\small c=8/3\) の場合を 検討しています。具体的な気象現象から立式しているにもかかわらず、 初期値を与えて解曲線を描かせると周期性は見られず、 さらには初期値の微妙な変化で軌道が大きく異なります。 きちんとした式で表現できているのに結果が見通せないことは、 当時の科学界に大きな衝撃を与えました。 この軌道はローレンツアトラクターと呼ばれ、 カオス現象が発見された頃の先駆的なものです。 [ 参照1、 参照2、 参照3、 参照4、 参照5、 参照6 ] MePoTeXのマクロ「RungeKutta」を利用すると、 この連立微分方程式の解を求めてその軌道を描画することができます。 微分方程式の右辺の式を引き渡すため、 空間ベクトル \(\small (x,y,z)\) を \(\small (p1,p2,p3)\) とするとき、 このベクトルの個々の成分 p1, p2, p3 の満たす1階の 3元連立微分方程式を考えます。 \[\small \begin{align*} &\dfrac{dp_1}{dt}=a(p_2-p_1)\\ &\dfrac{dp_2}{dt}=bp_1-p_2-p_1p_3\\ &\dfrac{dp_3}{dt}=p_1p_2-cp_3 \end{align*}\] この関係を「RungeKutta」で処理すると、 解が引数(7)で 指定するパス変数(たとえば「pth」) に格納され、 p1, p2, p3 の軌跡は それぞれ pth[-1], pth[-2], pth[-3] に格納されます。 たとえば、pth[-1] は、 p1 と対応する t を成分に含むペア型変数を 繋いで得られるパスです。 同じ時刻 t の座標をまとめて空間座標 (p1,p2,p3) を得て、 その点の時刻を変えることで得られる軌跡が求める解軌道です。 つまり、得られた3個のパスから座標成分だけを取り出して一つにまとめて、 3次元空間の点として再構成します。 しかし、MetaPostには、空間の点を繋いでパスを構成する機能がありません。 そこで、MePoTeXでは、空間の点として再構成した点を 射影して平面上の点とします。そして、 その平面上の点を繋ぐことでパスを構成しています。 それを行うマクロが「projpath」です。 「projpath(pth[-1],pth[-2],pth[-3])」とすることで、 空間における解曲線の点を平面に射影した点のパスが得られます。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
以上をもとに、\(\small a=10\)、\(\small b=28\)、\(\small c=8/3\) の
場合の軌道を求めると、次のようになります。
マニュアル[1]
の図124(p72)を簡略化したもので、
時間間隔を 0.01 として、\(\small 0\sim 10\) の範囲の軌道です。
| ||||||||||||||||||||||||||||||
|
ここでは、[A]により使用する係数を変数宣言して値を代入しています。
[B]では、マクロ「RungeKutta」の引数を指定します。
マニュアル[1]の図124(p70)では、
初期値を \(\small (6,9,20)\) としています。
[C]では、視点を
\(\small (3,0,1)\)方向に指定しています。
\(\small yz\)平面への射影状況が分かります。
[D]では、得られた p1,p2,p3 の解から空間の点 (p1,p2,p3) を構成して、
それを「projpath」を利用して平面に射影して繋いで
パス値「ptha」を作成しています。
その上で、[E]で軌道「ptha」を描画し、[F]で座標軸を書き入れています。
2番目の図は、視点を \(\small (0,3,1)\) 方向とした場合です。 \(\small xz\) 平面への射影状況が分かります。 3番目は、視点を \(\small (1,1,4)\) とした場合です。 上から覗いた感じになります。 最初の図は、蝶の羽のように見えなくもありません。 左側と右側を「不規則に」行ったりきたりします。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
パラパラ漫画 このローレンツアトラクターの軌道を， 「パラパラ漫画」にしてみましょう． コマ数を $\small n$ とするとき， 前述のコードを「\mptparapara{n}」と「\repeat」で囲って， 「\sendMP」内で「\mptgetkoma{n}」によりコマ数を受け取り， その値をもとに任意コマのグラフを描画するように修正するだけです． 下記では，$\small [0, 10]$ の区間を100分割し， $\small tm=\dfrac{i}{100}\cdot 10$ とするとき， $\small i$ コマ目は $\small [0, {\rm tm}]$ の範囲での グラフを描画するように指定しています． $\small i$は明示的には示されていませんが， 「tm:=(n/100)[0,10]」とすることで， tm の値が 0 から n まで自動的に変わり， 計(n+1)枚のページが生成されて1つのPDFにまとめられます． 大量の画像ファイルが生成されるので， 保存フォルダーは「\mptSaveDir」 を利用して指定しておきます．
| ||||||||||||||||||||||||||||||
|
PDFで表示するとき，プレゼンテーションモード，
つまり「表示」の仕方は「単一ページ表示」とし
「ズーム」は「ページレベルにズーム」としておくと，
ページ送りキーを押し続けるとパラパラ漫画風に表示されます．
このように，MePoTeXを利用すると，
TeXの中でローレンツアトラクターを描画でき，
さらには，そのパラパラ漫画化までが簡単にできることになります．
生成されたPDFを下記に登録しておきます。 頁数を増やすときは、「tm:=(n/100)[0,10]」の「100」と「10」の箇所も 同時に修正する必要があります。 500頁にしたら、400頁を超えたあたりでオーバーフローで止まってしまいました。 400頁まではうまくいきますが、2時間近くかかりました。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
| 統計グラフ | ||||||||||||||||||||||||||||||
|
MetaPostは統計ソフトではありませんが、
図の作成に必要な値が与えられると、
いろいろなグラフを描画することができます。
| ||||||||||||||||||||||||||||||
|
ヒストグラム ヒストグラム(柱状グラフ)は、データの分布の様子を棒グラフで示すものです。 必要な値は、柱の横幅と高さです。柱の幅を共通とすると、 その柱を配置するための位置(階級値)も指定する必要があります。 高さは、度数、相対度数、確率密度の場合がありますが、 それは縦軸の目盛りで調整できます。 以上のことを踏まえて、柱の幅は「HisWd」、 ヒストグラムは「Histogram(階級値, 高さ)(色)」で指定します。 実際に描画するには、生データから度数分布表を作成しておいて、 その値をもとに個々のヒストグラムを記述することになります。 たとえば、次のような度数分布表を考えます。
Histgram(階級値,度数)(属性列) の形で指定します。 属性列では、1個の数値か、2個のcolor値を指定できます。 数値の場合は柱の枠の太さを指定でき、color値の場合は枠内と枠線の色を 指定できます。
| ||||||||||||||||||||||||||||||
|
ここでは、縦横の範囲が大きいので、
単位あたりの長さを <0.07cm, 0.2cm> として詰めています。
[A]では、指定した範囲の一部領域に対する格子描画なので、
その範囲を xmin などを利用して指定します。
[B]では、カラー値変数の宣言をして、
具体的な色を HSB形式で
指定しています。この指定はマニュアル[1]
の図93(p59)の指定を
そのまま利用しています。
[C]では個々のヒストグラムを指定します。一部のヒストグラムでは、
内部の色や枠の色を変えています。
[D]は、一つの柱を(意味はありませんが)斜線塗りにしました。
「Histogram」のコマンドでは対応できないので、
xfill()を利用して描画しています。
[E]では縦線を引き、[F]では座標の数値を書き込んでいます。
相対度数で示したいときは、「度数」の箇所を相対度数で指定します。 小数値で指定してもよいですが、面倒なので全度数で割る形で指定した方が 簡単ですみます。ただし、縦軸は最大でも 1 以内にする必要があるので、 縦軸の単位や y 座標について修正する必要があります。 縦軸の刻み幅は小数値になりますが、 MetaPostの扱うことのできる小数は 1/65536 の整数倍の数値です。 あまり小さい数を扱う必要があるときは \mptNumSys{double} を指定して 倍精度にしておいた方が良いでしょう。 また、座標軸の箇所に表示するときは、桁数を丸めて表示します。 その場合の丸める小数点以下の桁数は、 「\mptRound{桁数}{変数}」で指定することができます。 以下は、相対度数で描画した場合です。 桁数は、{\ycoord}の前の ( ) 内で指定します。
| ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
散布図 散布図の描画を行うマクロは「ScatterPlot」であり、 「ScatterPlot(描画命令)(点列)」の形で利用します。 「点列」は、散布する点の座標 (a,b) を「,」で区切って指定します。 描画命令は、指定した点にどのような図形を書き込むかを指定します。 その図形は、原点を中心とした path値で指定します。 たとえば、原点を中心とした半径 2pt の円を青 く塗りつぶして配置するには、 描画命令は「xfill(blue) circle(origin,2pt)」となります。 下図は、たとえば補習該当者を赤の三角印にしています。
| ||||||||||||||||||||||||||||||
| [C]での赤三角は、最初にパス値変数の宣言を行い、 底辺の2点 z0, z1 の座標を定義します。 その上で、もう一つの頂点 z2 を、 3辺の比が \(\small 1:1:1\) の三角形の頂点として定めます。 そして、頂点を結んで得られる三角形を pth とした上で、 その三角形を「xfill(red) pth」により赤で塗りつぶしています。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
箱ひげ図 箱ひげ図は、データの分布の様子を、 最小値・最大値と3つの四分位数を用いて図示したものです。 箱ひげ図を描くマクロは「HakoHige」で、次のような書式です。 HakoHige(min,Q1,Q2,Q3,max,位置)(属性列) min と max はデータの最小値と最大値、Q1〜Q3は第1四分位数から第3四分位数、 そして箱ひげ図を横に描いた場合の縦方向の位置です。 そこで指定した値に「h」をつけた位置に図が描かれます。 属性列では、numeric値が最大3個、color値は最大2個指定できます。 数値の場合、1つ目はひげの太さ、 2つ目は横置きにした場合の端点(最小・最大)の縦の長さの半分の値、 3つ目は箱の線の太さです。 color値は、1つ目は内部の色、2つ目は枠の色です。たとえば、下記のようになります。
| ||||||||||||||||||||||||||||||
| 上記では、高さ「1h」の箇所に下の図が、 「3h」の箇所に上の図が描かれています。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
外部ファイルの利用 分析するデータから基本統計量が求まっているときは、 前述のような形でヒストグラムや箱ひげ図を描くことができます。 一方で、データ数が多い場合の散布図は、 その座標をいちいち書き込むのは面倒です。 そのような場合には、データを外部ファイルとして用意しておいて、 それを読み込むような形で利用することができます。 | ||||||||||||||||||||||||||||||
|
■外部ファイルの読み込み 統計データはcsv形式とすることが多いので、 ここでは CSV形式(カンマ区切り)による数値データの読み込みで利用します。 それを行うマクロは「ReadCSV」です。 書式は、次のような形です。 タブ区切りのデータでは「ReadTSV」を利用します。 zz:=ReadCSV("data.csv")(v) CSVファイルは、カンマ区切りの(数値)データ行列です。 上記により、v にその行列データが格納され、 その行数と列数がペア型変数 zz に「(列数, 行数)」の形で返され、 データ行列の (i,j) 成分は、v[j][i] の形で参照することができます。 したがって、v[j] だけで j列が得られます。 行と列の指定が逆になっていることに注意して下さい。 zz からは、「xpart zz」により列数を、「ypart zz」により行数を 取り出すことができます。xpart(zz) などとしてもかまいません。 | ||||||||||||||||||||||||||||||
|
■外部ファイルを利用した散布図 「ReadCSV」を利用して、 散布図のときのデータを 「samplc.csv」 として保存して読み込んでみましょう。 このファイルは、2列からなる10個ずつのデータ、 すなわち (10,2)型の行列です。
| ||||||||||||||||||||||||||||||
|
上記のコードでは、
「ypart(zz)」により行数を取り出して nn とし、
ii を 1 から nn まで変えながら、
座標が (v[1][ii], v[2][ii]) の箇所に青丸を配置しています。
元データでいうと、x 座標は (ii,1)成分、y 座標は (ii,2)成分です。
青丸は、原点(orijin)を中心とする半径2ptの円を塗りつぶしたものです。 その円を読み取った座標の箇所に「shifted」で移動すれば、 ScatterPlotを利用しなくても散布図を描くことができます。 ただし、その際は単位の w, h をつける必要があります。 グリッドや軸の数値の描画は、散布図の箇所の [A][D]と同一です。 \sendMP の外側(前半でも後半でもかまわない)で記述します。 | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
|
■回帰直線 読み込んだデータ「v」から、 平均・標準偏差・共分散を求めて回帰直線を描画することもできます。 2つの変量の平均・標準偏差・共分散・相関係数を求めるマクロは「MvSdCov」で、 MvSdCov(配列1)(配列2)(番号列) の形で使用します。 これにより、2つの変量の平均・標準偏差・共分散・相関係数が得られます。 全部で 6 個の値が返されるので、 transform宣言をした変数で 受け取る必要があります。 たとえば、v をデータ行列として、 2つの変量 \(\small x, y\) を1列目と2列目とするとき、 S を transform宣言した変数とするとS:=MvSdCov(v[1])(v[2])(1 upto ypart(v)) により各変数の統計量が得られ、 個々の具体的な値は次のようにして取り出すことができます。 3番目の引数は、統計量を計算するデータの範囲を指定しています。 たとえば、(1 upto 10) などを指定すると、 最初の10個のデータについて計算されます。ただし、統計計算はかなり大きな桁数になったりするので、 これらのマクロを使用する\sendMPの前では 倍精度の指定(\mptNumSys{double})をした方が安全でしょう。 なお、倍精度の指定を行う場合、変数に「e」は使用できません。
| ||||||||||||||||||||||||||||||
|
■平均と標準偏差 2変量ではなく、1変量の平均や標準偏差を求めるマクロは「MvSd」です。 たとえば、「numeric v[];」として v を1次元配列として宣言し、 ss と zz をペア宣言として 「zz:=ReadCSV("data.csv")(v)」によりデータを読み取ったとします。 v のデータ数を nn とすると、 ss:=MvSd(v)(1 upto nn) により、ss には v の平均と標準偏差が「(平均, 標準偏差)」の形で返されます。 「numeric v[][];」として v を2次元配列とした場合は、 v[i] で i 列を参照できるので、nn を v[i] のデータ数とするとss:=MvSd(v[i])(1 upto nn) とすることで、i 列の平均は xpart(ss)，標準偏差は ypart(ss) により得られます。 |
