|
(注) Web上での表示の都合上、
空白は全角を使用しています。
以下のコードをコピーして実行するときは、
半角の空白かtabで置き換えて実行してください。
|
|
描画の小技 |
|
[参照] \mptDrawGrid、
\mptXaxis、
\mptLabel、
\sendMP、
xdraw
|
軸への垂線等
|
|
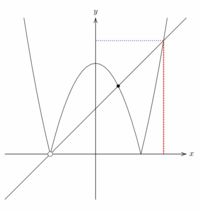
極値を取る点や交点から座標軸に垂線を下ろすには、
\sendMP内で「xdraw()」により「Pline, Pxline, Pyline」を実行します。
指定した点から座標軸に垂線を引くことができます。
「xdraw」を利用するので、線種や色を指定することもできます。
下図では、個々の座標軸に別々に垂線を引いて、
線種や色を指定しています。
Plineを利用すると、2つの座標軸に同時に垂線が引かれます。
特定の点を白丸にしたいときは「tanten(座標)」、
黒丸にしたいときは「Tanten(座標)」とします。
丸の半径を変えるには「(pt数)」を後に続けて書きます。
下記では、白丸を少し大きくしています。
数値や文字を入れるには「\mptLabel」を利用します。
-
\begin{MPpic}<1cm>(4|4,6|2)
% 座標軸の描画
\mptXaxis[l]
<1mm,0mm>{$x$}
\mptYaxis[b]
<0mm,1mm>{$y$}
% グラフの描画
\sendMP{
xdraw() ClipPATH(kansu
(abs(t*t-4))(-4,4,40));
xdraw() kansu(t+2)
(-4,4,10);
xdraw(1pt,hasen(),red)
Pxline(3w,5h);
xdraw(1pt,tensen(),blue)
Pyline(3w,5h);
tanten(-2w,0)(3pt);
Tanten(1w,3h);
}
\end{MPpic}
-
|
|
水平線・垂直線
|
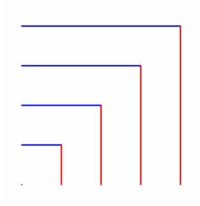
水平線や垂直な線を引くには、
\sendMP内の「xdraw()」の後で「Hline, Vline」を利用します。
領域全体に引くこともできれば、特定の区間にだけ引くこともできます。
たとえば、\(\small y=b\) の箇所で水平な線を引くには、
「xdraw Hline(b)()()」とします。区間を指定したいときは、
後半の2つの括弧に値を入れます。単位の w, h をつける必要はありません。
Vlineの場合は、\(\small x\) 座標に関して同様にします。
-
\begin{MPpic}<1cm>(4,4)
% グラフの描画
\sendMP{
for n=0 step 1 until 4:
xdraw(1pt,blue)
Hline(n)()(n);
endfor;
for n=0 step 1 until 4:
xdraw(1pt,red)
Vline(n)()(n);
endfor;
}
\end{MPpic}
-
|
|
グラフの交点
|
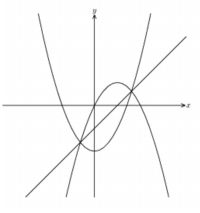
グラフの交点を求めるには、「InSecPoint」(InterSectionPointの略)を利用します。
2つの陽関数の交点、陽関数と直線、直線と直線の交点を求めることができます。
書式は、次のような形です。
関数の箇所には、関数の式を \(\small t\) の式で指定します。
直線上の2点には、具体的な2点を「,」で区切って指定します。左端と右端には、
交点が1つだけであるような区間を指定します。
- InSecPoint(関数1)(関数2)(左端,右端,分割数)
- InSecPoint(関数)(直線上の2点)(左端,右端,分割数)
- InSecPoint(1次関数)(1次関数)()
- InSecPoint(直線上の2点)(直線上の2点)()
-
\begin{MPpic}<1cm>(4|4,4|4)
% 座標軸
\mptXaxis
<1mm,0mm>{$x$}
\mptYaxis
<0mm,1mm>{$y$}
% グラフ描画
\sendMP{
path gra,grb;
gra=kansu(t*t-2)
(-4,4,40);
grb=kansu(-t*t+2*t)
(-4,4,40);
xdraw() ClipPATH(gra);
xdraw() ClipPATH(grb);
z.A=InSecPoint(t*t-2)
(-t*t+2*t)(-4,0,20);
z.B=InSecPoint(t*t-2)
(-t*t+2*t)(0,4,20);
xdraw() ExtLine(z.A,z.B);
}
\end{MPpic}
-
|
上記では、最初にパス変数を用意して、
2つの関数 \(\small t^2-2, -t^2+2t\) のグラフを記録させて、
ClipPATHを利用して
指定区域をはみ出さないように描画します。
次に、左側の交点を z.A 、右側の交点を z.B として、
「ExtLine」で2点を結ぶ直線を描いています。
「ExtLine(点,点)」は、2点を結ぶ直線を指定区域内に描きます。
|
|
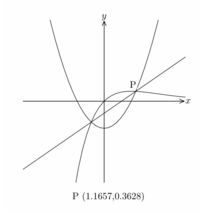
交点は、多項式でなくても求めることができます。
下記では、\(\small t^2-1, te^{-t}\) の交点を求めています。
交点の座標の表示のさせ方は次の項目を参照してください。
この機能をグラフを描画させないで利用すると、
要するに超越方程式の近似解を求めることができるということです。
-
\begin{MPpic}<1cm>(3|3,3|3)
% 座標軸 (中略)
% グラフの描画
\sendMP{
path gra,grb;
gra=kansu(t*exp(-t))
(-2,4,40);
grb=kansu(t*t-1)(-3,3,40);
xdraw() ClipPATH(gra);
xdraw() ClipPATH(grb);
z.A=InSecPoint(t*t-1)
(t*exp(-t))(-3,0,20);
z.B=InSecPoint(t*t-1)
(t*exp(-t))(0,3,20);
xdraw() ExtLine(z.A,z.B);
SavePointName(z.B);}
\mptLabel{z.B}[b]
<-1mm,1mm>{P}
\mptLabel{(-w,-3.5h)}
{P~\UseNumeric{z.B}}
\end{MPpic}
-
|
|
数値の表示
|
MePoTeXでグラフの交点を求めたときは,その座標を表示させたくなります.
MePoTeXの\sendMP内で使用した変数を\sendMPの外側で使用するには
次のようにします.
- 長さ等の数値変数(numeric)は「SaveNumeric(変数の列)」により保存する.
- 点の座標などのペア型変数(pair)は「SavePointName(変数の列)」により
保存する.
- 以上の保存を\sendMP内で終えた後に,\sendMP外では
「\UseNumeric(変数名)」として変数に保存されている値を利用する.
事前に保存されていれば、数値でも座標に対しても利用できる。
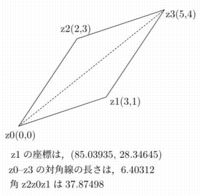
以下に,単純な例で試してみましょう.
下記では,点z1, z2をそれぞれ (3,1),(2,3) として,
これらを2辺とする平行四辺形の頂点(z3)を求めています.
-
\begin{MPpic}<1cm>(5,4)
\sendMP{
% 数値変数と座標
numeric naga,xx,yy,kaku[];
z1=(3w,h);z2=(2w,3h);
z0=origin;z3=z1+z2;
% 平行四辺形の描画
xdraw() z0--z1
--z3--z2--cycle;
xdraw(hasen()) z0--z3;
% z1の座標成分
xx=xpart(z1);
yy=ypart(z1);
% 対角線の長さ
naga=abs(z3)/28.34645;
% 角度
kaku1=angle(z1);
kaku2=angle(z2);
kaku3=kaku2-kaku1;
% 座標と数値の保存
SavePointName
(z0,z1,z2,z3);
SaveNumeric
(xx,yy,naga,kaku3);}
% 座標と値の表示
\mptLabel{z0}[c]
<-3mm,-3mm>
{z0\UseNumeric{z0}}
\mptLabel{z1}[tl]
<1mm,0mm>
{z1\UseNumeric{z1}}
\mptLabel{z2}[tl]
<-6mm,5mm>
{z2\UseNumeric{z2}}
\mptLabel{z3}[tl]
{z3\UseNumeric{z3}}
\mptLabel{(w,-h)}[c]
{z1の座標は,
(\UseNumeric{xx},
\UseNumeric{yy})}
\mptLabel{(1.5w,-1.5h)}[c]
{z0--z3の対角線の長さは,
\UseNumeric{naga}}
\mptLabel{(.6w,-2h)}[c]
{角z2z0z1は
\UseNumeric{kaku3}}
\end{MPpic}
-
|
上記では、幾つかの留意点があります。
- 最初に、数値変数を宣言します。
宣言時にx1、y1などを利用するとエラーになります。
数をつけて利用したいときは、kaku[]; のように [] を付記します。
これにより、kaku1, kuku2 などが使えます。
- 「abs」は絶対値関数で、
座標に対して使用すると長さ(\(\small \sqrt{x^2+y^2}\))になります。
- 「angle」は、その点の \(\small x\) 軸の正の方向からの角度を
度で返します。
- 点の名前は「SavePointName」、数値変数は「SaveNumeric」で
保存します。
- 長さは、pt数で計算されるようです。DTPでは
\(\small 1\,{\rm pt}=0.35277\cdots\,{\rm mm}\) なので、
\(\small 1\,{\rm cm}=28.34645\cdots\,{\rm pt}\) です。
cmに直すために28.34645で割っています。
- 座標を配置するとき、
その微妙な位置の調整には多少の試行錯誤が必要です。
- 座標として保存するときちんと表示されるようですが、
点(3,1)の座標を各成分に分けて数値変数として (xx, yy) で表示させると、
pt数で表示されます。したがって、
成分計算をした値を表示させるときは注意が必要です。
- 対角線の長さは \(\small \sqrt{25+16}=\sqrt{41}=6.40312\cdots\) です。
- \(\small \angle{z_2z_0z_1}\) は、内積の計算から
\[\small \begin{align*}
\cos\theta&=\frac{z_2\cdot z_1}{|z_2||z_1|}\\
&=\frac{6+3}{\sqrt{10}\,\sqrt{13}}\\
&=0.78935\cdots=t\\
\theta&=\cos^{-1}{t}\\
&=0.661043\cdots [{\rm rad}]\\
&=37.87498^{\circ}
\end{align*}
\]
|
|
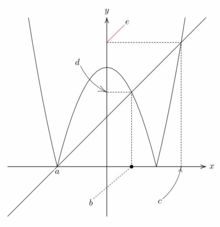
矢印つきラベル
|
座標軸上に値や記号を書き入れるとき、
その場所がグラフの近くにあるときは場所を離して書き入れたいものです。
そのようなとき、\mptLabelの
オプションの「dist, arcdir」等を利用すると、
軸上の場所を矢印で簡単に示すことができます。
-
\begin{MPpic}<1cm>
(4|4,6|2)
% 座標軸の描画
\mptXaxis[l]
<1mm,0mm>{$x$}
\mptYaxis[b]
<0mm,1mm>{$y$}
% グラフの描画
\sendMP{
z1=(-2w,0); z2=(w,0);
z3=(3w,0);z4=(0,3h);
z5=(0,5h);
xdraw() ClipPATH(kansu
(abs(t*t-4))(-4,4,40));
xdraw() kansu(t+2)(-4,4,10);
xdraw(hasen())
Pline(3w,5h);
xdraw(hasen())
Pline(1w,3h);}
\mptLabel{z1}[t]
<0mm,-1mm>{$a$}
\mptLabel{z2}[tr]
[dist=20mm*dir-140,
linetype=dashed hasen(),
arrowtype=-*]{$b$}
\mptLabel{z3}[r]
[dist=15mm*dir-120,
arcdir=-20,
arrowcurve=0.4,
arrowtype=->]
<0mm,-1mm>{$c$}
\mptLabel{z4}[br]
[dist=15mm*dir135,
arcdir=-20,
arrowlength=10pt,
arrowtype=->]
<0mm,0mm>{$d$}
\mptLabel{z5}[bl]
[dist=10mm*dir45,
linecolor=red]{$e$}
\end{MPpic}
-
|
上記では、5点を (-2,0), (1,0), (3,0), (0,3), (0,5)
として、いろいろなタイプの矢印で指定しています。
- 「linetype=」で、破線・点線を指定できます。
「dashed hasen()」または「dashed tensen()」とします。
- 「linecolor=」で、矢印の色を指定できます。
- 「dist=」で、矢印の長さと角度を指定します。
「dist=20mm*dir-140」では、
-140度の方向の20mm離れた箇所にラベルを配置します。
- 「arrowtype=」で、矢印の形式を指定できます。
種類としては、「->」「->>」「-*」「-o」(小文字のオー)、
「-|」などが指定でき、複数を組み合わせて「*->|」などと
することもできます。
- 「arcdir=」では、配置場所とラベルの位置との角度を指定できます。
- 「arrowlength=」では、やじりの長さを指定できます。
デフォルトは6ptです。
- 「arrowcurve=」では、やじりのそり具合を0〜0.5の数値で
指定できます。デフォルトは0.16です。
- 「arrowangle=」では、やじりの角度を指定できます。
デフォルトは40度です。
- 「angle=」で、ラベルの角度を変えられます。
|
減少加速関数
|
|
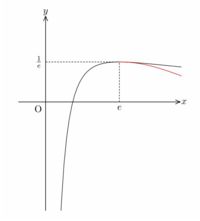
対数関数のように減少が遅すぎる関数に対して、
MePoTeXでは減少を加速してグラフを描画する機能があります。
\(\small x\geqq a\) の箇所での変化を加速するには「AccFun(a, 加速の度合い)(関数)」とします。
下図は、MePoTeXのマニュアルの図72(p.51)にある
\(\small \dfrac{\log{x}}{x}\) の場合です。
\(\small x\geqq e\) の箇所で減少が加速されています。
黒色のグラフがもともとのグラフです。
縦横の縮尺は変えています。赤色は、減少を加速させた場合です。
-
\begin{MPpic}<1cm,4cm>
(5|1,0.8|1)
% 座標軸
\mptXaxis<1mm,0mm>{$x$}
\mptYaxis<0mm,1mm>{$y$}
% グラフの描画
\sendMP{
z0=(exp1*w,h/exp1);
xdraw() ClipPATH
(kansu(ln(t)/t)
(0.2,5,50));
xdraw(hasen()) Pline(z0);
}
\mptLabel{origin}[tr]
<-1mm,-1mm>{O}
\mptLabel{(exp1*w,0)}[t]
<0mm,-1mm>{$e$}
\mptLabel{(0,h/exp1)}[r]
<-1mm,0mm>{$\frac1{e}$}
%
\sendMP{
xdraw(red) ClipPATH(
kansu(AccFun(exp1,0.8)
(ln t/t))(exp1,5,50));
}
\end{MPpic}
-
|
|
同様の形で、極大値と極小値が近いとき、その差を拡大して
描画するコマンド「DifFun」もあります。
詳しくはマニュアル(p.106)を参照してください。
|
|
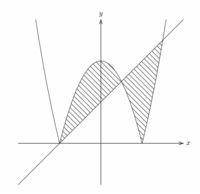
囲まれた領域
複数のグラフで囲まれた領域を色づけしたり斜線を引くには、
その閉じられた領域を指定する必要があります。
MetaPostには、閉じられた領域の周を検出する
「buildcycle」というマクロがあります。
-
\begin{MPpic}<1cm>(4|4,6|2)
% 座標軸の描画
\mptXaxis[l]
<1mm,0mm>{$x$}
\mptYaxis[b]
<0mm,1mm>{$y$}
% グラフの描画
\sendMP{
% パス変数の宣言と指定
path pth[];
pth0=kansu(abs(t*t-4))
(-4,4,40);
pth1=Linear(t+2);
% グラフ描画
xdraw() ClipPATH(pth0);
xdraw() pth1;
% 境界の取り出し
pth2=buildcycle(pth0,pth1);
% 斜線塗り
xfill(5pt*dir-45) pth2;
}
\end{MPpic}
-
|
|
ここでは、最初にパス変数を宣言します。
「path pth1, pth2;」とするとエラーになりますが、
「path pth[];」とすると、大丈夫のようです。
宣言の後は、pth0,pth1 などの数を入れて利用することができます。
複数のパス変数を「buildcycle」で指定すると、
MetaPostは自動的にその境界を抽出してくれます。
左側だけを抽出したいときは「subpath」を使用し、
「subpath(m,n) of pth0」のような形で使用します。
ここで「(m,n)」は、座標ではなく関数を定義するときの分割数から決まる値です。
上記の関数 \(\small |x^2-2|\) は \(\small -4\leqq x\leqq 4\) で定義され、
この区間を40等分しているので、1刻みは 0.2 です。
囲まれる領域の境い目の \(\small x=1\) が何番目に当たるかが重要です。
それは、簡単な計算から25番目であることが分かるので、
pht0の25番目までの部分とpth1とで囲まれる部分を抽出します。
-
\begin{MPpic}<1cm>(4|4,6|2)
% 座標軸の描画
\mptXaxis[l]<1mm,0mm>{$x$}
\mptYaxis[b]<0mm,1mm>{$y$}
% グラフの描画
\sendMP{
% パス変数の宣言と指定
path pth[];
pth0=kansu(abs(t*t-4))
(-4,4,40);
pth1=Linear(t+2);
% グラフ描画
xdraw() ClipPATH(pth0);
xdraw() pth1;
% 境界の取り出し
pth2=buildcycle
(subpath(0,25) of pth0,
pth1);
% 斜線塗り
xfill(5pt*dir-45) pth2;
}
\end{MPpic}
-
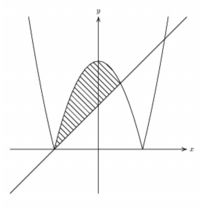
|
もう一つ別な例を示します.
2重積分などでは同心円で挟まれた領域を考える場合があります.
同心円は2つの曲線が交わらないので,「buildcyle」を利用することができません.
やむ得ないので,円上の点と進む方向を指定しながら,
ベジェー曲線で結んで
「cycle」を作って塗りつぶしました.
-
\begin{MPpic}<1cm>(3|3,3|3)
\mptXaxis[l]<1mm,0mm>{$x$}
\mptYaxis[b]<0mm,1mm>{$y$}
\mptPoint{z.O}[O][tr]
<-.1mm,-.1mm>{(0,0)}
\mptPoint{z.A}[$a$][tr]{(w,0)}
\mptPoint{z.B}[$b$][tl]{(2w,0)}
\sendMP{
path pth;
pth=(w,0){dir90}..(0,w){dir-180}
..(-w,0){dir-90}..(0,-w){dir0}
..(w,0){dir90}--(2w,0){dir-90}
..(0,-2w){dir-180}..(-2w,0){dir90}
..(0,2w){dir0}..(2w,0){dir-90}
--(w,0)--cycle;
xdraw() pth;
xfill(5pt*dir45) pth;}
\mptPoint{z.C}[$D$][tl]{(w,h)}
\end{MPpic}
-
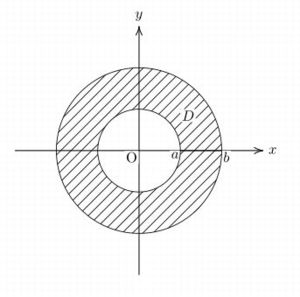
|
ただし、これはちょっと力技になってしまいます。
もっと単純に、外側の円全体を斜線塗りして、その後で
内側の円を白塗りする方が簡単です。
この場合は \(\small x\) 軸上の点を結んでいないので、
座標軸が濃くなる箇所はありません(図は略)。
-
\begin{MPpic}<1cm>(3|3,3|3)
\sendMP{
\path p,q;
p:=circle(origin,w);
q:=circle(origin,2w);
xfill(5pt*dir45) q;
xfill(white) p;
xdraw() p; xdraw() q; }
\mptXaxis[l]<1mm,0mm>{$x$}
\mptYaxis[b]<0mm,1mm>{$y$}
\mptPoint{z.O}[O][tr]
<-.2mm,-.2mm>{(0,0)}
\mptPoint{z.A}[$a$]
<-2mm,-2mm>{(w,0)}
\mptPoint{z.B}[$b$]
<2mm,-2mm>{(2w,0)}
\mptLabel{(w,h)}[tl]{$D$}
\end{MPpic}
|
|
図形の変形
特定の図形に対して、縦方向や横方向への拡大、平行移動、
原点の回りの回転、直線に関する対称移動を行うことができます。
まず、「fig」をパス変数としてして定義して、
関数のグラフや点を繋いだ経路を保存しておきます。
その上で、以下のような変形を行うことができます。
ペア型変数に対して行うと、ベクトルの変形として利用できます。
- fig scaled t
fig を原点を中心に t 倍する。
- fig xscaled t
fig を x 方向に t 倍する。
- fig yscaled t
fig を y 方向に t 倍する。
- fig shifted z
z はペア型変数とするとき、
fig を z だけ平行移動する。
- fig rotated t
fig を原点の回りに t 度回転する。
- fig rotatedaround (z,t)
fig を点 z の回りに t度回転する。
- fig reflectedabout (z1,z2)
2点 z1, z2 を結ぶ直線に関して、
fig を対称移動する。
-
\begin{MPpic}<1cm>(4|1,3|2)
% 格子と軸を描画
\mptDrawGrid
[linetype=dashed hasen()]
{-w step w until 4w}
{-2w step w until 3w}
\mptXaxis|-w==4w>
<1mm,0mm>{$x$}
\mptYaxis|-2w==3w>
<0mm,1mm>{$y$}
\sendMP{
path fig;
z0=origin; z1=(w,h);
fig=(0,0)--(w,0)
--(w,h)--cycle;
xfill(red) fig;
% いろいろな変形
xfill(green)
fig reflectedabout
(z0,z1);
xfill(blue)
fig rotated -90;
xdraw() fig xscaled 3;
xdraw() fig scaled 2;
xfill(Cyan) fig
shifted z1;
}
\end{MPpic}
-
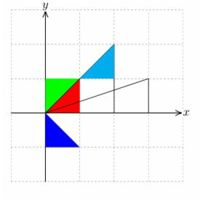
|
上記では、最初に「fig」をパス変数として宣言して
三角形を保存し、内部を赤で塗りつぶしています。
その後で、その三角形に対していろいろな変形を行っています。
緑色は (0,0)--(w,h) を含む直線に関して対称移動しています。
青色は 原点を中心に \(\small -90\)度回転しています。
枠線だけのものは、\(\small x\) 軸方向に3倍したものと、
原点を中心に2倍したものです。
シアン色は、z1=(w,h) だけ平行移動しています。
|
|
下記では、以上のことを関数 \(\small y=x^2-1\) のグラフに対して行っています。
-
\begin{MPpic}<1cm>
(4|4,4|4)
\mptDrawGrid
[linetype=dashed hasen()]
{-4w step w until 4w}
{-4w step w until 4w}
\mptXaxis|-4w==4w>
<1mm,0mm>{$x$}
\mptYaxis|-4w==4w>
<0mm,1mm>{$y$}
\sendMP{
path gra;
z1=(w,h); z2=(-w,h);
gra=kansu(t*t-1)(-4,4,40);
xdraw(1pt) ClipPATH(gra);
xdraw(Cyan,1pt)
ClipPATH(gra
shifted (-2w,0));
xdraw(hasen())
ClipPATH(gra xscaled 2);
xdraw(hasen(),red)
ClipPATH(gra scaled 1/2);
xdraw(green,1pt)
ClipPATH(gra
reflectedabout (z1,z2));
xdraw(blue,1pt)
ClipPATH(gra rotated 135);
}
\end{MPpic}
-
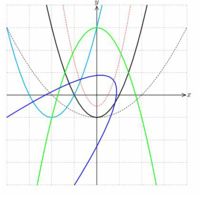
|
|
コードを見れば分かると思いますが、
シアン色は左に平行移動、黒の破線は \(\small x\) 方向に2倍し、
赤の破線は原点を中心に 1/2倍したものです。
緑色は直線 \(\small y=1\) に関して反転し、
青色は原点を中心に135度回転してます。
|
|
|
アフィン変換 |
■数学的な定義
アフィン変換は拡大・縮小や回転に加えて平行移動を含めた変換で、
その変換で点 \(\small (x,y)\) が点 \(\small (x',y')\) に移されたとすると、
2つの点の関係は
\[\small \begin{pmatrix}x'\\ y'\end{pmatrix}
=\begin{pmatrix}a&b\\ c&d\end{pmatrix}
\begin{pmatrix}x\\ y\end{pmatrix}+
\begin{pmatrix}e\\ f\end{pmatrix}
\]
で表されます。つまり、
アフィン変換は6つの成分 \(\small a,b,c,d,e,f\) で定義される変換です。
MetaPostでは、このような成分を持つ変数を「transform」で宣言します。
たとえば、「transform t;」とすると、\(\small t=(e,f,a,b,c,d)\)
という6つの成分からなります。\(\small (e,f)\) が最初にくることに注意して
ください。
■transform値の定め方
最初に \(\small t\) をtransform型変数として宣言したとしても、
たとえば \(\small t=(5,6,1,2,3,4)\) という形で定義することはできません。
その定め方には幾つかの方法があります。
原始的なやり方は、個々の成分を一つ一つ定義する方法です。
上述の式で \(\small a,b,c,d,e,f\) は、それぞれ \(\small t\) の
xxpart, xypart, yxpart, yypart, xpart,ypartで区別されます。
したがって、それぞれに具体的な値を定めることで \(\small t\) を定義することが
できます。
たとえば、直線 \(\small y=x\) に関して対称移動して \(\small (2,1)\) 方向に
平行移動する変換は
\[\small \begin{align*}
\begin{pmatrix}x'\\ y'\end{pmatrix}
&=\begin{pmatrix}0&1\\ 1&0\end{pmatrix}
\begin{pmatrix}x\\ y\end{pmatrix}+
\begin{pmatrix}2\\ 1\end{pmatrix}\\
&=\begin{pmatrix}y+2\\ x+1\end{pmatrix}
\end{align*}
\]
です。この場合は、\sendMP内で
xxpart=0; xypart=1; yxpart=1; yypart=0; xpart=2; ypart=1;
と定めることになります。
以上の定義は各成分を個別に定義するので面倒です。
MetaPostが連立1次方程式を解けることを利用すると、
各成分が満たす方程式で定義することができます。
どの点でもよいですが、(0,0), (1,0), (0,1) が
どこに移るかで指定するとよいでしょう。
それぞれ、(2,1), (2,2), (3,1)に移るので、この変換関係を
(2,1)=(0,0) transformed t;
(2,2)=(1,0) transformed t;
(3,1)=(0,1) transformed t;
と記述します。各成分ごとに式を書き出せば全部で6つの方程式になるので、
それを解くことで具体的な成分の値が分かります。
自分で解かなくてもMetaPostが解いてくれます。
「図形の変形」の箇所で述べた
変換を組み合わせた変換の場合は、
その組み合わせ方を記述することで定義することもできます。
上記で取り上げている変換は、z0=(0,0), z1=(w,h)とするとき、
z0, z1を通る直線に関して対称移動してから (2w,h) 方向に
平行移動することになるので、
t=identity reflectedabout (z0,z1) shifted (2w,h);
として定義することになります。「identity」は恒等変換です。
|
|
■アフィン変換の具体例
次に、以上のことを具体例でやってみましょう。
-
\begin{MPpic}<1cm>
(4|1,3|1)
\mptDrawGrid
[linetype=dashed hasen()]
{-w step w until 4w}
{-w step w until 3w}
\mptXaxis|-w==4w>
<1mm,0mm>{$x$}
\mptYaxis|-w==3w>
<0mm,1mm>{$y$}
\sendMP{
% 変数宣言
path fig,figt;
transform t;
% 点の定義
z0=origin; z1=(w,0);
z2=(w,h); z3=(2w,-h);
% transform値の定義
t=identity reflectedabout
(z0,z2) shifted (2w,h);
% 変換と描画
z4=z3 transformed t;
fig=z0--z1--z2--cycle;
xfill(red) fig;
figt=fig transformed t;
xfill(green) figt;
}
\mptPoint{z3}[P][bl]
(3pt){z3}
\mptPoint{z4}[Q][tr]
(3pt){z4}
\end{MPpic}
-
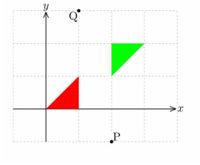
|
|
上記では、パス値としてfig, figtを宣言し、
transform値(t)を対称移動と平行移動で定義しています。
この変換で、赤の三角形が緑の三角形に変換されます。
念のため、点P(2w,-h)がどこに移ったかも例示しました。
|
|
|
パラパラ漫画 |
|
PDFのページを次々にめくっていくと、
アニメのように動いていく表現になります。
このような機能は「パラパラ漫画」と呼ばれていますが、
MePoTeXにはその機能を持つマクロが用意されています。
どのようなものであるかは、
パッケージの「parapara」フォルダーにある「spring.pdf」を
開いてみるとよいでしょう。
種類の異なるバネに繋がれた錘がどのような動きをするかが、
ページ送りの「→」を押し続けていると見えてきます。
パラパラ漫画のマクロは2種類がありますが、私の方で確認できたのは
MPpic環境を「\mptparapara」と「\repeat」で囲うマクロでした。
下記は単純な例ですが、
単位円を回転する点の縦の動きが正弦曲線を描くことを示したものです。
-
\begin{document}
% コマ数の指定
\mptparapara{36}
\begin{MPpic}<1cm>
(7|1.5,1.5|1.5)
% コマ数を n に取得
\mptgetkoma{n}
% 座標軸と格子の描画
(中略)
\sendMP{
numeric d,s,a;
d=PI/18; a=n+1;
s=d*a; ds=s*180/PI;
z0=origin;
z1=(s*w,sin(s)*h);
z2=(cos(s)*w,sin(s)*h);
% 正弦曲線
xdraw() kansu(sin(t))
(0,s,a);
% 単位円
xdraw(red) circulararc
(z0,(w,0),ds);
% 動径の描画
xdraw(red) z0--z2;
% 単位円と曲線の点を結ぶ
xdraw(hasen(),blue)
z1--z2;
}
\mptPoint{z1}(3pt){z1}
\mptPoint{z2}(3pt){z2}
\end{MPpic}
% 以上を繰り返す
\repeat
\end{document}
-
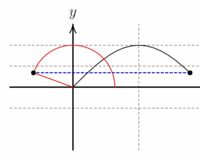
|
|
書式は、MPpic環境を「\mptparapara{コマ数}」と「\repeat」で
囲むだけです。
コマ数を指定して、その値を「\mptgetkoma」で指定する変数に受け取ります。
その後は、その変数を利用して、任意ページでの画像を作成します。
受け取った変数は、いったん「numeric」で宣言する別な数値変数に置き換えて、
置き換えた変数を利用した方が良いようです。私の場合、
\(\small n\) をそのまま利用したらエラーが生じました。
この値は、0から指定したコマ数まで変化します。
上記のコードは「0」の場合でも大丈夫だと思うのですが、
何度やってもエラーになるので、
出だしは「a=n+1」として「1」から始まるようにしています。
コードを見れば分かると思いますが、
「d=10度」刻みに曲線(z1)と単位円(z2)上の点の位置を求めています。
「s」は、\(\small n+1\)コマ目の \(\small x\) 座標、
「ds」は、そのときの角の大きさを度数法にしたものです。
単位円の円弧は「circulararc」を利用して、
中心と始点と角度を指定して描いています。
下記は、上記のコードで生成されたPDFファイルです。
ページ捲りの「→」を押し続けることでパラパラ漫画になります。
もう少し本格的なものが、
MePoTeXパッケージに
納められています。
2つのバネに繋がれて天井から吊された錘りの運動の様子を、
運動方程式からルンゲクッタ法による近似解を求めて、
「parapara」環境を利用して429ページのPDFとして生成されています。
ソースファイルは、MePoTeXのパッケージを解凍した
「parapara」フォルダーに納められています。
「ファイル(spring.pdf)」をダウンロードして、
ページ送りキーを押し続けてみて下さい。
ただし、ソースファイルをコンパイルすると、
コマ数の数だけMPSファイルが生成されるので、
コマ数が多いとファイルを置いてあるフォルダーがMPSだらけになります。
Ver4.50で追加されたマクロ「\mptSaveDir」
を利用すると,
このような画像ファイルを指定したフォルダーに納めるようにできます.
この機能を利用すると,有名な「
ローレンツアトラクター」もパラパラ漫画にすることができます.
|

